人教版数学九年级下册 第二十九章 章末复习 导学案
文档属性
| 名称 | 人教版数学九年级下册 第二十九章 章末复习 导学案 |  | |
| 格式 | doc | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 15:21:52 | ||
图片预览

文档简介
章末复习
一、诱导复习
1.课题导入
回顾本章所学知识,弄清其知识脉络,把握全章重点和考点.
2.复习目标
(1)能区分平行投影和中心投影.
(2)会画物体的三视图,也能由三视图想象实物的形状.
(3)能综合运用所学知识解决相关问题.
3.学习重、难点
重点:投影与三视图.
难点:知识的综合运用.
4.复习指导
(1)复习内容:教材P87~P111.
(2)复习时间:12分钟.
(3)复习方法:翻看课本,小组交流、研讨.
(4)复习参考提纲:
①如右图,地面A处有一根燃烧的蜡烛(高度不计),一个人在A与墙BC间运动,则他在墙上的投影的长度随他离墙的距离变小而 变小 (填“变大”“变小”或“不变”).
②已知线段AB的长为1 cm,投影面为P.
a.当AB平行于投影面P时,它的正投影A′B′的长是多少?
A′B′=1 cm.
b.当AB平行于投影面P时,将线段AB在垂直于P的平面内绕点A逆时针旋转30°,求这时AB的正投影A″B″的长度.
A″B″=AB×cos30°= (cm).
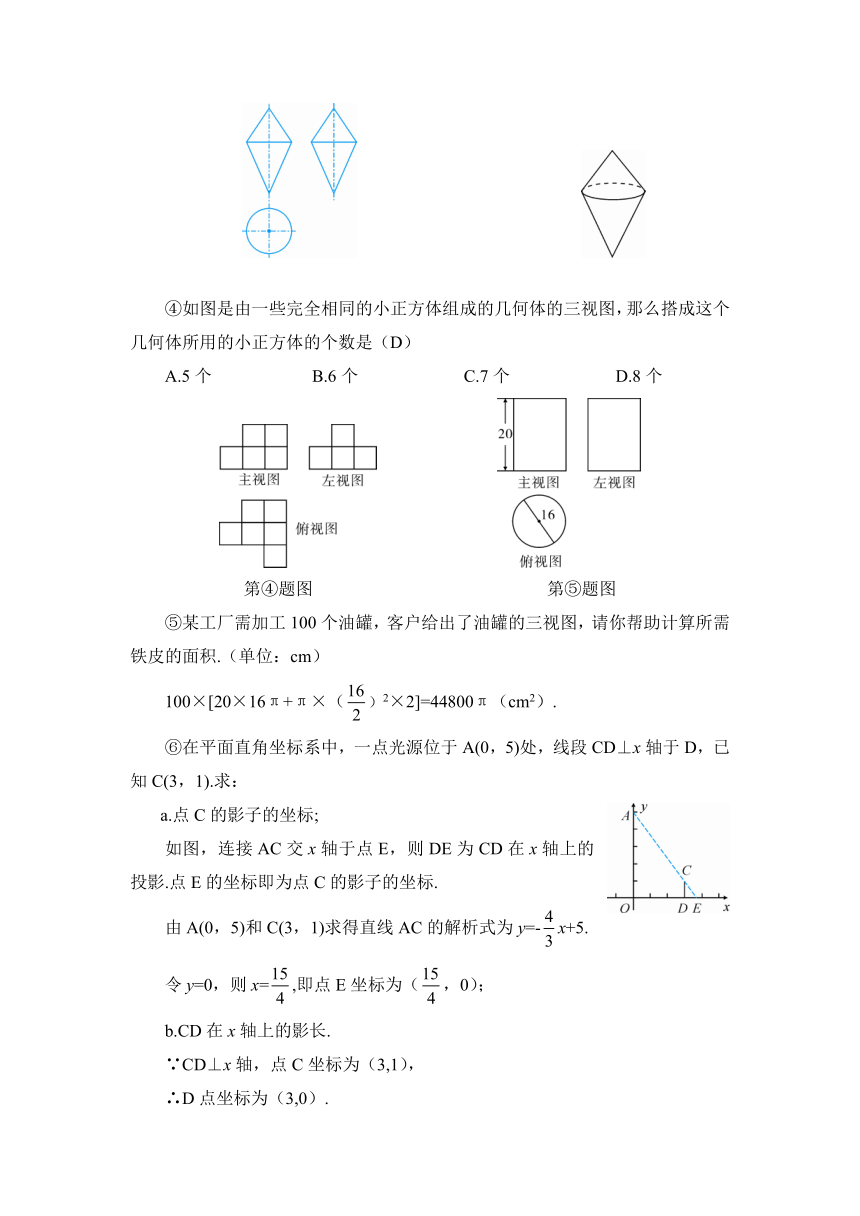
③如图是两个不同圆锥的组合体,请画出它的三视图.
④如图是由一些完全相同的小正方体组成的几何体的三视图,那么搭成这个几何体所用的小正方体的个数是(D)
A.5个 B.6个 C.7个 D.8个
第④题图 第⑤题图
⑤某工厂需加工100个油罐,客户给出了油罐的三视图,请你帮助计算所需铁皮的面积.(单位:cm)
100×[20×16π+π×()2×2]=44800π(cm2).
⑥在平面直角坐标系中,一点光源位于A(0,5)处,线段CD⊥x轴于D,已知C(3,1).求:
a.点C的影子的坐标;
如图,连接AC交x轴于点E,则DE为CD在x轴上的投影.点E的坐标即为点C的影子的坐标.
由A(0,5)和C(3,1)求得直线AC的解析式为y=-x+5.
令y=0,则x=,即点E坐标为(,0);
b.CD在x轴上的影长.
∵CD⊥x轴,点C坐标为(3,1),
∴D点坐标为(3,0).
∴DE=xE-xD=-3=.
即CD在x轴上的影长DE为.
二、自主复习
学生结合复习指导进行复习.
三、互助复习
1.师助生:
(1)明了学情:观察学生复习参考提纲的完成情况.
(2)差异指导:根据学情,对学困生进行个别指导或分类指导.
2.生助生:小组内相互交流、研讨、订正错误.
四、强化复习
展示交流复习成果.
五、评价
1.学生学习的自我评价:在这节课学习中,你有哪些新的认知?有哪些新的收获?对哪些内容还感到比较困难?
2.教师对学生的评价:
(1)表现性评价:点评学生学习的积极主动性、小组交流合作情况、学习效果和存在的问题等.
(2)纸笔评价:课堂评价检测.
3.教师的自我评价(教学反思).
本课时应帮助学生构建知识框图,精选典型例题进行讲解,力求让学生对本章知识了然于胸.教师在教学时应注意让学生在全面掌握知识点的基础上抓住重点,能够举一反三.
一、基础巩固(70分)
1.(10分)下列投影中是正投影的是(C)
A B C D
2.(10分)一个正方体的表面展开图如图所示,每个面内都标注了字母,如果从正方体的右面看是面D,面C在后面,则正方体的上面是(A)
A.面E B.面F C.面A D.面B
3.(10分)图中三视图所对应的几何体是 (3) .(填序号)
4.(20分)分别画出下列几何体的三视图.
解:
5.(20分)根据三视图描述物体的形状.
解:图1描述的物体为正六棱柱;图2描述的物体为由6个同样大小的正方体呈阶梯形排成一排的几何体.
二、综合应用(20分)
6.(20分)根据下列三视图,求它们表示的几何体的体积.(单位:cm)
解:(1)2×π×()2+8×π×()2=136π(cm3).
(2)6×4×2+π×22×2÷2=(48+4π)(cm3).
三、拓展延伸(10分)
7.(10分)如图是一个几何体的三视图.(单位:cm)
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.(保留根号)
解:(1)圆锥;
(2)π×()2+×4π×6=16π(cm2).
(3)圆锥的侧面展开图如下图所示,最短线路为线段BD.
设∠BAC=n°,则×6=4π,解得n=60.
即∠BAC=60°.连BC,则△ABC是等边三角形.
∵D为AC的中点,∴BD⊥AC,即△ABD是直角三角形.
∴BD=3 (cm).
∴最短路程为3 cm.
一、诱导复习
1.课题导入
回顾本章所学知识,弄清其知识脉络,把握全章重点和考点.
2.复习目标
(1)能区分平行投影和中心投影.
(2)会画物体的三视图,也能由三视图想象实物的形状.
(3)能综合运用所学知识解决相关问题.
3.学习重、难点
重点:投影与三视图.
难点:知识的综合运用.
4.复习指导
(1)复习内容:教材P87~P111.
(2)复习时间:12分钟.
(3)复习方法:翻看课本,小组交流、研讨.
(4)复习参考提纲:
①如右图,地面A处有一根燃烧的蜡烛(高度不计),一个人在A与墙BC间运动,则他在墙上的投影的长度随他离墙的距离变小而 变小 (填“变大”“变小”或“不变”).
②已知线段AB的长为1 cm,投影面为P.
a.当AB平行于投影面P时,它的正投影A′B′的长是多少?
A′B′=1 cm.
b.当AB平行于投影面P时,将线段AB在垂直于P的平面内绕点A逆时针旋转30°,求这时AB的正投影A″B″的长度.
A″B″=AB×cos30°= (cm).
③如图是两个不同圆锥的组合体,请画出它的三视图.
④如图是由一些完全相同的小正方体组成的几何体的三视图,那么搭成这个几何体所用的小正方体的个数是(D)
A.5个 B.6个 C.7个 D.8个
第④题图 第⑤题图
⑤某工厂需加工100个油罐,客户给出了油罐的三视图,请你帮助计算所需铁皮的面积.(单位:cm)
100×[20×16π+π×()2×2]=44800π(cm2).
⑥在平面直角坐标系中,一点光源位于A(0,5)处,线段CD⊥x轴于D,已知C(3,1).求:
a.点C的影子的坐标;
如图,连接AC交x轴于点E,则DE为CD在x轴上的投影.点E的坐标即为点C的影子的坐标.
由A(0,5)和C(3,1)求得直线AC的解析式为y=-x+5.
令y=0,则x=,即点E坐标为(,0);
b.CD在x轴上的影长.
∵CD⊥x轴,点C坐标为(3,1),
∴D点坐标为(3,0).
∴DE=xE-xD=-3=.
即CD在x轴上的影长DE为.
二、自主复习
学生结合复习指导进行复习.
三、互助复习
1.师助生:
(1)明了学情:观察学生复习参考提纲的完成情况.
(2)差异指导:根据学情,对学困生进行个别指导或分类指导.
2.生助生:小组内相互交流、研讨、订正错误.
四、强化复习
展示交流复习成果.
五、评价
1.学生学习的自我评价:在这节课学习中,你有哪些新的认知?有哪些新的收获?对哪些内容还感到比较困难?
2.教师对学生的评价:
(1)表现性评价:点评学生学习的积极主动性、小组交流合作情况、学习效果和存在的问题等.
(2)纸笔评价:课堂评价检测.
3.教师的自我评价(教学反思).
本课时应帮助学生构建知识框图,精选典型例题进行讲解,力求让学生对本章知识了然于胸.教师在教学时应注意让学生在全面掌握知识点的基础上抓住重点,能够举一反三.
一、基础巩固(70分)
1.(10分)下列投影中是正投影的是(C)
A B C D
2.(10分)一个正方体的表面展开图如图所示,每个面内都标注了字母,如果从正方体的右面看是面D,面C在后面,则正方体的上面是(A)
A.面E B.面F C.面A D.面B
3.(10分)图中三视图所对应的几何体是 (3) .(填序号)
4.(20分)分别画出下列几何体的三视图.
解:
5.(20分)根据三视图描述物体的形状.
解:图1描述的物体为正六棱柱;图2描述的物体为由6个同样大小的正方体呈阶梯形排成一排的几何体.
二、综合应用(20分)
6.(20分)根据下列三视图,求它们表示的几何体的体积.(单位:cm)
解:(1)2×π×()2+8×π×()2=136π(cm3).
(2)6×4×2+π×22×2÷2=(48+4π)(cm3).
三、拓展延伸(10分)
7.(10分)如图是一个几何体的三视图.(单位:cm)
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.(保留根号)
解:(1)圆锥;
(2)π×()2+×4π×6=16π(cm2).
(3)圆锥的侧面展开图如下图所示,最短线路为线段BD.
设∠BAC=n°,则×6=4π,解得n=60.
即∠BAC=60°.连BC,则△ABC是等边三角形.
∵D为AC的中点,∴BD⊥AC,即△ABD是直角三角形.
∴BD=3 (cm).
∴最短路程为3 cm.
