华师大版数学七年级下册 第9章多边形9.1.1认识三角形(第2课时)教案
文档属性
| 名称 | 华师大版数学七年级下册 第9章多边形9.1.1认识三角形(第2课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览

文档简介
第9章 多边形
9.1 三角形
9.1.1 认识三角形
第2课时 三角形中的重要线段
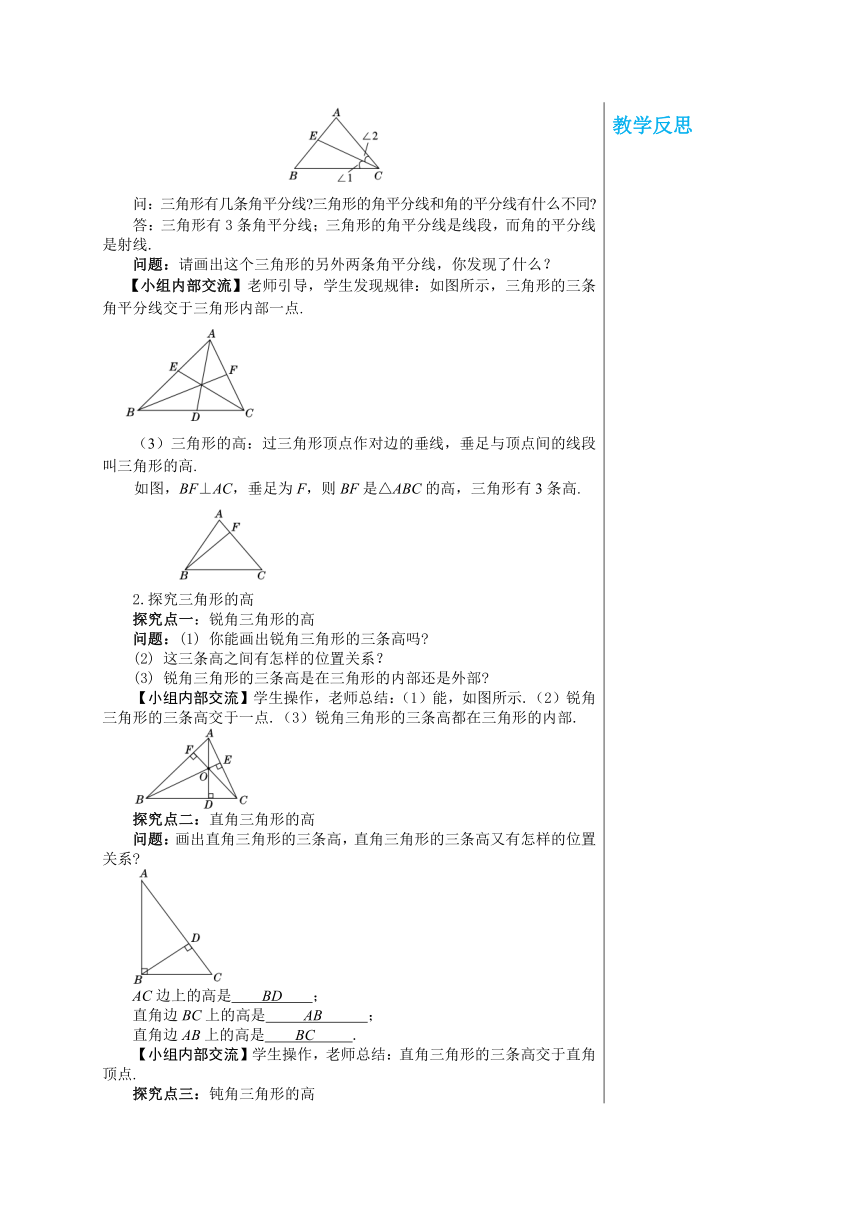
教学目标 1.掌握三角形的高、中线、角平分线的定义中体现出来的性质. 2.会画三角形的高、中线、角平分线. 教学重难点 重点:了解三角形的高、中线、角平分线的概念,会用工具准确画出三角形的高、中线、角平分线. 难点:掌握钝角三角形高的画法. 教学过程 导入新课 1.过直线外一点,画已知直线的垂线,能画几条?怎么画? 2.已知△ABC中,BC5 cm,高AD4 cm,求△ABC的面积. 探究新知 合作探究 1.三角形中的三种重要线段——中线、角平分线和高. (1)三角形的中线:三角形的一个顶点与它的对边中点的连线叫三角形的中线.如图,点D是BC边的中点,即AD是△ABC的中线. 问:三角形有几条中线 若已知AD是三角形的中线,你可得到什么结论 (三角形有3条中线,若已知AD是三角形的中线,得到结论BDCD BC,S△ACDS△ABD) 操作:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,观察它们中线的交点,你会发现什么规律? 【分组动手操作】老师引导,学生发现规律:三角形的三条中线交于三角形内部一点. (2)三角形的角平分线:三角形内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线. 如图,∠1=∠2,那么CE是△ABC的角平分线. 问:三角形有几条角平分线 三角形的角平分线和角的平分线有什么不同 答:三角形有3条角平分线;三角形的角平分线是线段,而角的平分线是射线. 问题:请画出这个三角形的另外两条角平分线,你发现了什么? 【小组内部交流】老师引导,学生发现规律:如图所示,三角形的三条角平分线交于三角形内部一点. (3)三角形的高:过三角形顶点作对边的垂线,垂足与顶点间的线段叫三角形的高. 如图,BF⊥AC,垂足为F,则BF是△ABC的高,三角形有3条高. 2.探究三角形的高 探究点一:锐角三角形的高 问题:(1) 你能画出锐角三角形的三条高吗 (2) 这三条高之间有怎样的位置关系? (3) 锐角三角形的三条高是在三角形的内部还是外部 【小组内部交流】学生操作,老师总结:(1)能,如图所示.(2)锐角三角形的三条高交于一点.(3)锐角三角形的三条高都在三角形的内部. 探究点二:直角三角形的高 问题:画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系 AC边上的高是 BD ; 直角边BC上的高是 AB ; 直角边AB上的高是 BC . 【小组内部交流】学生操作,老师总结:直角三角形的三条高交于直角顶点. 探究点三:钝角三角形的高 问题:画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系 【小组内部交流】学生操作,老师总结:如图所示,钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于三角形外一点. 课堂练习 1.下列四个图形中,线段BE是△ABC的高的图形是( ) A. B. C. D. 2.用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( ) A. B. C. D. 3.下列说法错误的是( ) A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线都在三角形内部 C.锐角三角形的三条高一定交于同一点 D.三角形的三条高、三条中线、三条角平分线都交于同一点 4.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形. 5.如图所示,BD是△ABC的中线,AD2,AB+BC5,求△ABC的周长. 参考答案 1.A 2.B 3.D 4.直角 5.解:因为BD是△ABC的中线, 所以点D是AC的中点, 所以AC2AD4, 所以△ABC的周长为AB+BC+AC5+49. 课堂小结 1.三角形的三种重要线段——中线、高、角平分线的概念. 2.三角形的中线、高、角平分线的画法. 三角形的三条中线(高、角平分线)之间的位置关系以及它们与三角形间的位置关系. 布置作业 课本第76页练习. 板书设计 第9章 多边形 9.1 三角形 9.1.1 认识三角形 第2课时 三角形中的重要线段 1.三角形中的三种重要线段——中线、角平分线和高. 2.锐角三角形、直角三角形、钝角三角形的高. 教学反思 教学反思 教学反思 教学反思
9.1 三角形
9.1.1 认识三角形
第2课时 三角形中的重要线段
教学目标 1.掌握三角形的高、中线、角平分线的定义中体现出来的性质. 2.会画三角形的高、中线、角平分线. 教学重难点 重点:了解三角形的高、中线、角平分线的概念,会用工具准确画出三角形的高、中线、角平分线. 难点:掌握钝角三角形高的画法. 教学过程 导入新课 1.过直线外一点,画已知直线的垂线,能画几条?怎么画? 2.已知△ABC中,BC5 cm,高AD4 cm,求△ABC的面积. 探究新知 合作探究 1.三角形中的三种重要线段——中线、角平分线和高. (1)三角形的中线:三角形的一个顶点与它的对边中点的连线叫三角形的中线.如图,点D是BC边的中点,即AD是△ABC的中线. 问:三角形有几条中线 若已知AD是三角形的中线,你可得到什么结论 (三角形有3条中线,若已知AD是三角形的中线,得到结论BDCD BC,S△ACDS△ABD) 操作:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,观察它们中线的交点,你会发现什么规律? 【分组动手操作】老师引导,学生发现规律:三角形的三条中线交于三角形内部一点. (2)三角形的角平分线:三角形内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线. 如图,∠1=∠2,那么CE是△ABC的角平分线. 问:三角形有几条角平分线 三角形的角平分线和角的平分线有什么不同 答:三角形有3条角平分线;三角形的角平分线是线段,而角的平分线是射线. 问题:请画出这个三角形的另外两条角平分线,你发现了什么? 【小组内部交流】老师引导,学生发现规律:如图所示,三角形的三条角平分线交于三角形内部一点. (3)三角形的高:过三角形顶点作对边的垂线,垂足与顶点间的线段叫三角形的高. 如图,BF⊥AC,垂足为F,则BF是△ABC的高,三角形有3条高. 2.探究三角形的高 探究点一:锐角三角形的高 问题:(1) 你能画出锐角三角形的三条高吗 (2) 这三条高之间有怎样的位置关系? (3) 锐角三角形的三条高是在三角形的内部还是外部 【小组内部交流】学生操作,老师总结:(1)能,如图所示.(2)锐角三角形的三条高交于一点.(3)锐角三角形的三条高都在三角形的内部. 探究点二:直角三角形的高 问题:画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系 AC边上的高是 BD ; 直角边BC上的高是 AB ; 直角边AB上的高是 BC . 【小组内部交流】学生操作,老师总结:直角三角形的三条高交于直角顶点. 探究点三:钝角三角形的高 问题:画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系 【小组内部交流】学生操作,老师总结:如图所示,钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于三角形外一点. 课堂练习 1.下列四个图形中,线段BE是△ABC的高的图形是( ) A. B. C. D. 2.用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( ) A. B. C. D. 3.下列说法错误的是( ) A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线都在三角形内部 C.锐角三角形的三条高一定交于同一点 D.三角形的三条高、三条中线、三条角平分线都交于同一点 4.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形. 5.如图所示,BD是△ABC的中线,AD2,AB+BC5,求△ABC的周长. 参考答案 1.A 2.B 3.D 4.直角 5.解:因为BD是△ABC的中线, 所以点D是AC的中点, 所以AC2AD4, 所以△ABC的周长为AB+BC+AC5+49. 课堂小结 1.三角形的三种重要线段——中线、高、角平分线的概念. 2.三角形的中线、高、角平分线的画法. 三角形的三条中线(高、角平分线)之间的位置关系以及它们与三角形间的位置关系. 布置作业 课本第76页练习. 板书设计 第9章 多边形 9.1 三角形 9.1.1 认识三角形 第2课时 三角形中的重要线段 1.三角形中的三种重要线段——中线、角平分线和高. 2.锐角三角形、直角三角形、钝角三角形的高. 教学反思 教学反思 教学反思 教学反思
