19.2.2菱形(1)学案
文档属性
| 名称 | 19.2.2菱形(1)学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-24 00:36:21 | ||
图片预览

文档简介
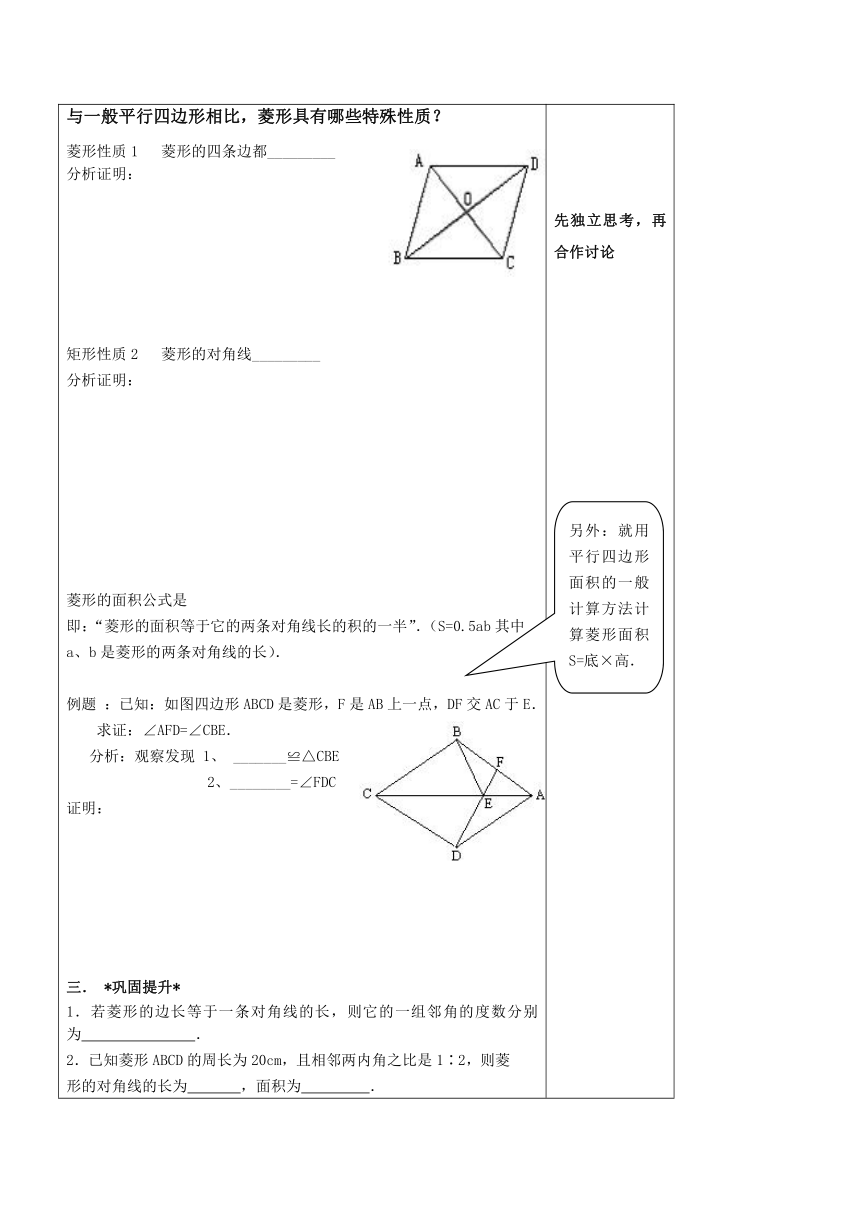
学科:数学 年级:八年级 主备人: 审核人: 课题:菱形(一) 课型:预习+展示 小主人姓名:
*学习目标*:1、理解并掌握菱形的定义及性质。2、会用这些性质进行有关的论证和计算,会计算菱形的面积。*学习重点*:菱形的性质 。*学习难点*:菱形的性质及菱形知识的综合应用。
学习过程 学法指导
一。*能力生成*活动一1、什么叫做平行四边形?什么叫矩形?平行四边形和矩形之间的关系是什么?2.(引入)我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形菱形。_______________ 的平行四边形是菱形活动二 见课本第97页【探究】菱形的性质,可以动手利用折纸、剪切的方法,探究、归纳. 【强调】 菱形定义(1)是平行四边形;(2)一组邻边相等.
与一般平行四边形相比,菱形具有哪些特殊性质?菱形性质1 菱形的四条边都_________分析证明:矩形性质2 菱形的对角线_________分析证明:菱形的面积公式是 即:“菱形的面积等于它的两条对角线长的积的一半”.(S=0.5ab其中a、b是菱形的两条对角线的长).例题 :已知:如图四边形ABCD是菱形,F是AB上一点,DF交AC于E. 求证:∠AFD=∠CBE. 分析:观察发现 1、 _______≌△CBE 2、________=∠FDC证明: *巩固提升*1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .2.已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,则菱形的对角线的长为 ,面积为 .3. 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH. 四.*检测反馈*1.下列图形中,即是中心对称图形又是轴对称图形的是 ( )A.等边三角形 B.菱形 C.等腰梯形 D.平行四边形2.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )A.20 B.15 C.10 D.53.(09南宁)如图2,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )A.10cm2 B.20cm2 C.40cm2 D.80cm第3题图 第5题图 第6题图4.菱形的两条对角线长分别为6和8,则它的面积为________,周长为_________。5.(09杭州)如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( ) A.35° B.45° C.50° D.55°6.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,求∠CED的度数。 先独立思考,再合作讨论菱形的边和对角线有不同于一般的平行四边形的性质,有关菱形的几何计算问题可以化为直角三角形、等腰三角形),利用特殊三角形的性质来计算。即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
A
B
E
F
C
D
A
D
E
P
C
B
F
另外:就用平行四边形面积的一般计算方法计算菱形面积S=底×高.
*学习目标*:1、理解并掌握菱形的定义及性质。2、会用这些性质进行有关的论证和计算,会计算菱形的面积。*学习重点*:菱形的性质 。*学习难点*:菱形的性质及菱形知识的综合应用。
学习过程 学法指导
一。*能力生成*活动一1、什么叫做平行四边形?什么叫矩形?平行四边形和矩形之间的关系是什么?2.(引入)我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形菱形。_______________ 的平行四边形是菱形活动二 见课本第97页【探究】菱形的性质,可以动手利用折纸、剪切的方法,探究、归纳. 【强调】 菱形定义(1)是平行四边形;(2)一组邻边相等.
与一般平行四边形相比,菱形具有哪些特殊性质?菱形性质1 菱形的四条边都_________分析证明:矩形性质2 菱形的对角线_________分析证明:菱形的面积公式是 即:“菱形的面积等于它的两条对角线长的积的一半”.(S=0.5ab其中a、b是菱形的两条对角线的长).例题 :已知:如图四边形ABCD是菱形,F是AB上一点,DF交AC于E. 求证:∠AFD=∠CBE. 分析:观察发现 1、 _______≌△CBE 2、________=∠FDC证明: *巩固提升*1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .2.已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,则菱形的对角线的长为 ,面积为 .3. 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH. 四.*检测反馈*1.下列图形中,即是中心对称图形又是轴对称图形的是 ( )A.等边三角形 B.菱形 C.等腰梯形 D.平行四边形2.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )A.20 B.15 C.10 D.53.(09南宁)如图2,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )A.10cm2 B.20cm2 C.40cm2 D.80cm第3题图 第5题图 第6题图4.菱形的两条对角线长分别为6和8,则它的面积为________,周长为_________。5.(09杭州)如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( ) A.35° B.45° C.50° D.55°6.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,求∠CED的度数。 先独立思考,再合作讨论菱形的边和对角线有不同于一般的平行四边形的性质,有关菱形的几何计算问题可以化为直角三角形、等腰三角形),利用特殊三角形的性质来计算。即学即练一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
A
B
E
F
C
D
A
D
E
P
C
B
F
另外:就用平行四边形面积的一般计算方法计算菱形面积S=底×高.
