19.2.2菱形的判定学案
文档属性
| 名称 | 19.2.2菱形的判定学案 | 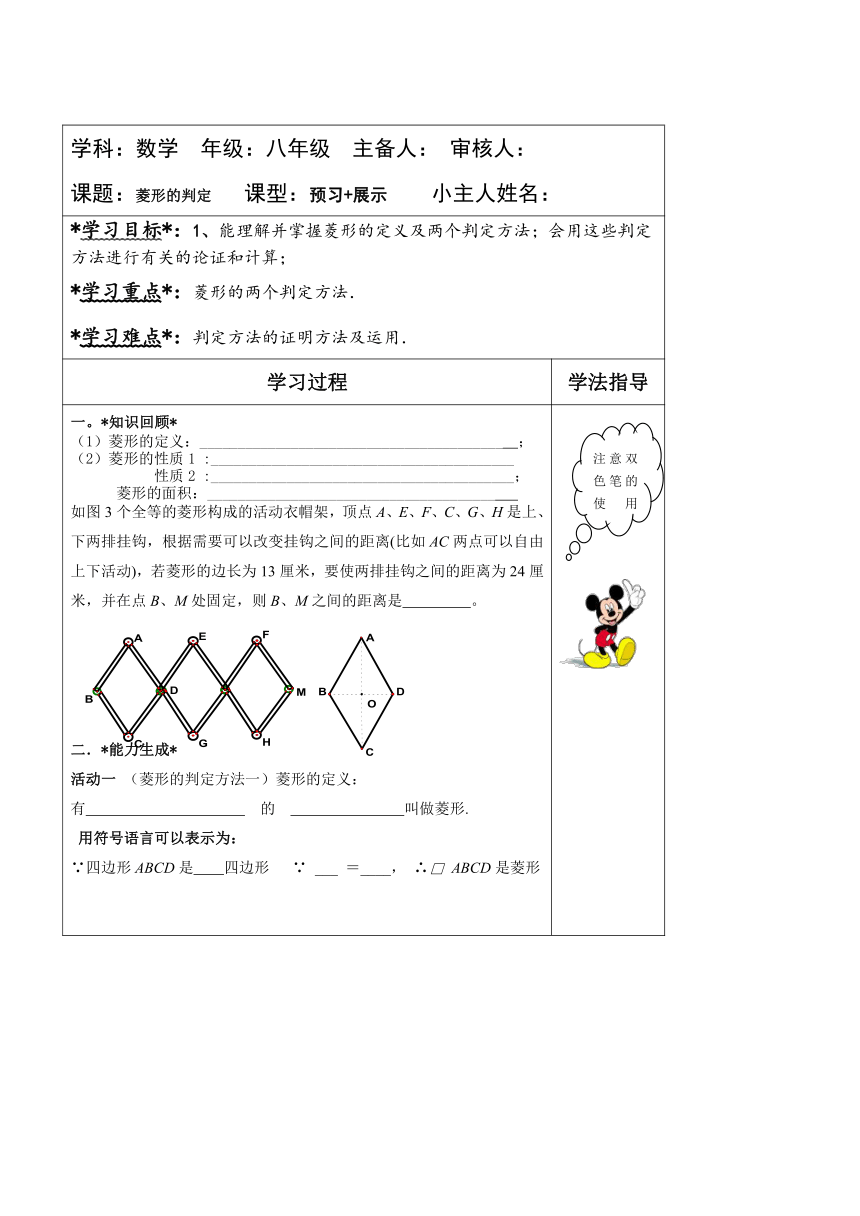 | |
| 格式 | zip | ||
| 文件大小 | 95.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-24 00:37:31 | ||
图片预览


文档简介
学科:数学 年级:八年级 主备人: 审核人: 课题:菱形的判定 课型:预习+展示 小主人姓名:
*学习目标*:1、能理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;*学习重点*:菱形的两个判定方法.*学习难点*:判定方法的证明方法及运用.
学习过程 学法指导
一。*知识回顾*(1)菱形的定义:________________________________________ ; (2)菱形的性质1 :________________________________________ 性质2 :________________________________________;菱形的面积:______________________________________ 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是 。 二.*能力生成*活动一 (菱形的判定方法一)菱形的定义:有 的 叫做菱形.用符号语言可以表示为:∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
例 :如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点. 求证:(1)四边形AEDF是平行四边形 (2)∠2﹦∠3 (3)四边形AEDF是菱形活动二:探究并掌握菱形的判定方法二1.( 画图)自学99页最后三行的画图过程,用圆规画出菱形ABCD,图画在右边(保留作图痕迹)2.你发现四边形ABCD四边的关系是: 3.(猜想)四边相等的四边形ABCD是一个_____形.4.(证明)利用上图证明:“四边相等的四边形是菱形”已知:如上图,在四边形_______中,____=____=____=____求证:四边形ABCD是_____.证明:由上写出菱形的判定方法二:_______ . 利用上图用符号语言表示为:在四边形ABCD中, ∵ ____=____=____=____ ∴四边形ABCD是 形活动三 菱形的判定方法三阅读99页“探究”,利用自制的学具探究菱形的判定方法并完成下面各题1.由“在一长一短的木条中点处固定一个小钉”可知: = , = ∴四边形ABCD是 四边形2.转动十字,当∠_____= °时即___ ⊥ ___时,四边形变成了菱形. 3. (猜想)对角线互相____ 的平行四边形是菱形.请利用下图证明你的猜想:已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形. 4.总结写出菱形判定方法三: 利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,且AC___BD,∴□ABCD是菱形*巩固提升*1、下列条件中,能判定四边形是菱形的是 ( ).(A)两条对角线相等 (B)两条对角线互相垂直(C)两条对角线相等且互相垂直 (D)两条对角线互相垂直平分2、自学99页例三完成下题“在□ABCD中,对角线AC和BD相交于点O,并且AB=9,OB=6,OA=3.求证:(1)AC⊥BD (2)□ABCD是菱形吗?说说你的理由. (3)求四边形ABCD的面积. 四.*检测反馈*1、判断题,对的画“√”错的画“×”(1).对角线互相垂直的四边形是菱形( )(2).一条对角线垂直另一条对角线的四边形是菱形( )(3)..对角线互相垂直且平分的四边形是菱形( )(4).对角线相等的四边形是菱形( )2、如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:(1)四边形ABCD是平行四边形(2) 过A作AE⊥BC于E点, 过A作AF⊥CD于F.用等积法说明BC=CD.(3) 求证:四边形ABCD是菱形. 3. 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.五.*课堂小结*菱形的判定方法菱形的判定应具备的条件菱形的定义判定定理1判定定理2 先独立思考,再合作讨论菱形常用的判定方法归纳为 注意:判定对象分别为四边形和平行四边形即学即练等积法:指图形的面积相等一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
*学习目标*:1、能理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;*学习重点*:菱形的两个判定方法.*学习难点*:判定方法的证明方法及运用.
学习过程 学法指导
一。*知识回顾*(1)菱形的定义:________________________________________ ; (2)菱形的性质1 :________________________________________ 性质2 :________________________________________;菱形的面积:______________________________________ 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是 。 二.*能力生成*活动一 (菱形的判定方法一)菱形的定义:有 的 叫做菱形.用符号语言可以表示为:∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
例 :如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点. 求证:(1)四边形AEDF是平行四边形 (2)∠2﹦∠3 (3)四边形AEDF是菱形活动二:探究并掌握菱形的判定方法二1.( 画图)自学99页最后三行的画图过程,用圆规画出菱形ABCD,图画在右边(保留作图痕迹)2.你发现四边形ABCD四边的关系是: 3.(猜想)四边相等的四边形ABCD是一个_____形.4.(证明)利用上图证明:“四边相等的四边形是菱形”已知:如上图,在四边形_______中,____=____=____=____求证:四边形ABCD是_____.证明:由上写出菱形的判定方法二:_______ . 利用上图用符号语言表示为:在四边形ABCD中, ∵ ____=____=____=____ ∴四边形ABCD是 形活动三 菱形的判定方法三阅读99页“探究”,利用自制的学具探究菱形的判定方法并完成下面各题1.由“在一长一短的木条中点处固定一个小钉”可知: = , = ∴四边形ABCD是 四边形2.转动十字,当∠_____= °时即___ ⊥ ___时,四边形变成了菱形. 3. (猜想)对角线互相____ 的平行四边形是菱形.请利用下图证明你的猜想:已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形. 4.总结写出菱形判定方法三: 利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,且AC___BD,∴□ABCD是菱形*巩固提升*1、下列条件中,能判定四边形是菱形的是 ( ).(A)两条对角线相等 (B)两条对角线互相垂直(C)两条对角线相等且互相垂直 (D)两条对角线互相垂直平分2、自学99页例三完成下题“在□ABCD中,对角线AC和BD相交于点O,并且AB=9,OB=6,OA=3.求证:(1)AC⊥BD (2)□ABCD是菱形吗?说说你的理由. (3)求四边形ABCD的面积. 四.*检测反馈*1、判断题,对的画“√”错的画“×”(1).对角线互相垂直的四边形是菱形( )(2).一条对角线垂直另一条对角线的四边形是菱形( )(3)..对角线互相垂直且平分的四边形是菱形( )(4).对角线相等的四边形是菱形( )2、如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:(1)四边形ABCD是平行四边形(2) 过A作AE⊥BC于E点, 过A作AF⊥CD于F.用等积法说明BC=CD.(3) 求证:四边形ABCD是菱形. 3. 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.五.*课堂小结*菱形的判定方法菱形的判定应具备的条件菱形的定义判定定理1判定定理2 先独立思考,再合作讨论菱形常用的判定方法归纳为 注意:判定对象分别为四边形和平行四边形即学即练等积法:指图形的面积相等一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
