北师大版数学七年级上册同步课时练习:5.3 应用一元一次方程——水箱变高了(word版含答案)
文档属性
| 名称 | 北师大版数学七年级上册同步课时练习:5.3 应用一元一次方程——水箱变高了(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 17:27:16 | ||
图片预览



文档简介
3 应用一元一次方程——水箱变高了
知识点 1 等积变形问题
1.已知底面半径为5 cm、高为7 cm的圆柱体的体积是底面直径为4 cm、高为x cm的圆柱体的体积的5倍,则下列方程正确的是( )
A.5π×42x=π×102×7
B.π×42x=5π×102×7
C.5π×2x=π×2×7
D.5π×2x=π×52×7
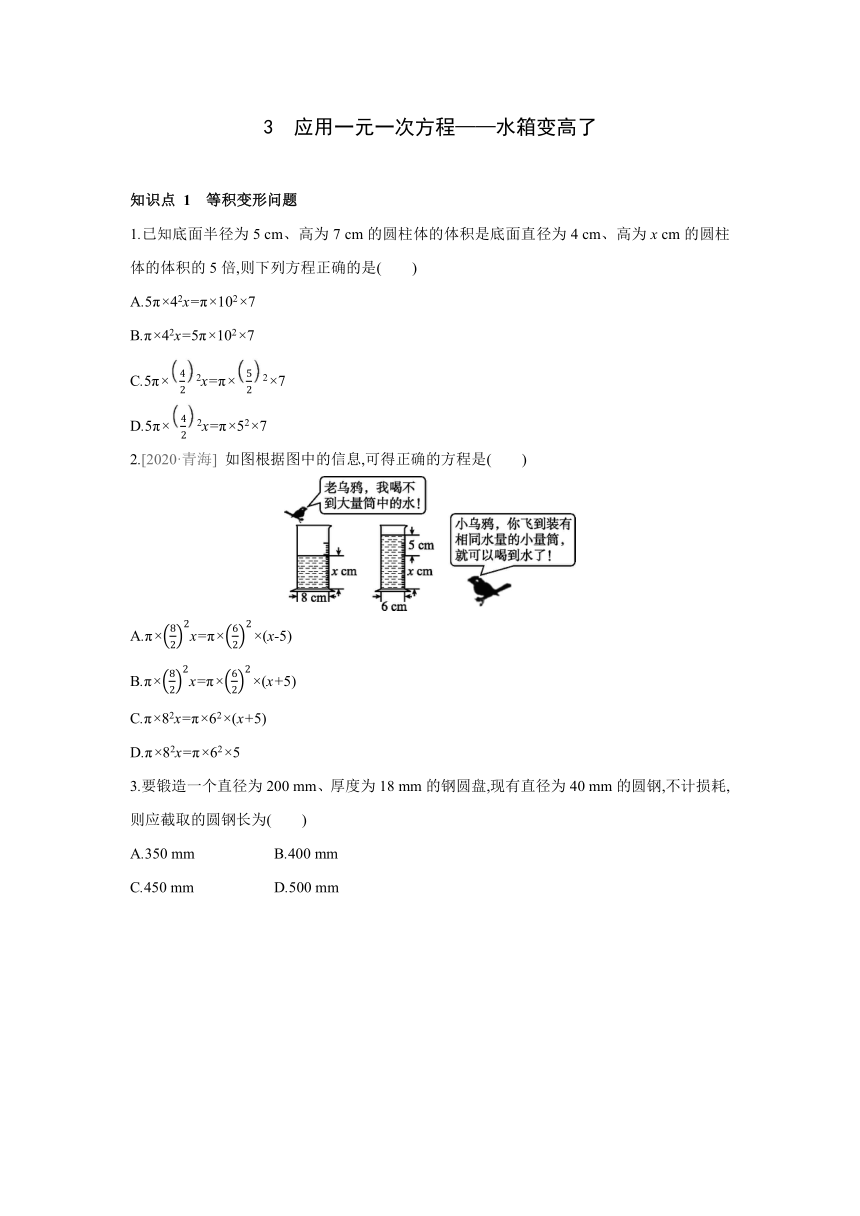
2.[2020·青海] 如图根据图中的信息,可得正确的方程是( )
A.π×x=π××(x-5)
B.π×x=π××(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
3.要锻造一个直径为200 mm、厚度为18 mm的钢圆盘,现有直径为40 mm的圆钢,不计损耗,则应截取的圆钢长为( )
A.350 mm B.400 mm
C.450 mm D.500 mm
4.如图用直径为200 mm的圆钢锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯底板,应截取多长的圆钢
5.如图一圆柱形容器的底面半径为0.5 m,高为1.5 m,里面盛有1 m深的水,将底面半径为0.3 m、高为0.5 m的圆柱形铁块沉入水中,则容器内水面将升高多少米
知识点 2 根据周长、面积列方程
6.一块长方形草坪的长比宽多10 m,它的周长是132 m,求该长方形草坪的宽.设该长方形草坪的宽为x m,下面所列方程正确的是( )
A.x+10=132 B.2x+10=132
C.2(2x+10)=132 D.2(x-10)=132
7.一个长方形的周长是40 cm,若将长减少8 cm,宽增加2 cm,长方形就变成了正方形,则正方形的边长为( )
A.6 cm B.7 cm C.8 cm D.9 cm
8.用长12 cm的铁丝围成一个长是宽的2倍的长方形,则该长方形的面积是 .
9.小明家打算靠墙(墙长14 m)修建一个长方形养鸡场(靠墙的一边作为长),另三边用35 m长的竹篱笆围成,小明的爸爸打算让养鸡场的长比宽多2 m,小明的妈妈打算让养鸡场的长比宽多5 m,你认为他们谁的设计合理 按照这种设计,养鸡场的面积是多少平方米
10.现有大、小两种纸杯与甲、乙两桶果汁,其中小纸杯与大纸杯的容量之比为2∶3,甲桶果汁与乙桶果汁的体积之比为4∶5.若甲桶内的果汁刚好装满小纸杯120个,则乙桶内的果汁最多可装满大纸杯的个数为( )
A.64 B.100 C.144 D.225
11.在长方形ABCD中放入六个相同的小长方形,尺寸如图示,求小长方形的宽AE.若设AE=x cm,则依题意可得方程( )
A.6+2x=14-3x B.6+2x=x+(14-3x)
C.14-2x=6 D.6+2x=14-x
12.有A,B两个圆柱形容器,A容器的底面积是B容器的底面积的2倍,A容器内的水高为10 cm,B容器是空的,B容器的内壁高度为21 cm.若把A容器内的水全部倒入B容器中,则水会不会溢出
13.用一根线绳可围成边长为7 cm的正方形.若用此线绳改围成长比宽大2 cm的长方形,则长方形的面积是多少
14.由六个正方形拼成的一个长方形.已知最小的正方形的面积为1,则此长方形的面积是 .
15.实验室里,水平桌面上有甲、乙、丙三个相同高度的圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的10 cm高处连通(即管子底部离容器底10 cm),现三个容器中只有乙中有水,水位为4 cm,如图示.若每分钟同时向甲和丙注入相同量的水,开始注水1 min后,甲的水位上升3 cm,则开始注水多长时间后,甲的水位比乙高1 cm
答案
1.D 2.B
3.C 设应截取的圆钢长为x mm.根据题意,得2πx=2π×18,
解得x=450.
4.解:设应截取x mm长的圆钢.由题意,得
π2x=300×300×90,解得x=.
因此,应截取 mm长的圆钢.
5.解:设容器内水面将升高x m.
根据题意,得0.32π×0.5=0.52π·x,
解得x=0.18.
因此,容器内水面将升高0.18 m.
6.C 因为长方形草坪的长比宽多10 m,宽为x m,
所以长为(x+10)m.
因为它的周长是132 m,
所以2×(x+10+x)=132.
整理,得2(2x+10)=132.
故选C.
7.B 设正方形的边长为x cm,则长方形的长、宽分别为(x+8)cm,(x-2)cm.依题意,得2(x+8+x-2)=40,解得x=7.
即正方形的边长为7 cm.
8.8cm2 设围成的长方形的宽为x cm,则长为2x cm.根据题意,得2(x+2x)=12,解得x=2.所以2x=4.所以围成的长方形的面积为2×4=8(cm2).
9. 本题“墙长14 m”是一个限制条件,即所建的养鸡场的长不能大于14 m,同时我们还要计算面积的大小.
解:设养鸡场的宽为x m.
①按小明爸爸的设计,其长应为(x+2)m .依题意,得x+2+2x=35,解得x=11,11+2=13(m)<墙长14 m,所以小明爸爸的设计合理,这时养鸡场的面积为13×11=143(m2);
②按小明妈妈的设计,其长应为(x+5)m .依题意,得x+5+2x=35,解得x=10,10+5=15(m)>墙长14 m,所以小明妈妈的设计不符合实际.
因此小明爸爸的设计合理,按照这种设计养鸡场的面积为143 m2.
10.B 设乙桶内的果汁最多可装满x个大纸杯,小纸杯的容量为2a,则大纸杯的容量为3a.
根据题意,得(120×2a)∶3ax =4∶5,解得 x=100.
11.B
12.解:设B容器的底面积为S,A容器内的水全部倒入B容器后水的高度为x cm.
根据题意,得2×S×10=S×x,解得x=20.因为20<21,即B容器内水的高度小于B容器的内壁高度,所以水不会溢出.
13. 求长方形的面积,应先求出长方形的长和宽,有两个量需求,可先设长为x cm,由长=宽+2 cm,得宽为(x-2)cm,再由“变化前的周长=变化后的周长”这个等量关系列出方程.
解:设长方形的长为x cm,则宽为(x-2)cm,则4×7=2[x+(x-2)],解得x=8,8-2=6(cm),
所以该长方形的面积是8×6=48(cm2).
14.143 因为最小的正方形面积为1,所以其边长为1.设最大的正方形的边长为x,那么其他正方形按从大到小的顺序,边长依次是x-1,x-2,x-3,x-3,根据长方形的长是相等的,可得
x+(x-1)=(x-2)+2(x-3),解得x=7,所以长方形的面积为(7+6)×(6+5)=143.
15.解:分两种情况讨论:①当甲中的水未流入乙中时,因为乙中的水位为4 cm,甲的水位比乙高1 cm,所以甲的水位为5 cm.因为注水1 min,甲的水位上升3 cm,所以开始注入5÷3=(min)水量后,甲的水位比乙高1 cm;②当甲中的水流入乙中时,因为甲的水位比乙高1 cm,所以此时甲、丙中的水位为10 cm,则乙中的水位为9 cm.因为甲、乙、丙底面半径之比为1∶2∶1,所以设甲、丙的底面半径为r,则乙的底面半径为2r.所以开始所需时间为=(min).
综上,注水 min或 min后,甲的水位比乙高1 cm.
知识点 1 等积变形问题
1.已知底面半径为5 cm、高为7 cm的圆柱体的体积是底面直径为4 cm、高为x cm的圆柱体的体积的5倍,则下列方程正确的是( )
A.5π×42x=π×102×7
B.π×42x=5π×102×7
C.5π×2x=π×2×7
D.5π×2x=π×52×7
2.[2020·青海] 如图根据图中的信息,可得正确的方程是( )
A.π×x=π××(x-5)
B.π×x=π××(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
3.要锻造一个直径为200 mm、厚度为18 mm的钢圆盘,现有直径为40 mm的圆钢,不计损耗,则应截取的圆钢长为( )
A.350 mm B.400 mm
C.450 mm D.500 mm
4.如图用直径为200 mm的圆钢锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯底板,应截取多长的圆钢
5.如图一圆柱形容器的底面半径为0.5 m,高为1.5 m,里面盛有1 m深的水,将底面半径为0.3 m、高为0.5 m的圆柱形铁块沉入水中,则容器内水面将升高多少米
知识点 2 根据周长、面积列方程
6.一块长方形草坪的长比宽多10 m,它的周长是132 m,求该长方形草坪的宽.设该长方形草坪的宽为x m,下面所列方程正确的是( )
A.x+10=132 B.2x+10=132
C.2(2x+10)=132 D.2(x-10)=132
7.一个长方形的周长是40 cm,若将长减少8 cm,宽增加2 cm,长方形就变成了正方形,则正方形的边长为( )
A.6 cm B.7 cm C.8 cm D.9 cm
8.用长12 cm的铁丝围成一个长是宽的2倍的长方形,则该长方形的面积是 .
9.小明家打算靠墙(墙长14 m)修建一个长方形养鸡场(靠墙的一边作为长),另三边用35 m长的竹篱笆围成,小明的爸爸打算让养鸡场的长比宽多2 m,小明的妈妈打算让养鸡场的长比宽多5 m,你认为他们谁的设计合理 按照这种设计,养鸡场的面积是多少平方米
10.现有大、小两种纸杯与甲、乙两桶果汁,其中小纸杯与大纸杯的容量之比为2∶3,甲桶果汁与乙桶果汁的体积之比为4∶5.若甲桶内的果汁刚好装满小纸杯120个,则乙桶内的果汁最多可装满大纸杯的个数为( )
A.64 B.100 C.144 D.225
11.在长方形ABCD中放入六个相同的小长方形,尺寸如图示,求小长方形的宽AE.若设AE=x cm,则依题意可得方程( )
A.6+2x=14-3x B.6+2x=x+(14-3x)
C.14-2x=6 D.6+2x=14-x
12.有A,B两个圆柱形容器,A容器的底面积是B容器的底面积的2倍,A容器内的水高为10 cm,B容器是空的,B容器的内壁高度为21 cm.若把A容器内的水全部倒入B容器中,则水会不会溢出
13.用一根线绳可围成边长为7 cm的正方形.若用此线绳改围成长比宽大2 cm的长方形,则长方形的面积是多少
14.由六个正方形拼成的一个长方形.已知最小的正方形的面积为1,则此长方形的面积是 .
15.实验室里,水平桌面上有甲、乙、丙三个相同高度的圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的10 cm高处连通(即管子底部离容器底10 cm),现三个容器中只有乙中有水,水位为4 cm,如图示.若每分钟同时向甲和丙注入相同量的水,开始注水1 min后,甲的水位上升3 cm,则开始注水多长时间后,甲的水位比乙高1 cm
答案
1.D 2.B
3.C 设应截取的圆钢长为x mm.根据题意,得2πx=2π×18,
解得x=450.
4.解:设应截取x mm长的圆钢.由题意,得
π2x=300×300×90,解得x=.
因此,应截取 mm长的圆钢.
5.解:设容器内水面将升高x m.
根据题意,得0.32π×0.5=0.52π·x,
解得x=0.18.
因此,容器内水面将升高0.18 m.
6.C 因为长方形草坪的长比宽多10 m,宽为x m,
所以长为(x+10)m.
因为它的周长是132 m,
所以2×(x+10+x)=132.
整理,得2(2x+10)=132.
故选C.
7.B 设正方形的边长为x cm,则长方形的长、宽分别为(x+8)cm,(x-2)cm.依题意,得2(x+8+x-2)=40,解得x=7.
即正方形的边长为7 cm.
8.8cm2 设围成的长方形的宽为x cm,则长为2x cm.根据题意,得2(x+2x)=12,解得x=2.所以2x=4.所以围成的长方形的面积为2×4=8(cm2).
9. 本题“墙长14 m”是一个限制条件,即所建的养鸡场的长不能大于14 m,同时我们还要计算面积的大小.
解:设养鸡场的宽为x m.
①按小明爸爸的设计,其长应为(x+2)m .依题意,得x+2+2x=35,解得x=11,11+2=13(m)<墙长14 m,所以小明爸爸的设计合理,这时养鸡场的面积为13×11=143(m2);
②按小明妈妈的设计,其长应为(x+5)m .依题意,得x+5+2x=35,解得x=10,10+5=15(m)>墙长14 m,所以小明妈妈的设计不符合实际.
因此小明爸爸的设计合理,按照这种设计养鸡场的面积为143 m2.
10.B 设乙桶内的果汁最多可装满x个大纸杯,小纸杯的容量为2a,则大纸杯的容量为3a.
根据题意,得(120×2a)∶3ax =4∶5,解得 x=100.
11.B
12.解:设B容器的底面积为S,A容器内的水全部倒入B容器后水的高度为x cm.
根据题意,得2×S×10=S×x,解得x=20.因为20<21,即B容器内水的高度小于B容器的内壁高度,所以水不会溢出.
13. 求长方形的面积,应先求出长方形的长和宽,有两个量需求,可先设长为x cm,由长=宽+2 cm,得宽为(x-2)cm,再由“变化前的周长=变化后的周长”这个等量关系列出方程.
解:设长方形的长为x cm,则宽为(x-2)cm,则4×7=2[x+(x-2)],解得x=8,8-2=6(cm),
所以该长方形的面积是8×6=48(cm2).
14.143 因为最小的正方形面积为1,所以其边长为1.设最大的正方形的边长为x,那么其他正方形按从大到小的顺序,边长依次是x-1,x-2,x-3,x-3,根据长方形的长是相等的,可得
x+(x-1)=(x-2)+2(x-3),解得x=7,所以长方形的面积为(7+6)×(6+5)=143.
15.解:分两种情况讨论:①当甲中的水未流入乙中时,因为乙中的水位为4 cm,甲的水位比乙高1 cm,所以甲的水位为5 cm.因为注水1 min,甲的水位上升3 cm,所以开始注入5÷3=(min)水量后,甲的水位比乙高1 cm;②当甲中的水流入乙中时,因为甲的水位比乙高1 cm,所以此时甲、丙中的水位为10 cm,则乙中的水位为9 cm.因为甲、乙、丙底面半径之比为1∶2∶1,所以设甲、丙的底面半径为r,则乙的底面半径为2r.所以开始所需时间为=(min).
综上,注水 min或 min后,甲的水位比乙高1 cm.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
