19.1.1平行四边形性质(1)学案
文档属性
| 名称 | 19.1.1平行四边形性质(1)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 127.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-24 00:00:00 | ||
图片预览

文档简介
学科:数学 年级:八年级 主备人: 审核人: 课题:平行四边形性质1 课型:预习+展示 小主人姓名:
*学习目标*:1、掌握平行四边形的概念和平行四边形对边、对角相等的性质. 2、会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.*学习重点*:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.*学习难点*:运用平行四边形的性质进行有关的论证和计算.
学习过程 学法指导
一。*知识回顾*1.有两组对边__________________的四边形叫平形四边形,平行四边形用“______”表示,平行四边形ABCD记作__________。2.如图□ABCD中,对边有______组,分别是___________________,对角有_____组,分别是_________________,对角线有______条,它们是__________________。二.*能力生成*活动一 平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?根据定义画一个平行四边形,观察它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致? (1)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.
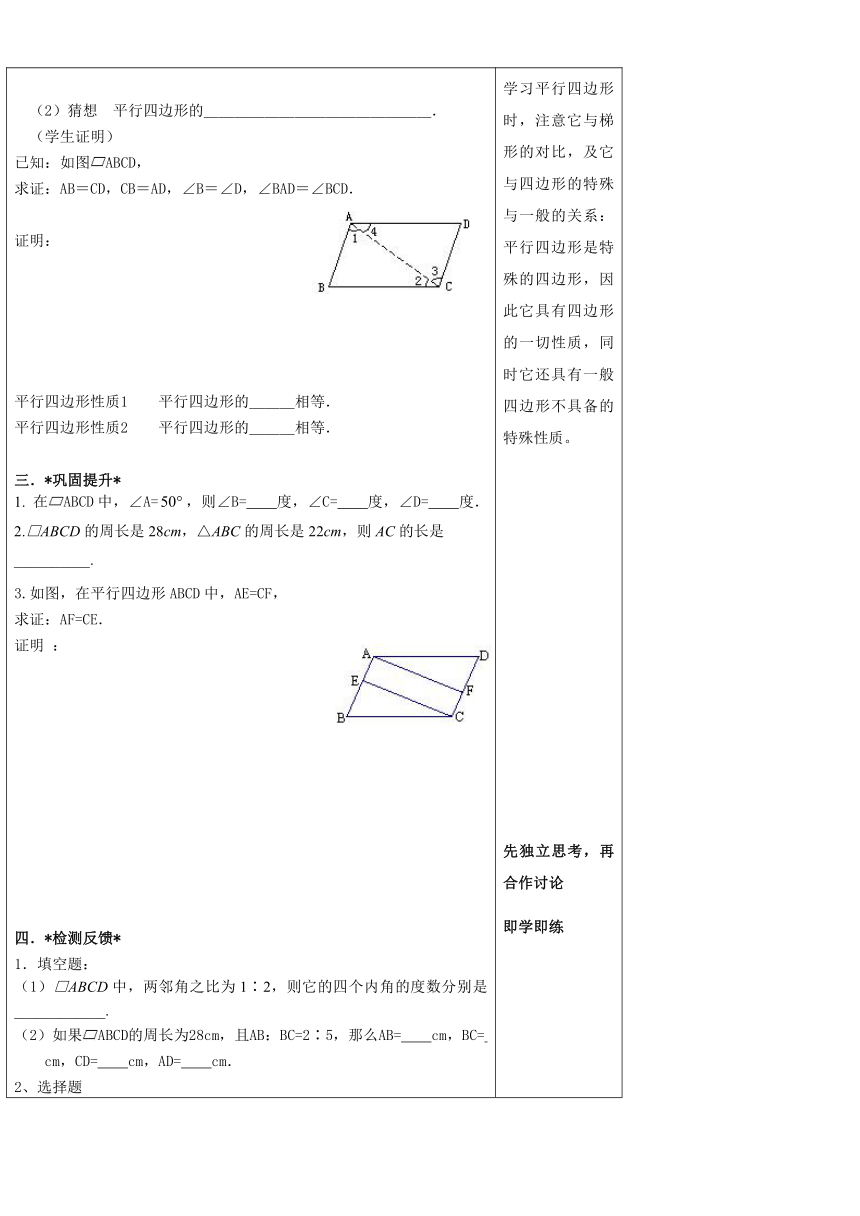
(2)猜想 平行四边形的_______________.(学生证明)已知:如图ABCD,求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD. 证明: 平行四边形性质1 平行四边形的___相等.平行四边形性质2 平行四边形的___相等.三.*巩固提升*1. 在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.3.如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.证明 : 四.*检测反馈*1.填空题: (1)□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.(2)如果ABCD的周长为28cm,且AB:BC=2∶5,那么AB= cm,BC= cm,CD= cm,AD= cm.2、选择题①.在下列图形的性质中,平行四边形不一定具有的是( ).(A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是②.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( ).(A)4个 (B)5个 (C)8个 (D)9个2.证明题如图,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.3、证明题:如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.五.*课堂小结*本节课我们所学的知识有:1.平行四边形性质12.平行四边形性质2 学习平行四边形时,注意它与梯形的对比,及它与四边形的特殊与一般的关系:平行四边形是特殊的四边形,因此它具有四边形的一切性质,同时它还具有一般四边形不具备的特殊性质。先独立思考,再合作讨论即学即练注意内角和公式的应用从平行四边形的主要元素-----边、角、对角线的位置关系及数量关系入手一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
*学习目标*:1、掌握平行四边形的概念和平行四边形对边、对角相等的性质. 2、会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.*学习重点*:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.*学习难点*:运用平行四边形的性质进行有关的论证和计算.
学习过程 学法指导
一。*知识回顾*1.有两组对边__________________的四边形叫平形四边形,平行四边形用“______”表示,平行四边形ABCD记作__________。2.如图□ABCD中,对边有______组,分别是___________________,对角有_____组,分别是_________________,对角线有______条,它们是__________________。二.*能力生成*活动一 平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?根据定义画一个平行四边形,观察它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致? (1)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.
(2)猜想 平行四边形的_______________.(学生证明)已知:如图ABCD,求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD. 证明: 平行四边形性质1 平行四边形的___相等.平行四边形性质2 平行四边形的___相等.三.*巩固提升*1. 在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.3.如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.证明 : 四.*检测反馈*1.填空题: (1)□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.(2)如果ABCD的周长为28cm,且AB:BC=2∶5,那么AB= cm,BC= cm,CD= cm,AD= cm.2、选择题①.在下列图形的性质中,平行四边形不一定具有的是( ).(A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是②.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( ).(A)4个 (B)5个 (C)8个 (D)9个2.证明题如图,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.3、证明题:如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.五.*课堂小结*本节课我们所学的知识有:1.平行四边形性质12.平行四边形性质2 学习平行四边形时,注意它与梯形的对比,及它与四边形的特殊与一般的关系:平行四边形是特殊的四边形,因此它具有四边形的一切性质,同时它还具有一般四边形不具备的特殊性质。先独立思考,再合作讨论即学即练注意内角和公式的应用从平行四边形的主要元素-----边、角、对角线的位置关系及数量关系入手一分耕耘一分收获,你的收获有多大!
注意双色笔的使用哦!
