人教A版(2019)选择性必修第三册-7.1.2全概率公式 课件(共13张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册-7.1.2全概率公式 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
7.1条件概率和全概率公式
7.1.2全概率公式
学习目标(1min)
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
问题导学(5min)
阅读课本P49-52
思考:从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球
不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红
球的概率是多大?如何计算这个概率呢
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
解析:
点拨精讲(25min)
思考:从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球
不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红
球的概率是多大?如何计算这个概率呢
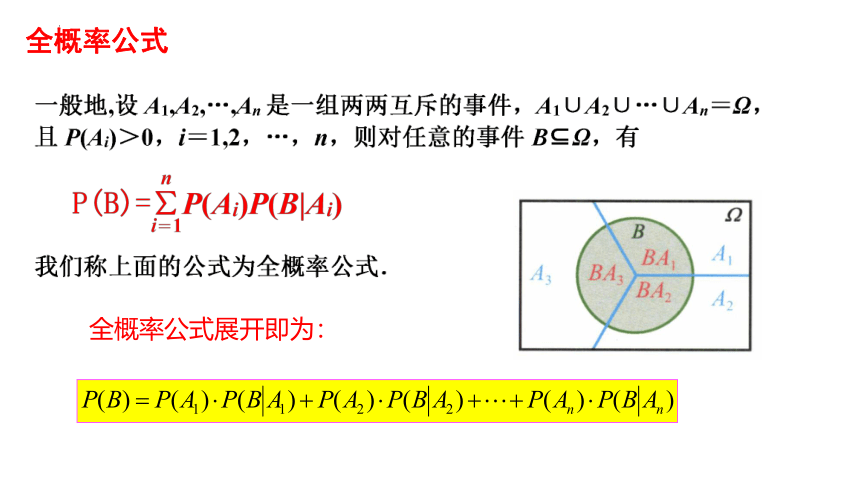
全概率公式
全概率公式展开即为:
例1. 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
解:设A1=“第1天去A餐厅用餐”, B1=“第1天去B餐厅用餐”,
A2=“第2天去A餐厅用餐”,则Ω=,根据题意得
P(A1)=P(B1)=0.5, P(A2|A1)=0.6, P(A2|B1)=0.8,
由全概率公式,得
P(A2)= P(A1) P(A2|A1)+ P(B1) P(A2|B1)=0.5×0.6+0.5×0.8=0.7
因此,王同学第2天去A餐厅用餐得概率为0.7.
归纳总结
例2:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
解:B=“任取一个零件为次品”,
Ai=“零件为第i台车床加工”(i=1,2,3),
则,且互斥,根据题意得
P(A1)=0.25, P(A2)=0.3, P(A3)=0.45,
P(B|A1)=0.06, P(B|A2)= P(B|A3)=0.05.
(1)由全概率公式,得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+ P(A3)P(B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05=0.0525
(2)“如果取到得零件是次品,计算它是第i(i =1,2,3)台车床加工的概率”,
就是计算在B发生的条件下,事件Ai发生的概率.
同理可得;
*贝叶斯公式:
1.全概率公式
2*.贝叶斯公式
课堂小结(1min)
当堂检测(13min)
1.市场上有甲、乙、丙三家工厂生产的同一品牌产品,已知三家工厂的市场占有率分别为30%,20%,50%,且三家工厂的次品率分别为3%,3%,1%,试求市场上该品牌产品的次品率.
解 设A表示买到一件次品;B1,B2,B3分别表示买到一件甲厂、乙厂、丙厂的产品.则
P(A)=P(AB1)+P(AB2)+P(AB3)=P(B1)P(A|B1)+P(B2)·P(A|B2)+P(B3)P(A|B3)=30%×3%+20%×3%+50%×1%=2%.
2.对以往的数据分析结果表明,当机器调整良好时,产品的合格率为90%,而当机器发生某一故障时,其合格率为30%.每天早上机器开动时,机器调整良好的概率为75%.已知某天早上第一件产品是合格品,则机器调整良好的概率是多少?
2.对以往的数据分析结果表明,当机器调整良好时,产品的合格率为90%,而当机器发生某一故障时,其合格率为30%.每天早上机器开动时,机器调整良好的概率为75%.已知某天早上第一件产品是合格品,则机器调整良好的概率是多少?
7.1条件概率和全概率公式
7.1.2全概率公式
学习目标(1min)
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
问题导学(5min)
阅读课本P49-52
思考:从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球
不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红
球的概率是多大?如何计算这个概率呢
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
解析:
点拨精讲(25min)
思考:从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的球
不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红
球的概率是多大?如何计算这个概率呢
全概率公式
全概率公式展开即为:
例1. 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
解:设A1=“第1天去A餐厅用餐”, B1=“第1天去B餐厅用餐”,
A2=“第2天去A餐厅用餐”,则Ω=,根据题意得
P(A1)=P(B1)=0.5, P(A2|A1)=0.6, P(A2|B1)=0.8,
由全概率公式,得
P(A2)= P(A1) P(A2|A1)+ P(B1) P(A2|B1)=0.5×0.6+0.5×0.8=0.7
因此,王同学第2天去A餐厅用餐得概率为0.7.
归纳总结
例2:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
解:B=“任取一个零件为次品”,
Ai=“零件为第i台车床加工”(i=1,2,3),
则,且互斥,根据题意得
P(A1)=0.25, P(A2)=0.3, P(A3)=0.45,
P(B|A1)=0.06, P(B|A2)= P(B|A3)=0.05.
(1)由全概率公式,得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+ P(A3)P(B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05=0.0525
(2)“如果取到得零件是次品,计算它是第i(i =1,2,3)台车床加工的概率”,
就是计算在B发生的条件下,事件Ai发生的概率.
同理可得;
*贝叶斯公式:
1.全概率公式
2*.贝叶斯公式
课堂小结(1min)
当堂检测(13min)
1.市场上有甲、乙、丙三家工厂生产的同一品牌产品,已知三家工厂的市场占有率分别为30%,20%,50%,且三家工厂的次品率分别为3%,3%,1%,试求市场上该品牌产品的次品率.
解 设A表示买到一件次品;B1,B2,B3分别表示买到一件甲厂、乙厂、丙厂的产品.则
P(A)=P(AB1)+P(AB2)+P(AB3)=P(B1)P(A|B1)+P(B2)·P(A|B2)+P(B3)P(A|B3)=30%×3%+20%×3%+50%×1%=2%.
2.对以往的数据分析结果表明,当机器调整良好时,产品的合格率为90%,而当机器发生某一故障时,其合格率为30%.每天早上机器开动时,机器调整良好的概率为75%.已知某天早上第一件产品是合格品,则机器调整良好的概率是多少?
2.对以往的数据分析结果表明,当机器调整良好时,产品的合格率为90%,而当机器发生某一故障时,其合格率为30%.每天早上机器开动时,机器调整良好的概率为75%.已知某天早上第一件产品是合格品,则机器调整良好的概率是多少?
