人教版八年级下册16.2二次根式的乘除(第二课时)课件(共16张PPT)
文档属性
| 名称 | 人教版八年级下册16.2二次根式的乘除(第二课时)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 477.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 06:37:11 | ||
图片预览






文档简介
(共16张PPT)
二次根式的乘除(2)
授课人:
班级:
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
想一想:上一节课我们学习了什么呢?
温故旧知
二次根式的乘法法则
()
两个因数(或两个因式)的算式平方根的积,等于这两个因数(或两个因式)积的算式平方根。
二次根式的乘法法则的逆应用
()
语言描述:
这两个因数(或两个因式)积的算式平方根,等于两个因数(或两个因式)的算式平方根的积
语言描述:
想一想:二次根式的除法有没有类似的法则呢
?
除法是乘法的逆运算
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
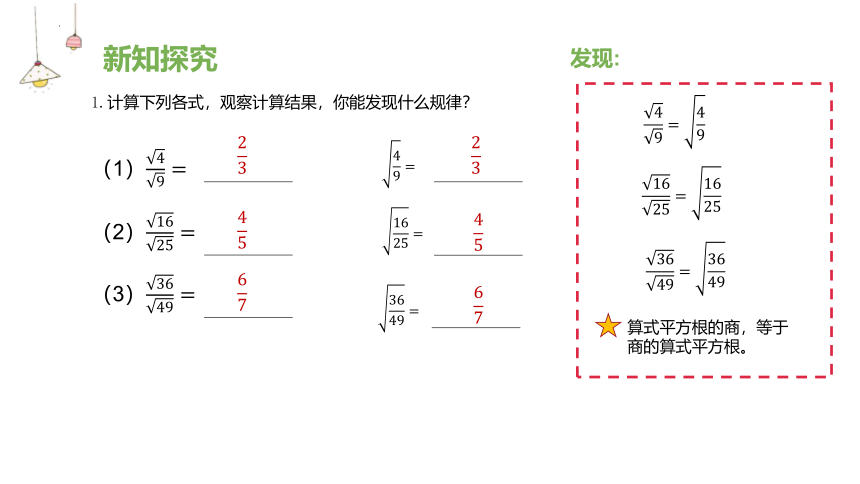
1.计算下列各式,观察计算结果,你能发现什么规律?
新知探究
发现:
(1)
(2)
(3)
算式平方根的商,等于商的算式平方根。
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
新知探究
()
二次根式的乘法法则
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
二次根式的除法法则
新知探究
()
用语言描述:
两个因数(或两个因式)的算式平方根的商,等于这两个因数(或两个因式)商的算式平方根。
例1 计算:
小试牛刀
二次根式除法法则:
, ()
(1)
(2)
解:(1)
或
(2)
同学们想一想,能否将二次根式 进行化简?
逆向思考
二次根式除法法则:
, ()
解:
, ()
二次根式除法法则的逆应用
例2 计算:
小试牛刀
(1)
(2)
解:(1)
(2)
例3 计算:
小试牛刀
(1)
(2)
解:(1)
(2)
(2)
(3)
再探究
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它
是最简了?
问题 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们已经是最简二次根式了吗?
再探究
可以发现这些式子有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
巩固新知
问题3 辨别下列二次根式是否是最简二次根式.
(1) (2) (3) (4)
.
巩固新知
问题4 把下列二次根式化成最简二次根式.
(1) (2) (3) (4)
解:(1)
(2)
(3)
(4)
1.二次根式的除法法则:
(1).被开方数不含分母;
(2).被开方数不含能开得尽方的因数或因式.
2.最简二次根式:
可以用二次根式的性质,乘除运算法则及分数基本性质化去分母中的根号.
课堂小结
()
如何化去分母中的根号?
谢谢观看
Thank you for watching
二次根式的乘除(2)
授课人:
班级:
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
想一想:上一节课我们学习了什么呢?
温故旧知
二次根式的乘法法则
()
两个因数(或两个因式)的算式平方根的积,等于这两个因数(或两个因式)积的算式平方根。
二次根式的乘法法则的逆应用
()
语言描述:
这两个因数(或两个因式)积的算式平方根,等于两个因数(或两个因式)的算式平方根的积
语言描述:
想一想:二次根式的除法有没有类似的法则呢
?
除法是乘法的逆运算
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
1.计算下列各式,观察计算结果,你能发现什么规律?
新知探究
发现:
(1)
(2)
(3)
算式平方根的商,等于商的算式平方根。
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
新知探究
()
二次根式的乘法法则
(前四个纹理为矢量素材,可直接通过更改形状填充更改颜色)
二次根式的除法法则
新知探究
()
用语言描述:
两个因数(或两个因式)的算式平方根的商,等于这两个因数(或两个因式)商的算式平方根。
例1 计算:
小试牛刀
二次根式除法法则:
, ()
(1)
(2)
解:(1)
或
(2)
同学们想一想,能否将二次根式 进行化简?
逆向思考
二次根式除法法则:
, ()
解:
, ()
二次根式除法法则的逆应用
例2 计算:
小试牛刀
(1)
(2)
解:(1)
(2)
例3 计算:
小试牛刀
(1)
(2)
解:(1)
(2)
(2)
(3)
再探究
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它
是最简了?
问题 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们已经是最简二次根式了吗?
再探究
可以发现这些式子有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
巩固新知
问题3 辨别下列二次根式是否是最简二次根式.
(1) (2) (3) (4)
.
巩固新知
问题4 把下列二次根式化成最简二次根式.
(1) (2) (3) (4)
解:(1)
(2)
(3)
(4)
1.二次根式的除法法则:
(1).被开方数不含分母;
(2).被开方数不含能开得尽方的因数或因式.
2.最简二次根式:
可以用二次根式的性质,乘除运算法则及分数基本性质化去分母中的根号.
课堂小结
()
如何化去分母中的根号?
谢谢观看
Thank you for watching
