北师大版数学八年级上册同步课时练习:第4章 一次函数 4 第2课时 借助单个一次函数图象解决有关问题 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级上册同步课时练习:第4章 一次函数 4 第2课时 借助单个一次函数图象解决有关问题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 10:24:20 | ||
图片预览


文档简介
第2课时 借助单个一次函数图象解决有关问题
知识点 1 单个一次函数图象的应用
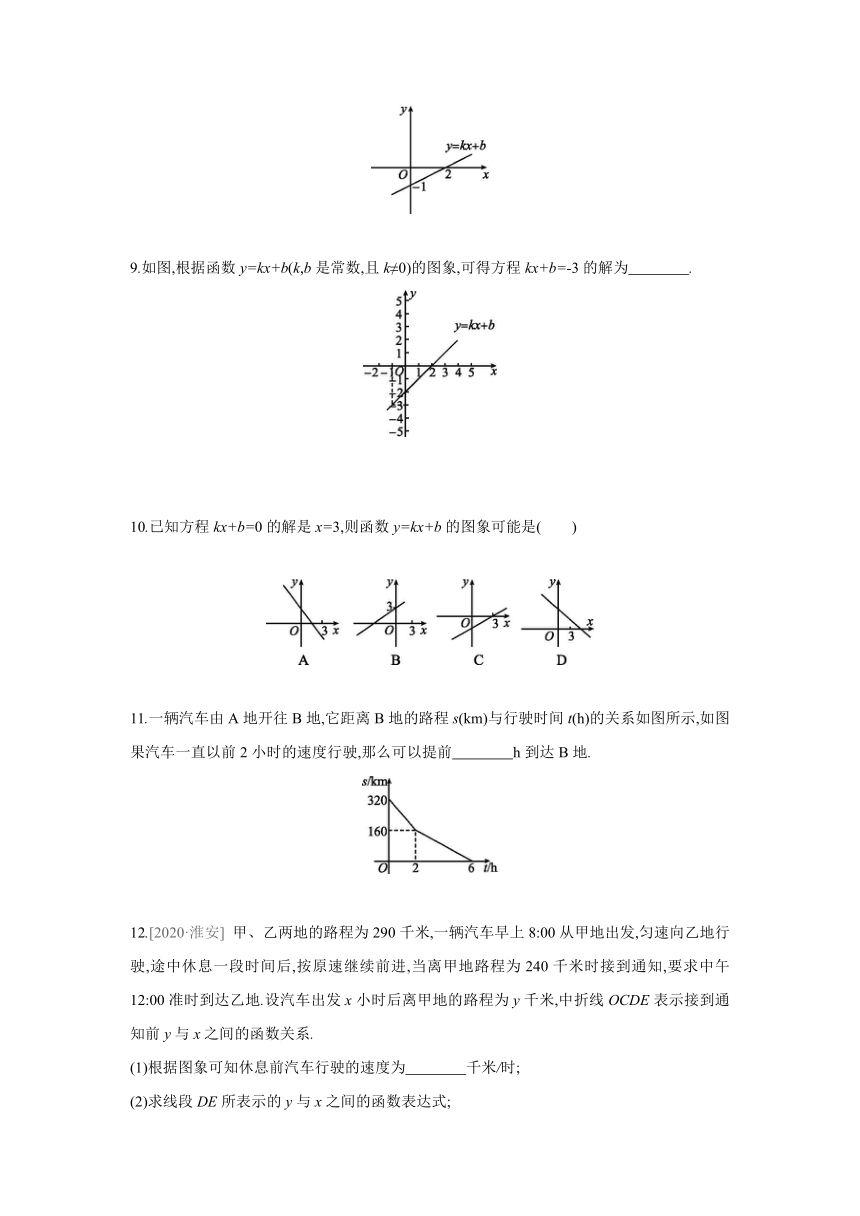
1.一根蜡烛长30 cm,点燃后每小时燃烧5 cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(h)之间的函数关系用图象可以表示为( )
2.示的是某植物生长t天后的高度y(单位: cm)与t之间的关系,根据图象,下列结论不正确的是( )
A.该植物初始的高度是3 cm
B.该植物生长10天后的高度是10 cm
C.该植物平均每天生长0.7 cm
D.y与t之间的函数关系式是y=t+3
3.示是一辆汽车油箱里的剩油量y(L)与行驶时间x(h)的函数图象,则汽车行驶前油箱里有 L汽油,经过 h耗尽汽油,平均每小时耗油 L,油箱中剩油量y(L)与行驶时间x(h)之间的函数关系式是 ,自变量x的取值范围是 .
4.国内航空规定,乘坐飞机经济舱的旅客所携带行李超过可免费携带行李的最大质量后,行李的质量x(kg)与其运费y(元)之间是一次函数关系,其图象如图示,那么旅客可免费携带的行李的最大质量为 .
5.有一种节能型轿车的储气箱最多可装天然气50 L,加满天然气后,储气箱中的剩余天然气量y(L)与轿车行驶路程x(km)之间的关系如图所示,根据图象回答下列问题:
(1)一箱天然气可供轿车行驶多少千米
(2)轿车每行驶200 km消耗天然气多少升
(3)写出y与x之间的函数表达式.
6.某生物小组观察一植物的生长过程,得到植物的高度y(厘米)与观察时间x(天)的关系,并画出如图所示的图象(AC是线段,射线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高
(2)求AC段对应的函数表达式,并求该植物最高长到了多少厘米.
知识点 2 一次函数与一元一次方程
7.一次函数y=kx+b的图象如图所示,那么方程kx+b=0的解是( )
A.x=-1 B.x=2
C.x= D.x=0
8.已知关于x的方程ax+b=0的解是x=-5,则函数y=ax+b与x轴的交点坐标是 .
9.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,可得方程kx+b=-3的解为 .
10.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
11.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如图果汽车一直以前2小时的速度行驶,那么可以提前 h到达B地.
12.[2020·淮安] 甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为y千米,中折线OCDE表示接到通知前y与x之间的函数关系.
(1)根据图象可知休息前汽车行驶的速度为 千米/时;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达乙地 请说明理由.
13.张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①,然后,他用这8块瓷砖又拼出一个大正方形,如图图②,中间恰好空出一个边长为1的小正方形(阴影部分),假设小长方形瓷砖的长为y,宽为x.
(1)求出图①中y与x之间的函数表达式(不需要写出自变量x的取值范围);
(2)求出图②中y与x之间的函数表达式(不需要写出自变量x的取值范围);
(3)在图③中作出(1)(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义.
答案
1.B 2.D
3.40 8 5 y=-5x+40 0≤x≤8
4.20 kg 设y与x之间的函数关系式为y=kx+b,观察图象可知,旅客携带的行李质量超过可免费携带的行李的最大质量后,行李质量每增加1 kg,运费增加30元,因此k=30,y=30x+b.将点(30,300)的坐标代入y=30x+b,得b=-600,所以旅客携带的行李质量超过可免费携带的行李的最大质量后,运费y与行李质量x之间的关系式为y=30x-600.令y=0,得x=20,所以旅客可免费携带的行李的最大质量为20 kg.
5.解:(1)一箱天然气可供轿车行驶1000 km.
(2)200×(50÷1000)=10(L).
因此,轿车每行驶200 km消耗天然气10 L.
(3)设y与x之间的函数表达式为y=kx+b,把(0,50),(1000,0)代入,得b=50,1000k+b=0,解得k=-0.05,
故y与x之间的函数表达式为y=-0.05x+50(0≤x≤1000).
6. (1)根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高;
(2)设AC段对应的函数表达式为y=kx+b,然后根据点A,B的坐标求出AC段对应的函数表达式,再把x=50代入进行计算即可得解.
解:(1)因为CD∥x轴,
所以从第50天开始植物的高度不变.
故该植物从观察时起,50天以后停止长高.
(2)设AC段对应的函数表达式为y=kx+b.
因为函数图象经过点A(0,6),B(30,12),
所以b=6,30k+b=12,
解得k=.所以AC段对应的函数表达式为y=x+6(0≤x≤50).
当x=50时,y=×50+6=16.
所以该植物最高长到了16厘米.
7.B 8.(-5,0) 9.x=-1
10.C 由于方程kx+b=0的解是x=3,即x=3时,y=0,所以直线y=kx+b经过点(3,0),只有选项C符合题意.
11.2
12.解:(1)由图象可知,休息前汽车行驶的速度为80÷1=80(千米/时).故答案为80.
(2)设直线DE所表示的y与x之间的函数表达式为y=kx+b.
因为休息后按原速继续前进,所以k=80,所以y=80x+b.又因为直线DE经过点D(1.5,80),所以1.5×80+b=80,所以b=-40,
所以y=80x-40.当y=240时,x=3.5.故线段DE所表示的y与x之间的函数表达式为y=80x-40(1.5≤x≤3.5).
(3)不能.理由:接到通过后,汽车仍按原速行驶,则全程所需时间为290÷80+0.5=4.125(时),而8:00到12:00共有4小时.
因为4.125>4,所以接到通知后,汽车仍按原速行驶不能准时到达乙地.
13.解:(1)由图①,得3y=5x,得y=x.
(2)由图②,得2x-y=1,即y=2x-1.
(3)画出函数图象略.交点坐标为(3,5).
实际意义:小长方形瓷砖的长为5,宽为3时,即能围成图①所示的图形,又能围成图②所示的图形.
知识点 1 单个一次函数图象的应用
1.一根蜡烛长30 cm,点燃后每小时燃烧5 cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(h)之间的函数关系用图象可以表示为( )
2.示的是某植物生长t天后的高度y(单位: cm)与t之间的关系,根据图象,下列结论不正确的是( )
A.该植物初始的高度是3 cm
B.该植物生长10天后的高度是10 cm
C.该植物平均每天生长0.7 cm
D.y与t之间的函数关系式是y=t+3
3.示是一辆汽车油箱里的剩油量y(L)与行驶时间x(h)的函数图象,则汽车行驶前油箱里有 L汽油,经过 h耗尽汽油,平均每小时耗油 L,油箱中剩油量y(L)与行驶时间x(h)之间的函数关系式是 ,自变量x的取值范围是 .
4.国内航空规定,乘坐飞机经济舱的旅客所携带行李超过可免费携带行李的最大质量后,行李的质量x(kg)与其运费y(元)之间是一次函数关系,其图象如图示,那么旅客可免费携带的行李的最大质量为 .
5.有一种节能型轿车的储气箱最多可装天然气50 L,加满天然气后,储气箱中的剩余天然气量y(L)与轿车行驶路程x(km)之间的关系如图所示,根据图象回答下列问题:
(1)一箱天然气可供轿车行驶多少千米
(2)轿车每行驶200 km消耗天然气多少升
(3)写出y与x之间的函数表达式.
6.某生物小组观察一植物的生长过程,得到植物的高度y(厘米)与观察时间x(天)的关系,并画出如图所示的图象(AC是线段,射线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高
(2)求AC段对应的函数表达式,并求该植物最高长到了多少厘米.
知识点 2 一次函数与一元一次方程
7.一次函数y=kx+b的图象如图所示,那么方程kx+b=0的解是( )
A.x=-1 B.x=2
C.x= D.x=0
8.已知关于x的方程ax+b=0的解是x=-5,则函数y=ax+b与x轴的交点坐标是 .
9.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,可得方程kx+b=-3的解为 .
10.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
11.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如图果汽车一直以前2小时的速度行驶,那么可以提前 h到达B地.
12.[2020·淮安] 甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为y千米,中折线OCDE表示接到通知前y与x之间的函数关系.
(1)根据图象可知休息前汽车行驶的速度为 千米/时;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达乙地 请说明理由.
13.张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①,然后,他用这8块瓷砖又拼出一个大正方形,如图图②,中间恰好空出一个边长为1的小正方形(阴影部分),假设小长方形瓷砖的长为y,宽为x.
(1)求出图①中y与x之间的函数表达式(不需要写出自变量x的取值范围);
(2)求出图②中y与x之间的函数表达式(不需要写出自变量x的取值范围);
(3)在图③中作出(1)(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义.
答案
1.B 2.D
3.40 8 5 y=-5x+40 0≤x≤8
4.20 kg 设y与x之间的函数关系式为y=kx+b,观察图象可知,旅客携带的行李质量超过可免费携带的行李的最大质量后,行李质量每增加1 kg,运费增加30元,因此k=30,y=30x+b.将点(30,300)的坐标代入y=30x+b,得b=-600,所以旅客携带的行李质量超过可免费携带的行李的最大质量后,运费y与行李质量x之间的关系式为y=30x-600.令y=0,得x=20,所以旅客可免费携带的行李的最大质量为20 kg.
5.解:(1)一箱天然气可供轿车行驶1000 km.
(2)200×(50÷1000)=10(L).
因此,轿车每行驶200 km消耗天然气10 L.
(3)设y与x之间的函数表达式为y=kx+b,把(0,50),(1000,0)代入,得b=50,1000k+b=0,解得k=-0.05,
故y与x之间的函数表达式为y=-0.05x+50(0≤x≤1000).
6. (1)根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高;
(2)设AC段对应的函数表达式为y=kx+b,然后根据点A,B的坐标求出AC段对应的函数表达式,再把x=50代入进行计算即可得解.
解:(1)因为CD∥x轴,
所以从第50天开始植物的高度不变.
故该植物从观察时起,50天以后停止长高.
(2)设AC段对应的函数表达式为y=kx+b.
因为函数图象经过点A(0,6),B(30,12),
所以b=6,30k+b=12,
解得k=.所以AC段对应的函数表达式为y=x+6(0≤x≤50).
当x=50时,y=×50+6=16.
所以该植物最高长到了16厘米.
7.B 8.(-5,0) 9.x=-1
10.C 由于方程kx+b=0的解是x=3,即x=3时,y=0,所以直线y=kx+b经过点(3,0),只有选项C符合题意.
11.2
12.解:(1)由图象可知,休息前汽车行驶的速度为80÷1=80(千米/时).故答案为80.
(2)设直线DE所表示的y与x之间的函数表达式为y=kx+b.
因为休息后按原速继续前进,所以k=80,所以y=80x+b.又因为直线DE经过点D(1.5,80),所以1.5×80+b=80,所以b=-40,
所以y=80x-40.当y=240时,x=3.5.故线段DE所表示的y与x之间的函数表达式为y=80x-40(1.5≤x≤3.5).
(3)不能.理由:接到通过后,汽车仍按原速行驶,则全程所需时间为290÷80+0.5=4.125(时),而8:00到12:00共有4小时.
因为4.125>4,所以接到通知后,汽车仍按原速行驶不能准时到达乙地.
13.解:(1)由图①,得3y=5x,得y=x.
(2)由图②,得2x-y=1,即y=2x-1.
(3)画出函数图象略.交点坐标为(3,5).
实际意义:小长方形瓷砖的长为5,宽为3时,即能围成图①所示的图形,又能围成图②所示的图形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
