2013年九年级专题复习课 学一题解一类
文档属性
| 名称 | 2013年九年级专题复习课 学一题解一类 |

|
|
| 格式 | zip | ||
| 文件大小 | 341.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-24 00:00:00 | ||
图片预览




文档简介
课件20张PPT。关注学生学习 提高复习效率 学一题 解一类
------谈初中数学专题复习课
问题: 学生做题不能触类旁通,做过的题目稍作变化后就又不会做了,教师对每个大题都得一一讲解,而效果却不尽人意。主要原因:①对数学知识之间的联系缺乏认识;
②对题目考查的数学本质不清楚;
③做题只为做题,没有反思归纳;
解决问题
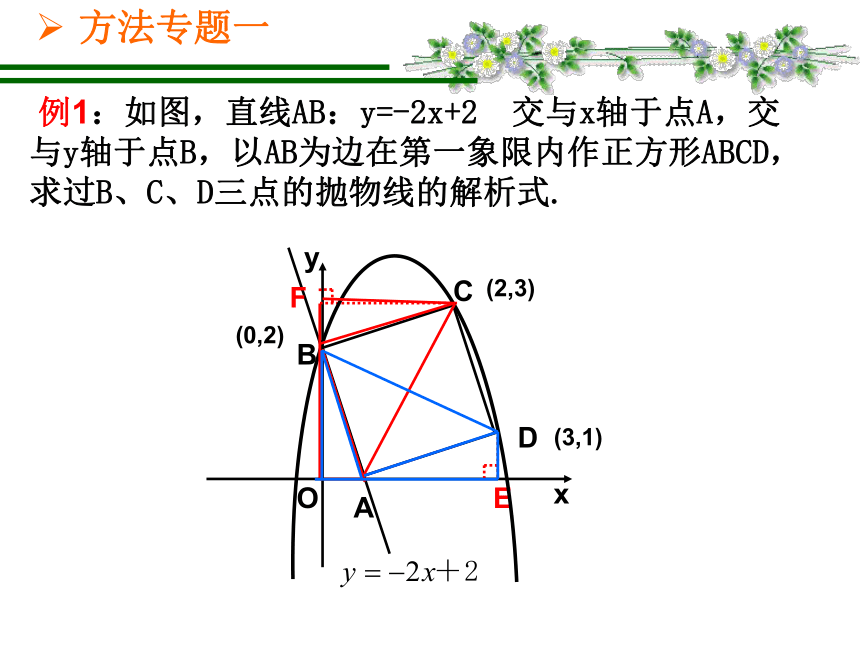
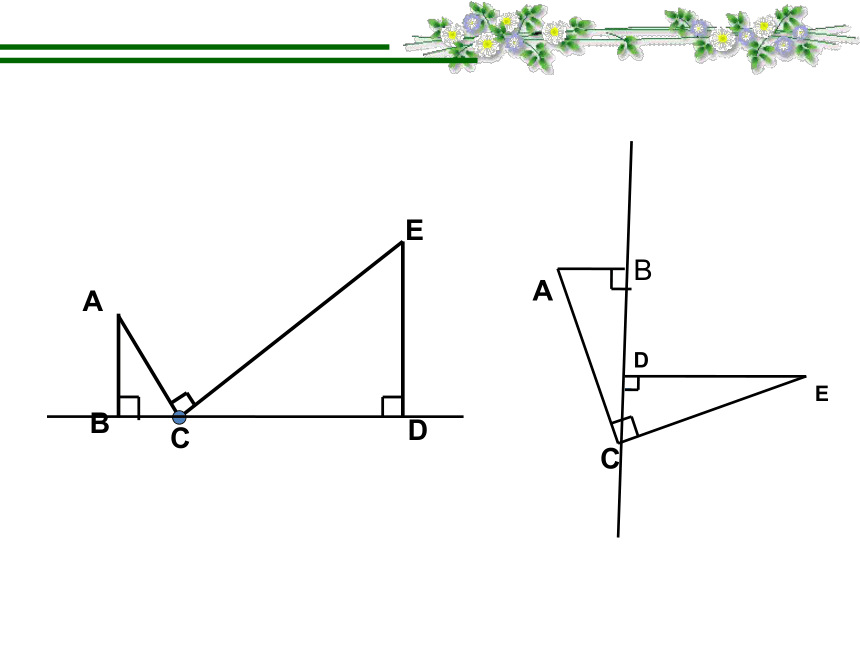
所以开展专题复习课,学一题解一类,安排有一定的系统性,针对性,串联性的解题训练,让散落的珍珠串成美丽的项链,既能帮助学生从题海中走出来,又可以有效提高总复习的效率。O(0,2)(2,3)(3,1) 例1:如图,直线AB:y=-2x+2 交与x轴于点A,交与y轴于点B,以AB为边在第一象限内作正方形ABCD,求过B、C、D三点的抛物线的解析式.方法专题一ACBEDACBED 1、 如图,直线 与y轴交于点A,与x轴交于点D,
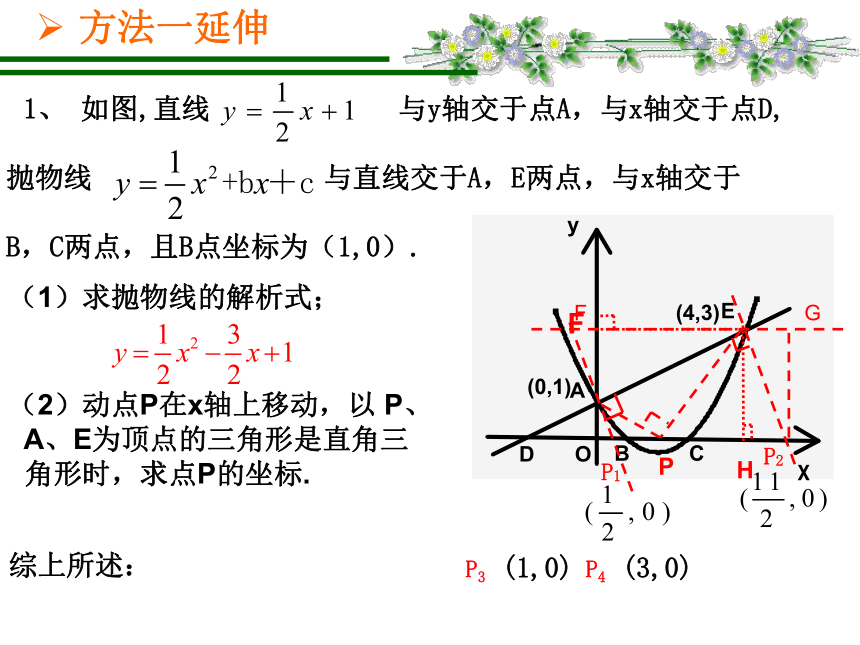
抛物线 与直线交于A,E两点,与x轴交于
B,C两点,且B点坐标为(1,0).
уχ(0,1)(1)求抛物线的解析式;(2)动点P在x轴上移动,以 P、
A、E为顶点的三角形是直角三
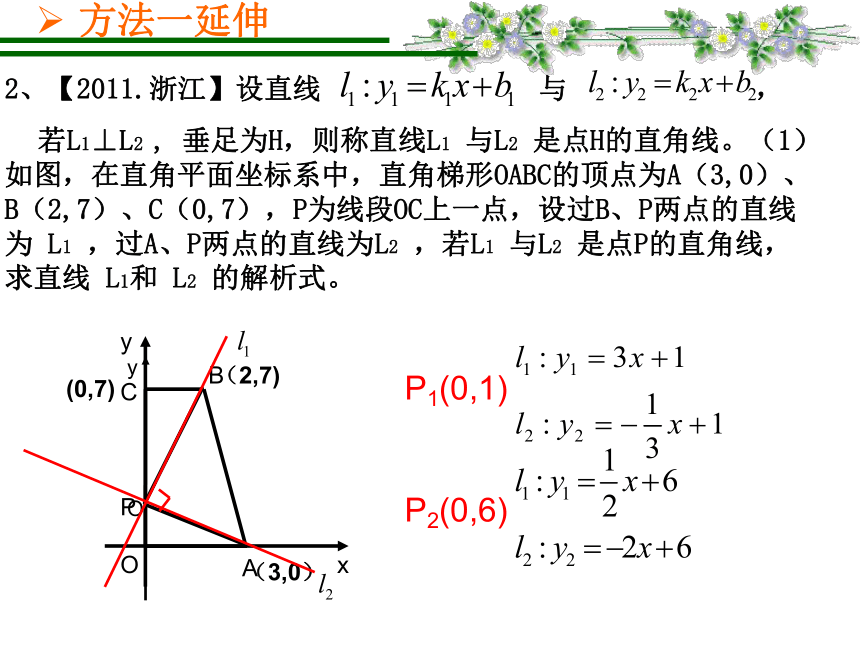
角形时,求点P的坐标.P1P2(4,3)PP3 (1,0) P4 (3,0)综上所述:GF方法一延伸P1(0,1)P2(0,6)O(3,0)(2,7)(0,7)方法一延伸3、(2012温州中考24 )如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP. 1)当m=3时,求点A的坐标及BC的长; 2)当m>1时,连接CA,
问m为何值时CA⊥CP?
3)过点P作PE⊥PC且PE=PC,问是否
存在m,使得点E落在坐标轴上?若存
在,求出所有满足要求的m的值,并
求出相对应的点E坐标;若不存在,
请说明理由.
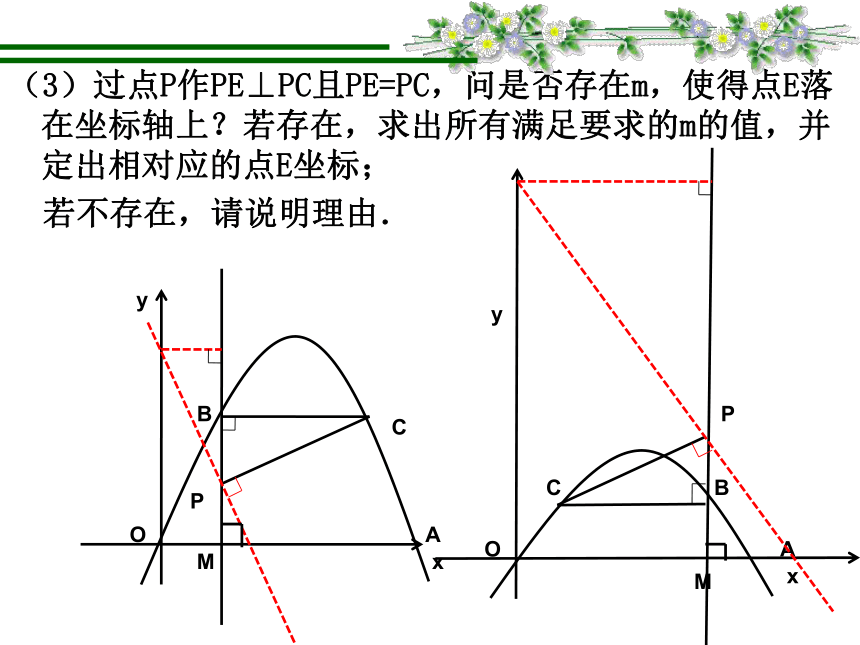
方法一延伸(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;
若不存在,请说明理由.
xyOBCAPMxyOBCAPM02-2xyy=xy=x+2y=x-2直线的平移:
k不变, b 变了.直线平行:
k相同,b不同.A(2,2)A(2,-4)y=x-6(平行直线可以由原直线上下平移得到,
平移距离=线上对应点的竖直移动距离)方法专题二例2、如图,抛物线解析式为 ,
顶点为B,过点A(2,5)往x轴作垂线,
与抛物线交于P点,
①求直线AB的解析式;③抛物线上是否存在点Q(不同P点),使得?ABQ与?ABP的面积相同,若存在,求出所有的Q点坐标,若不存在,请说明理由。②求?ABP的面积;1、如图,已知抛物线 的图像与
x轴交于A(- ,0),B(2,0)两点,与y轴交于点C;
①判断?ABC的形状;②此抛物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出点P的坐标;若不存在,说明理由。ACBmnDE2、如图,已知二次函数 的
图像与y轴交于点C,与x轴交于A,B(A在B的左侧),连接AC。
①求AC的直线解析式;②点P为x轴下方的抛物线上的一个动点,连接PA、PC,记?PAC的面积为S,问S取何值时,相应的P有且只有两个?ACBP例3 如图,O为坐标原点,有一个矩形OABC, C(10,0)、A(0,4), M是线段OC的中点,在AB上有一个动点P,使得
△POM是一个等腰三角形
求P点坐标.方法专题三1、如图, 直角梯形ABCD中,AD∥BC,∠C=90°, BC=16cm,DC=12cm, AD=21cm. 动点P从D出发,沿射线DA的方向以每秒2cm的速度运动,动点Q从点C出发,在线段CB上以1cm每秒的速度向点B运动,点P、Q分别从D、C同时出发,当点Q运动到点B时,点P随之停止运动.设运动时间为t(秒).
当t为何值时,△BPQ的
面积为60c㎡;
2) 当t为何值时,以B,P,Q三点为顶点
的三角形是等腰三角形.E2、如图,Rt△ABC中,∠C=90°,BC=6,AC=8.
点P,Q都是斜边AB上的动点,点P从B向A运动
(不与点B重合),点Q从A向B运动,BP=AQ.点
D、E分别是点A、B以Q、P为对称中心的对称点HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,
P、Q同时停止运动.
设BP的长为x.
1)图中与BP相等的线段有哪些?
2)当x为何值时,△HDE为
等腰三角形?
ED= 10 -4X DE= 4X-102)当x为何值时,△HDE为等腰三角形?3、如图,已知一次函数y =-x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
1)求点A和点B的坐标;
2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,
直线l交x轴于点R,交线段BA或线段
AO于点Q.当点P到达点A时,点P和
直线l都停止运动.在运动过程中,
设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.谢谢大家,请予指正!
------谈初中数学专题复习课
问题: 学生做题不能触类旁通,做过的题目稍作变化后就又不会做了,教师对每个大题都得一一讲解,而效果却不尽人意。主要原因:①对数学知识之间的联系缺乏认识;
②对题目考查的数学本质不清楚;
③做题只为做题,没有反思归纳;
解决问题
所以开展专题复习课,学一题解一类,安排有一定的系统性,针对性,串联性的解题训练,让散落的珍珠串成美丽的项链,既能帮助学生从题海中走出来,又可以有效提高总复习的效率。O(0,2)(2,3)(3,1) 例1:如图,直线AB:y=-2x+2 交与x轴于点A,交与y轴于点B,以AB为边在第一象限内作正方形ABCD,求过B、C、D三点的抛物线的解析式.方法专题一ACBEDACBED 1、 如图,直线 与y轴交于点A,与x轴交于点D,
抛物线 与直线交于A,E两点,与x轴交于
B,C两点,且B点坐标为(1,0).
уχ(0,1)(1)求抛物线的解析式;(2)动点P在x轴上移动,以 P、
A、E为顶点的三角形是直角三
角形时,求点P的坐标.P1P2(4,3)PP3 (1,0) P4 (3,0)综上所述:GF方法一延伸P1(0,1)P2(0,6)O(3,0)(2,7)(0,7)方法一延伸3、(2012温州中考24 )如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP. 1)当m=3时,求点A的坐标及BC的长; 2)当m>1时,连接CA,
问m为何值时CA⊥CP?
3)过点P作PE⊥PC且PE=PC,问是否
存在m,使得点E落在坐标轴上?若存
在,求出所有满足要求的m的值,并
求出相对应的点E坐标;若不存在,
请说明理由.
方法一延伸(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;
若不存在,请说明理由.
xyOBCAPMxyOBCAPM02-2xyy=xy=x+2y=x-2直线的平移:
k不变, b 变了.直线平行:
k相同,b不同.A(2,2)A(2,-4)y=x-6(平行直线可以由原直线上下平移得到,
平移距离=线上对应点的竖直移动距离)方法专题二例2、如图,抛物线解析式为 ,
顶点为B,过点A(2,5)往x轴作垂线,
与抛物线交于P点,
①求直线AB的解析式;③抛物线上是否存在点Q(不同P点),使得?ABQ与?ABP的面积相同,若存在,求出所有的Q点坐标,若不存在,请说明理由。②求?ABP的面积;1、如图,已知抛物线 的图像与
x轴交于A(- ,0),B(2,0)两点,与y轴交于点C;
①判断?ABC的形状;②此抛物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出点P的坐标;若不存在,说明理由。ACBmnDE2、如图,已知二次函数 的
图像与y轴交于点C,与x轴交于A,B(A在B的左侧),连接AC。
①求AC的直线解析式;②点P为x轴下方的抛物线上的一个动点,连接PA、PC,记?PAC的面积为S,问S取何值时,相应的P有且只有两个?ACBP例3 如图,O为坐标原点,有一个矩形OABC, C(10,0)、A(0,4), M是线段OC的中点,在AB上有一个动点P,使得
△POM是一个等腰三角形
求P点坐标.方法专题三1、如图, 直角梯形ABCD中,AD∥BC,∠C=90°, BC=16cm,DC=12cm, AD=21cm. 动点P从D出发,沿射线DA的方向以每秒2cm的速度运动,动点Q从点C出发,在线段CB上以1cm每秒的速度向点B运动,点P、Q分别从D、C同时出发,当点Q运动到点B时,点P随之停止运动.设运动时间为t(秒).
当t为何值时,△BPQ的
面积为60c㎡;
2) 当t为何值时,以B,P,Q三点为顶点
的三角形是等腰三角形.E2、如图,Rt△ABC中,∠C=90°,BC=6,AC=8.
点P,Q都是斜边AB上的动点,点P从B向A运动
(不与点B重合),点Q从A向B运动,BP=AQ.点
D、E分别是点A、B以Q、P为对称中心的对称点HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,
P、Q同时停止运动.
设BP的长为x.
1)图中与BP相等的线段有哪些?
2)当x为何值时,△HDE为
等腰三角形?
ED= 10 -4X DE= 4X-102)当x为何值时,△HDE为等腰三角形?3、如图,已知一次函数y =-x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
1)求点A和点B的坐标;
2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,
直线l交x轴于点R,交线段BA或线段
AO于点Q.当点P到达点A时,点P和
直线l都停止运动.在运动过程中,
设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.谢谢大家,请予指正!
同课章节目录
