北师大版数学八年级上册同步课时练习:第7章 平行线的证明4 平行线的性质 (word版含答案)
文档属性
| 名称 | 北师大版数学八年级上册同步课时练习:第7章 平行线的证明4 平行线的性质 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 147.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览



文档简介
4 平行线的性质
知识点 平行线的性质
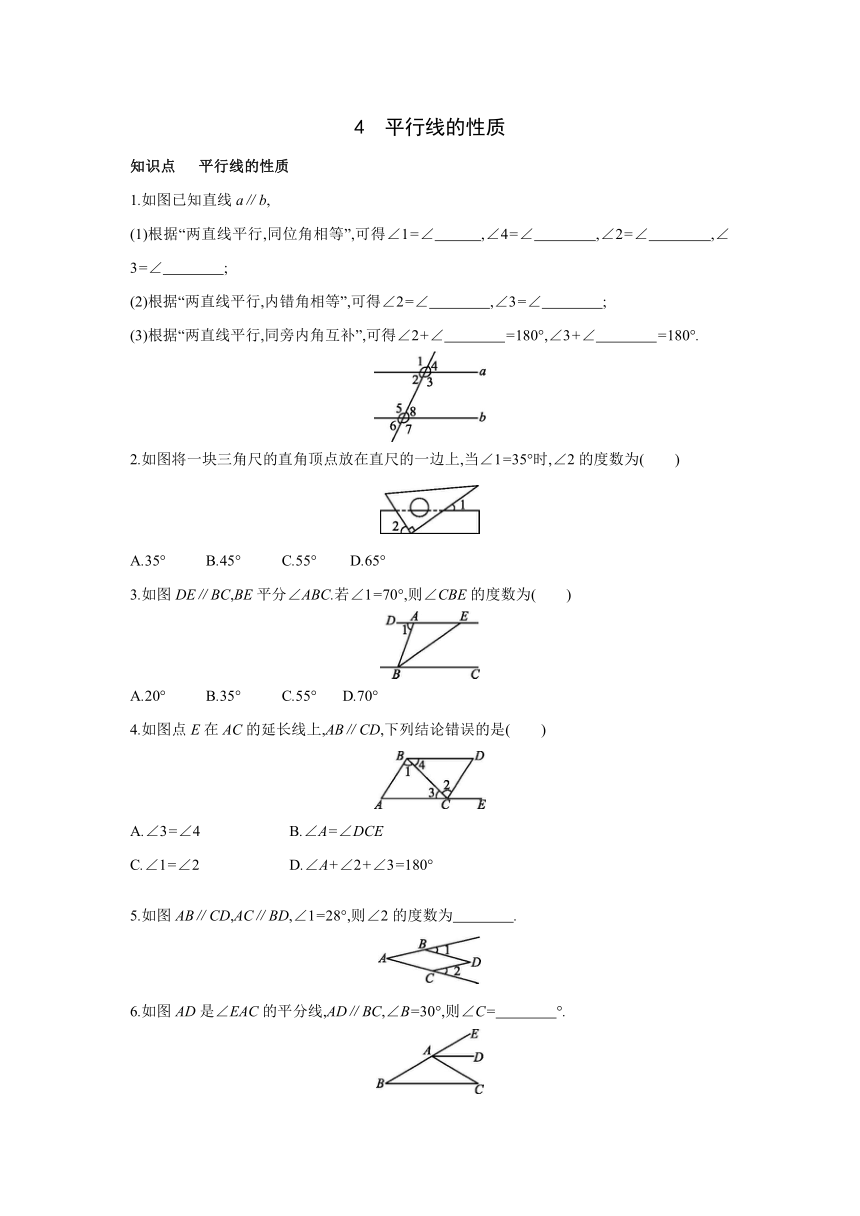
1.如图已知直线a∥b,
(1)根据“两直线平行,同位角相等”,可得∠1=∠ ,∠4=∠ ,∠2=∠ ,∠3=∠ ;
(2)根据“两直线平行,内错角相等”,可得∠2=∠ ,∠3=∠ ;
(3)根据“两直线平行,同旁内角互补”,可得∠2+∠ =180°,∠3+∠ =180°.
2.如图将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45° C.55° D.65°
3.如图DE∥BC,BE平分∠ABC.若∠1=70°,则∠CBE的度数为( )
A.20° B.35° C.55° D.70°
4.如图点E在AC的延长线上,AB∥CD,下列结论错误的是( )
A.∠3=∠4 B.∠A=∠DCE
C.∠1=∠2 D.∠A+∠2+∠3=180°
5.如图AB∥CD,AC∥BD,∠1=28°,则∠2的度数为 .
6.如图AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C= °.
7.填空:如图示.
因为DF∥AC(已知),所以∠D+ =180°( ).
因为∠C=∠D(已知),所以∠C+ =180°( ),
所以DB∥EC( ).
8.如图已知AE∥BC,且∠B=∠C.求证:AE平分∠DAC.
9.如图直线AB∥CD,BC平分∠ABD,∠1=54°.
求:(1)∠ABD的度数;
(2)∠2的度数.
10.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,连接AC,BC.若∠ABC=54°,则∠1的度数为( )
A.36° B.54° C.60° D.72°
11.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是
( )
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DBO不相等
12.光线在不同介质中的传播速度不同,因此,当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,折射后在空气中也是平行的.若水面和杯底是相互平行的,且∠1=45°,∠2=122°,则∠3= °,∠4= °.
13.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C',D'处,C'E交AF于点G.若∠CEF=70°,则∠GFD'= °.
14.如图,已知CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,则直线EF与AB有怎样的位置关系 为什么
15.[教材习题7.5第3题变式] 学行线的性质》后,老师为了帮同学们巩固平行线的性质,在黑板上出了这样一道题:
如图,AB∥CD,AD∥BC.
(1)求∠A+∠B+∠C+∠D的度数;
(2)用三种不同的方法证明∠A=∠C.
请你用平行线的性质来解决以上问题.
16.如图(a),E是直线AB,CD之间一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度
②若∠A=20°,∠AED=80°,则∠D等于多少度
③猜想图(a)中∠AED,∠A,∠D之间的数量关系,并证明你的结论.
(2)拓展应用:
如图图(b),射线FE与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④是被射线FE隔开的4个区域(不含边界,其中区域③④位于直线AB上方),P是位于以上四个区域内的点,猜想:∠PEB,∠PFC,∠EPF之间的关系(不要求证明).
答案
1.(1)5 8 6 7 (2)8 5 (3)5 8
2.C 3.B 4.A
5.28° 6.30
7.∠DBC 两直线平行,同旁内角互补 ∠DBC等量代换 同旁内角互补,两直线平行
8.证明:∵AE∥BC(已知),∴∠DAE=∠B(两直线平行,同位角相等),
∠CAE=∠C(两直线平行,内错角相等).又∵∠B=∠C(已知),
∴∠DAE=∠CAE(等量代换),∴AE平分∠DAC(角平分线的定义).
9.解:(1)∵AB∥CD(已知),∴∠ABC=∠1=54°(两直线平行,内错角相等).
∵BC平分∠ABD(已知),∴∠ABD=2∠ABC=2×54°=108°(角平分线的定义).
(2)∵AB∥CD,∴∠ABD+∠CDB=180°.又∵∠ABD=108°,∴∠CDB=180°-108°=72°,
∴∠2=∠CDB=72°.
10.D ∵直线l1∥l2,∴∠1+∠ACB+∠ABC=180°.∵∠ABC=54°,AC=AB,∴△ABC为等腰三角形,∴∠ABC=∠ACB=54°,∴∠1=72°.
11.D 因为AC∥BD,所以∠BAC+∠ABD=180°.因为AO,BO分别是∠BAC,∠ABD的平分线,所以∠BAO与∠CAO相等,∠ABO与∠DBO相等,所以∠BAO与∠ABO互余.故选D.
12.45 58
13.40 因为四边形ABCD是长方形,所以AD∥BC,所以∠GFE=∠CEF=70°,∠CEF+∠EFD=180°,所以∠EFD=110°.由折叠可知∠EFD'=∠EFD=110°,故∠GFD'=∠EFD'-∠GFE=110°-70°=40°.
故答案为40.
14.解:EF∥AB.理由如图下:因为CD∥AB,∠DCB=70°,所以∠DCB=∠ABC=70°.
因为∠CBF=20°,所以∠ABF=∠ABC-∠CBF=50°.因为∠EFB=130°,
所以∠ABF+∠EFB=50°+130°=180°,所以EF∥AB.
15.解:(1)∵AD∥BC,∴∠A+∠B=180°,∠C+∠D=180°,
∴∠A+∠B+∠C+∠D=180°+180°=360°.
(2)证明:①∵AD∥BC,∴∠A+∠B=180°.∵AB∥CD,∴∠C+∠B=180°,∴∠A=∠C.
②如图图(a),延长AB到点E.∵AD∥BC,∴∠A=∠CBE.
∵AB∥CD,∴∠C=∠CBE,∴∠A=∠C.
③如图图(b),连接AC.∵AD∥BC,∴∠DAC=∠ACB.∵AB∥CD,∴∠BAC=∠ACD,
∴∠DAC+∠BAC=∠ACB+∠ACD,∴∠BAD=∠BCD.(答案不唯一)
16.解:(1)①∠AED=70°.②∠D=60°.③猜想:∠AED=∠A+∠D.
证明:如图图,作射线EF∥AB,所以∠AEF=∠A.因为AB∥CD,所以EF∥CD.所以∠FED=∠D.
所以∠AED=∠AEF+∠FED=∠A+∠D.
(2)若点P在区域①,则∠EPF=360°-(∠PEB+∠PFC);若点P在区域②,则∠EPF=∠PEB+∠PFC;若点P在区域③,则∠EPF=∠PEB-∠PFC;若点P在区域④,则∠EPF=∠PFC-∠PEB.
知识点 平行线的性质
1.如图已知直线a∥b,
(1)根据“两直线平行,同位角相等”,可得∠1=∠ ,∠4=∠ ,∠2=∠ ,∠3=∠ ;
(2)根据“两直线平行,内错角相等”,可得∠2=∠ ,∠3=∠ ;
(3)根据“两直线平行,同旁内角互补”,可得∠2+∠ =180°,∠3+∠ =180°.
2.如图将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45° C.55° D.65°
3.如图DE∥BC,BE平分∠ABC.若∠1=70°,则∠CBE的度数为( )
A.20° B.35° C.55° D.70°
4.如图点E在AC的延长线上,AB∥CD,下列结论错误的是( )
A.∠3=∠4 B.∠A=∠DCE
C.∠1=∠2 D.∠A+∠2+∠3=180°
5.如图AB∥CD,AC∥BD,∠1=28°,则∠2的度数为 .
6.如图AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C= °.
7.填空:如图示.
因为DF∥AC(已知),所以∠D+ =180°( ).
因为∠C=∠D(已知),所以∠C+ =180°( ),
所以DB∥EC( ).
8.如图已知AE∥BC,且∠B=∠C.求证:AE平分∠DAC.
9.如图直线AB∥CD,BC平分∠ABD,∠1=54°.
求:(1)∠ABD的度数;
(2)∠2的度数.
10.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,连接AC,BC.若∠ABC=54°,则∠1的度数为( )
A.36° B.54° C.60° D.72°
11.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是
( )
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DBO不相等
12.光线在不同介质中的传播速度不同,因此,当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,折射后在空气中也是平行的.若水面和杯底是相互平行的,且∠1=45°,∠2=122°,则∠3= °,∠4= °.
13.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C',D'处,C'E交AF于点G.若∠CEF=70°,则∠GFD'= °.
14.如图,已知CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,则直线EF与AB有怎样的位置关系 为什么
15.[教材习题7.5第3题变式] 学行线的性质》后,老师为了帮同学们巩固平行线的性质,在黑板上出了这样一道题:
如图,AB∥CD,AD∥BC.
(1)求∠A+∠B+∠C+∠D的度数;
(2)用三种不同的方法证明∠A=∠C.
请你用平行线的性质来解决以上问题.
16.如图(a),E是直线AB,CD之间一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度
②若∠A=20°,∠AED=80°,则∠D等于多少度
③猜想图(a)中∠AED,∠A,∠D之间的数量关系,并证明你的结论.
(2)拓展应用:
如图图(b),射线FE与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④是被射线FE隔开的4个区域(不含边界,其中区域③④位于直线AB上方),P是位于以上四个区域内的点,猜想:∠PEB,∠PFC,∠EPF之间的关系(不要求证明).
答案
1.(1)5 8 6 7 (2)8 5 (3)5 8
2.C 3.B 4.A
5.28° 6.30
7.∠DBC 两直线平行,同旁内角互补 ∠DBC等量代换 同旁内角互补,两直线平行
8.证明:∵AE∥BC(已知),∴∠DAE=∠B(两直线平行,同位角相等),
∠CAE=∠C(两直线平行,内错角相等).又∵∠B=∠C(已知),
∴∠DAE=∠CAE(等量代换),∴AE平分∠DAC(角平分线的定义).
9.解:(1)∵AB∥CD(已知),∴∠ABC=∠1=54°(两直线平行,内错角相等).
∵BC平分∠ABD(已知),∴∠ABD=2∠ABC=2×54°=108°(角平分线的定义).
(2)∵AB∥CD,∴∠ABD+∠CDB=180°.又∵∠ABD=108°,∴∠CDB=180°-108°=72°,
∴∠2=∠CDB=72°.
10.D ∵直线l1∥l2,∴∠1+∠ACB+∠ABC=180°.∵∠ABC=54°,AC=AB,∴△ABC为等腰三角形,∴∠ABC=∠ACB=54°,∴∠1=72°.
11.D 因为AC∥BD,所以∠BAC+∠ABD=180°.因为AO,BO分别是∠BAC,∠ABD的平分线,所以∠BAO与∠CAO相等,∠ABO与∠DBO相等,所以∠BAO与∠ABO互余.故选D.
12.45 58
13.40 因为四边形ABCD是长方形,所以AD∥BC,所以∠GFE=∠CEF=70°,∠CEF+∠EFD=180°,所以∠EFD=110°.由折叠可知∠EFD'=∠EFD=110°,故∠GFD'=∠EFD'-∠GFE=110°-70°=40°.
故答案为40.
14.解:EF∥AB.理由如图下:因为CD∥AB,∠DCB=70°,所以∠DCB=∠ABC=70°.
因为∠CBF=20°,所以∠ABF=∠ABC-∠CBF=50°.因为∠EFB=130°,
所以∠ABF+∠EFB=50°+130°=180°,所以EF∥AB.
15.解:(1)∵AD∥BC,∴∠A+∠B=180°,∠C+∠D=180°,
∴∠A+∠B+∠C+∠D=180°+180°=360°.
(2)证明:①∵AD∥BC,∴∠A+∠B=180°.∵AB∥CD,∴∠C+∠B=180°,∴∠A=∠C.
②如图图(a),延长AB到点E.∵AD∥BC,∴∠A=∠CBE.
∵AB∥CD,∴∠C=∠CBE,∴∠A=∠C.
③如图图(b),连接AC.∵AD∥BC,∴∠DAC=∠ACB.∵AB∥CD,∴∠BAC=∠ACD,
∴∠DAC+∠BAC=∠ACB+∠ACD,∴∠BAD=∠BCD.(答案不唯一)
16.解:(1)①∠AED=70°.②∠D=60°.③猜想:∠AED=∠A+∠D.
证明:如图图,作射线EF∥AB,所以∠AEF=∠A.因为AB∥CD,所以EF∥CD.所以∠FED=∠D.
所以∠AED=∠AEF+∠FED=∠A+∠D.
(2)若点P在区域①,则∠EPF=360°-(∠PEB+∠PFC);若点P在区域②,则∠EPF=∠PEB+∠PFC;若点P在区域③,则∠EPF=∠PEB-∠PFC;若点P在区域④,则∠EPF=∠PFC-∠PEB.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
