第五章中心对称图形 圆专题复习

课件27张PPT。１、圆的基本元素: 圆心、半径。一、知识点：２、圆的对称性: 圆的旋转对称性、圆是中心对称图形、圆是轴对称图形。3、圆周角、圆心角、弦的关系:
定理:在同圆或等圆中,相等的圆心角所对的弧相等, 所对的弦、也相等。
推论:在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它 们所对应的其余各组量都分别相等。4、过三点的圆:
(1)定理:不在同一直线上的三点确定一个圆。
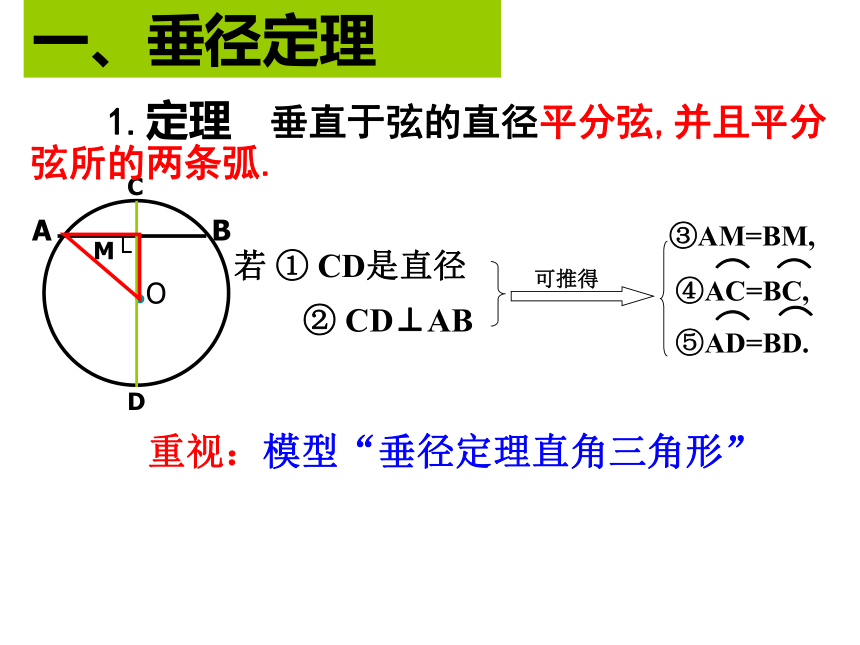
(2)三角形的外接圆的圆心是三边的垂直平分线的交点。5、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。一、垂径定理③AM=BM,重视：模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB　　1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.例⊙O的半径为10cm，弦AB∥CD，
AB=16，CD=12，则AB、CD间的
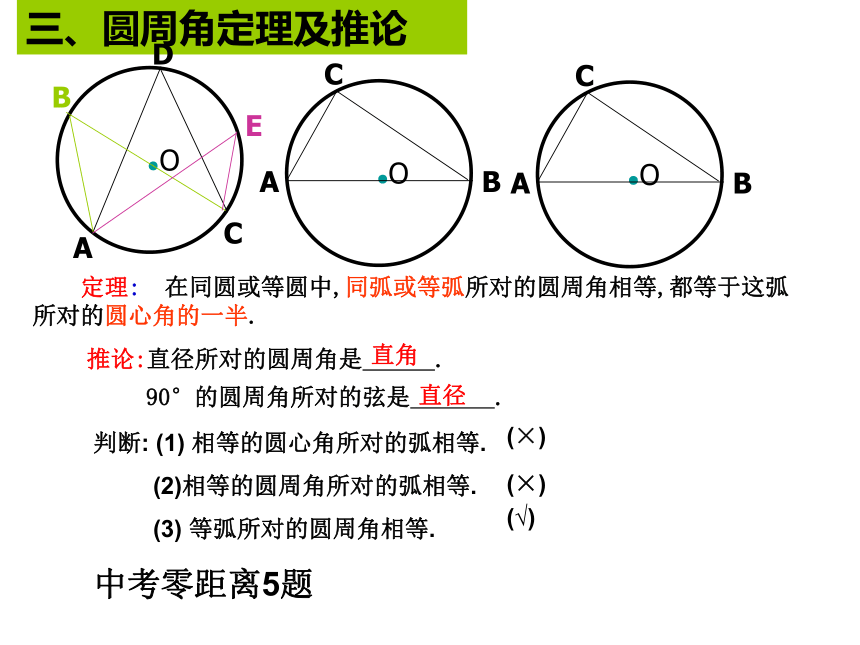
距离是___ .2cm或14cm中考零距离2、6题ABCP2、 如图，AB是⊙O的任意一条弦，OC⊥AB，垂足为P，若 CP=7cm，AB=28cm ，你能帮老师求出这面镜子的半径吗？O714综合应用垂径定理和勾股定理可求得半径 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′①∠AOB=∠A′O′B′二、圆心角、弧、弦的关系三、圆周角定理及推论 90°的圆周角所对的弦是 . 定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.(×)(×)(√)中考零距离5题1.如图：圆O中弦AB等于半径R，则这条弦所对的圆心角是＿＿＿,圆周角是＿＿＿＿＿＿.60度30或150度　2：已知ABC三点在圆O上，连接ABCO，如果∠ AOC=140 °，求∠ B的度数．　3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.D　　解：在优弧AC上定一点D，连结AD、
CD.
∵ ∠ AOC=140 °
∴ ∠ D=70 °
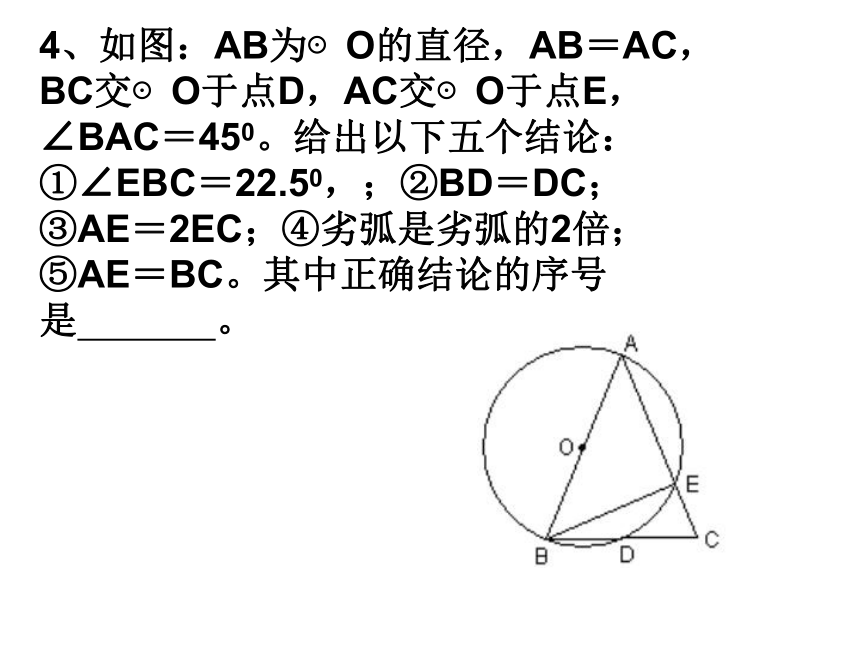
∴ ∠ B=180 ° －70 ° =110 °2或4cm4、如图：AB为⊙O的直径，AB＝AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC＝450。给出以下五个结论： ①∠EBC＝22.50，；②BD＝DC； ③AE＝2EC；④劣弧是劣弧的2倍； ⑤AE＝BC。其中正确结论的序号是 。 一：点与圆的位置关系d﹥rd=rd﹤r点到圆心的距离d与圆的半径r
之间关系
二：直线与圆的位置关系lllＡ直线l叫做＿＿＿　　　直线l叫做＿＿＿
点Ａ叫做＿＿＿　　　d﹥rd=rd﹤r0１２割线切线切点交点个数 名称外离1外切1内含d > R + rd = R + rR-r< d < R+ rd = R - rd < R - rd与Ｒ,r的关系对称性三：圆与圆的位置关系
都是轴对称图形，其对称轴是：两圆连心线结论：相切时，切点在连心线上同心圆是内含的特殊情况1、已知⊙O的半径为r，圆心O到直线l的距
离为d。若直线L与⊙O有交点，则下列结
论中正确的是（ ）A. d=r B. d≤r C.d≥r D.d＜rB2、两圆有多种位置关系，图中不
存在的位置关系是 ． 内切3. ⊙O1和⊙O2的半径分别为R1 和R2 ，
圆心距O1O2=5，R1=3，当0＜R2＜2时，
⊙O1和⊙O2的位置关系是（ ）A.内含 B.外切 C.相交 D.外离D4. 已知⊙A和⊙B相切，两圆的圆心距为8cm，
⊙A的半径为3cm，则⊙B半径是（ ）A.5cm B.11cm C.3cm D. 5cm或11cmD中考零距离7、8题切线的性质定理圆的切线垂直于过切点的半径.
∵CD切⊙O于Ａ, OA是⊙O的半径CD●OA∴CD⊥OA.中考零距离1、9题切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.CD●OA　
　∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.切线的判定定理的两种应用　　1、如果已知直线与圆有交点，往往要作出过这一点的半径，再证明直线垂直于这条半径即可；
　　2、如果不明确直线与圆的交点，往往要作出圆心到直线的垂线段，再证明这条垂线段等于半径即可．　1、如图,AB是圆O的直径,圆O过AC的中点D,

DE⊥BC于E．求证:DE是圆O的切线.
　　证明：连接OD证OD⊥DE２．如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。
求证：（1）AC是⊙D的切线；
（2）AB+EB=AC。证明：过点D作DF⊥AC,
垂足是F证DF=DB ,
即DB是圆D的半径ABCO七.三角形的外接圆和内切圆：ABCI三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.三角形的外心是否一定在三角形的内部？从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.切线长定理及其推论:直角三角形的内切圆半径与三边关系.三角形的内切圆半径与圆面积.∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2② r=ab ÷(a+b+c)2. 正三角形的边长为2a,它的内切圆和
外接圆的半径分别是______ , ____（05大连）
1、边长分别为3,4,5的三角形的内切圆半径与外接圆半径的比为( )

A.1∶5 B.2∶5 C.3∶5 D.4∶5B4．如图4，⊙M与x轴相交于点A（2，0），　　B（8，0），
与y轴相切于点C，求圆心M的坐标．3.在直角三角形ABC中, ∠C=Rt∠,
AC=6,BC=8,则其外接圆半径=___,
内切圆半径=___.
52M(5 , 3 )　　1、如图1，AB是⊙O的直径，C为圆上一点，弧AC度数为60°，OD⊥BC，D为垂足，且OD=10，则AB=_____，BC=_____；
　　2、已知、是同圆的两段弧，且弧AB等于2倍弧AC，则弦AB与CD之间的关系为（ ）；
　A.AB=2CD B.AB<2CD C.AB>2CD D.不能确定
　　3、 如图2，⊙O中弧AB的度数为60°，AC是⊙O的直径，那么∠BOC等于 ( )；
　A．150° B．130° C．120° D．60°
　　4、在△ABC中，∠A＝70°，若O为△ABC的外心，∠BOC= 　；若O为△ABC的内心，∠BOC= 　．
　　　　　　　　　　　　图1　　　　　　　　　　　　　图220BC1400125010√31.在Rt△ ABC中，∠C=90°,BC=3cm,
AC=4cm,D为AB的中点，E为AC的中点，
以B为圆心，BC为半径作⊙B，问：
（1）A、C、D、E与⊙B的位置关系如何？
（2）AB、AC与⊙B的位置关系如何？如图，AB是⊙O的弦，OC⊥OA交AB于点C，过点B的直线交OC的延长线于点E，当CE=BE时，直线BE与⊙O有怎样的位置关系？并证明你的结论．