11.5 几何证明举例（3）(教案)

学科
数学
年级
八
时间

总序号
?
课题
?
11.5 几何证明举例（第3课时）
主备人

授课人

教学目标
和
学习目标
1. 会根据三角形全等推导等腰三角形的性质。；
2. 熟练掌握应用等腰三角形的性质和判定定理；
3. 掌握等边三角形的性质，并会运用其性质解决相关问题；
4.逐步学习用数学符号与语言来规范表述证明过程
教学重点
教学难点
?
重点：会用全等三角形判定和性质定理、同一三角形中“等边对等角”
及适当添置辅助线创设条件证明边相等和角相等。
难点：证明思路和过程的寻求及规范的证明格式书写。
师
生
互
动
过
程
教学内容和学生活动
教师活动
?
一．情境导入：
　同学们运用你手中的三角板，你可以拼出等腰三角形吗，通过拼出的三角形你会发现那些问题呢？
（二）探究新知：
1.问题导读：
（1）“等腰三角形的两个底角相等”是真命题吗？怎样证明。
（2）在右图等腰△ABC中，AB=AC.AD为BC边上的高
∠1与∠2有什么关系？BD与CD有什么关系？
你能得出什么结论？试着总结一下。
（3）说出命题“等腰三角形的两个底角相等”的逆命题？
（4）这个逆命题是真命题吗？怎样证明它的正确性？
?设置这一实践活动，让学生在实践中发现、提出问题，解决问题，有利于激发学生的学习兴趣，培养学生的探究意识，培养学生发现问题解决问题的能力。
师
生
互
动
过
程
教学内容和学生活动
教师活动
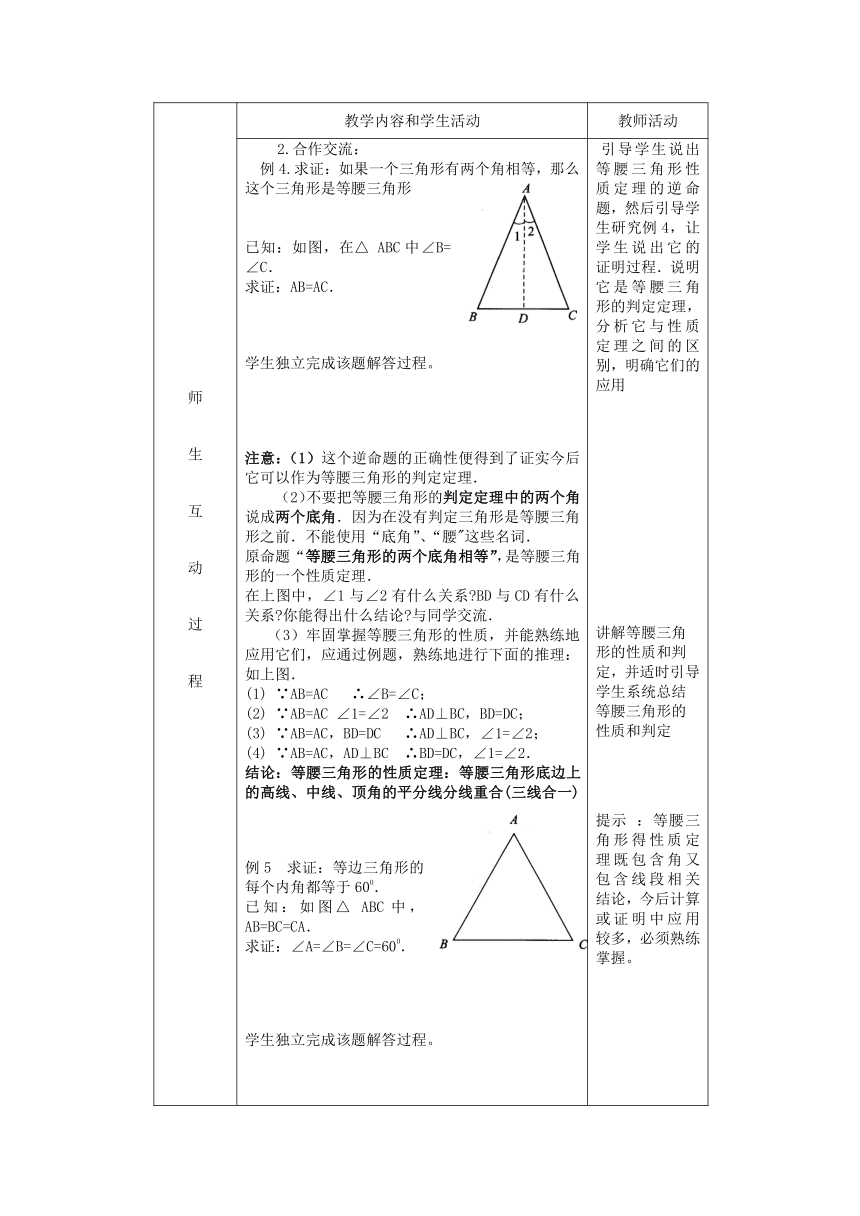
?2.合作交流：
例4.求证：如果一个三角形有两个角相等，那么这个三角形是等腰三角形
已知：如图，在△ ABC中∠B=∠C．
求证：AB=AC．
学生独立完成该题解答过程。
注意：（1）这个逆命题的正确性便得到了证实今后它可以作为等腰三角形的判定定理．
（2）不要把等腰三角形的判定定理中的两个角说成两个底角．因为在没有判定三角形是等腰三角形之前．不能使用“底角”、“腰"这些名词．
原命题“等腰三角形的两个底角相等”，是等腰三角形的一个性质定理．
在上图中，∠1与∠2有什么关系?BD与CD有什么关系?你能得出什么结论?与同学交流．
（3）牢固掌握等腰三角形的性质，并能熟练地应用它们，应通过例题，熟练地进行下面的推理：如上图．
(1) ∵AB=AC ∴∠B=∠C；
(2) ∵AB=AC ∠1=∠2 ∴AD⊥BC，BD=DC；
(3) ∵AB=AC，BD=DC ∴AD⊥BC，∠1=∠2；
(4) ∵AB=AC，AD⊥BC ∴BD=DC，∠1=∠2．
结论：等腰三角形的性质定理：等腰三角形底边上的高线、中线、顶角的平分线分线重合(三线合一)
例5 求证：等边三角形的每个内角都等于600．
已知：如图△ ABC中，AB=BC=CA．
求证：∠A=∠B=∠C=600．
学生独立完成该题解答过程。
?引导学生说出等腰三角形性质定理的逆命题，然后引导学生研究例4，让学生说出它的证明过程．说明它是等腰三角形的判定定理，分析它与性质定理之间的区别，明确它们的应用
讲解等腰三角形的性质和判定，并适时引导学生系统总结等腰三角形的性质和判定
提示 ：等腰三角形得性质定理既包含角又包含线段相关结论，今后计算或证明中应用较多，必须熟练掌握。
师
生
互
动
过
程
教学内容和学生活动
教师活动
?
三、跟踪训练： 看我有多棒！
1．已知：如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E，F
求证：DE=DF．
2．求证：等腰三角形两底角的平分线相等．
四．课堂小结
通过本节课的学习,我掌握了_____________
最满意的是_________________________
需再努力的是______________________
五、作业布置：
1、习题11.5 第6-10题
?
巡视指导，反馈信息，掌握学生学习情况
板 书 设 计
11.5几何证明举例三
1、等腰三角形的判定定理：
2、等呀三角形的性质定理
3、等边三角形的性质定理与判定定理