湘教版数学七年级下册 4.4 平行线的判定1第1课时 平行线的判定方法1课件(共22张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 4.4 平行线的判定1第1课时 平行线的判定方法1课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 834.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
4.4 平行线的判定
第4章 相交线与平行线
第1课时 平行线的判定方法1
1.会运用同位角相等判定两条直线平行;
2.会综合运用平行线的判定和性质解题.(难点)
学习目标
A
B
C
D
M
N
在练习本上画两条平行线AB、CD,再画直线MN与直线AB,CD相交(如下图)
任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?由此你能得到什么结论?
3
4
1
5
2
6
8
7
导入新课
情境引入
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
情境导入
想一想:
生活中的问题能用数学知识解决吗?
a
b
c
如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线 a和b平行
③直线a和b不平行
做一做
●
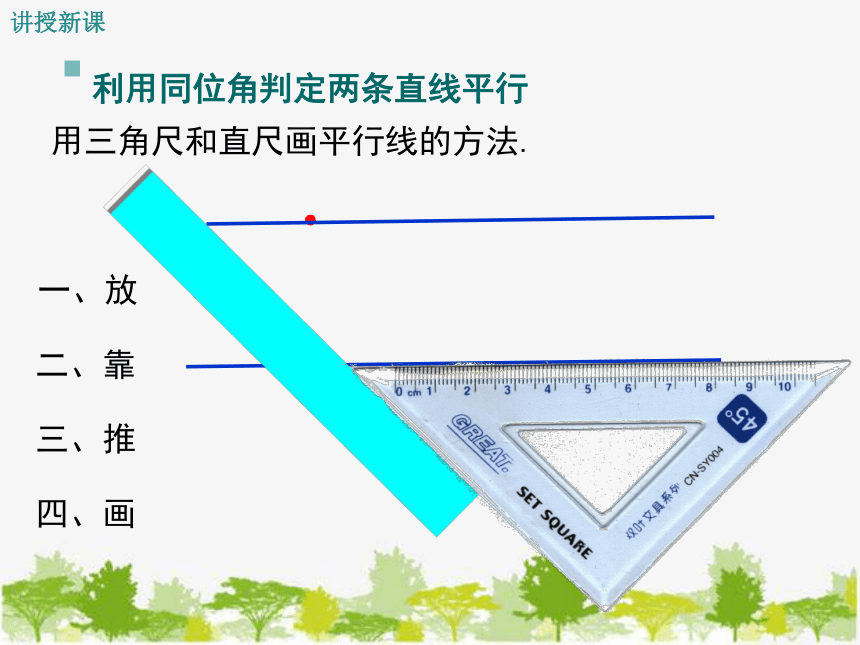
一、放
二、靠
三、推
四、画
用三角尺和直尺画平行线的方法.
利用同位角判定两条直线平行
讲授新课
●
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
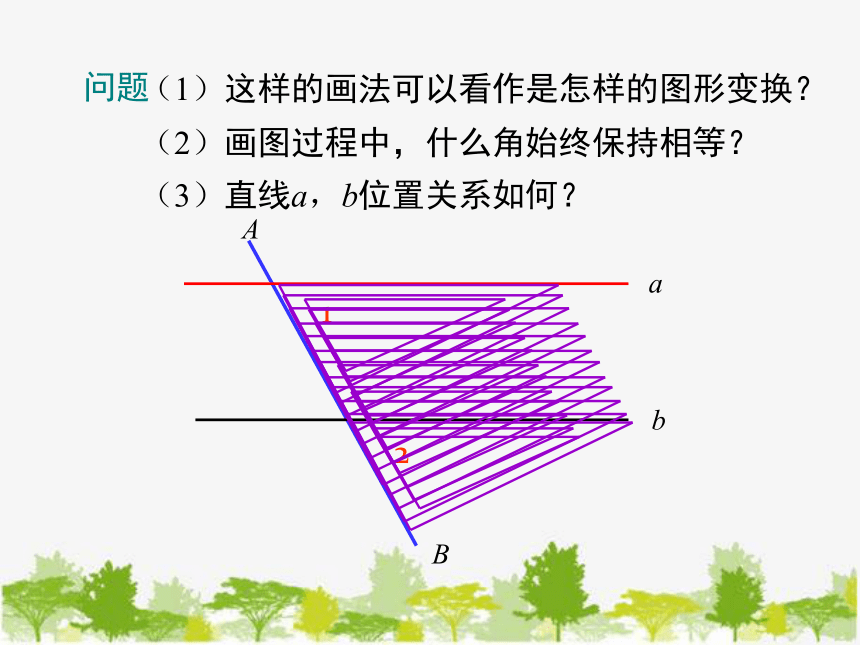
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线a,b位置关系如何?
问题
(4)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的
方法吗?
判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2 (同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
练习:下图中若∠1=550 ,∠2=550,直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
同位角相等,两直线平行.
变式1:
如图, ∠1=55 , ∠2=125 ,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
同位角相等,两直线平行.
变式2:
如图, 直线AB与CD被直线EF所截,∠1=55 ,请添加一个条件使得直线AB与直线CD平行.
A
C
E
F
B
D
1
3
2
5
4
∠5=55
你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?
练一练
例1 如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解析:根据AB∥DC及∠D=125°,可求出∠A的度数,从而说明∠A=∠CBE.再根据同位角相等,两直线平行可得AD∥BC.
B
A
D
C
E
解:AD∥BC.
理由如下:因为AB∥DC(已知),
所以∠A+∠D=180°(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D=180°-125°=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE,所以AD∥BC
(同位角相等,两直线平行).
1.从∠5=∠ ,可以推出AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
当堂练习
2.如图所示,已知直线EF和AB,CD分别
相交于K,H,且∠EGB=90°,∠CHF=60°,
∠E=30°,试说明AB∥CD.
解:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
由同位角的关系判断两直线平行的三个步骤:
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.
课堂小结
见对应习题。
课后作业
4.4 平行线的判定
第4章 相交线与平行线
第1课时 平行线的判定方法1
1.会运用同位角相等判定两条直线平行;
2.会综合运用平行线的判定和性质解题.(难点)
学习目标
A
B
C
D
M
N
在练习本上画两条平行线AB、CD,再画直线MN与直线AB,CD相交(如下图)
任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?由此你能得到什么结论?
3
4
1
5
2
6
8
7
导入新课
情境引入
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
情境导入
想一想:
生活中的问题能用数学知识解决吗?
a
b
c
如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线 a和b平行
③直线a和b不平行
做一做
●
一、放
二、靠
三、推
四、画
用三角尺和直尺画平行线的方法.
利用同位角判定两条直线平行
讲授新课
●
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线a,b位置关系如何?
问题
(4)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的
方法吗?
判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2 (同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
练习:下图中若∠1=550 ,∠2=550,直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
同位角相等,两直线平行.
变式1:
如图, ∠1=55 , ∠2=125 ,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
同位角相等,两直线平行.
变式2:
如图, 直线AB与CD被直线EF所截,∠1=55 ,请添加一个条件使得直线AB与直线CD平行.
A
C
E
F
B
D
1
3
2
5
4
∠5=55
你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?
练一练
例1 如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解析:根据AB∥DC及∠D=125°,可求出∠A的度数,从而说明∠A=∠CBE.再根据同位角相等,两直线平行可得AD∥BC.
B
A
D
C
E
解:AD∥BC.
理由如下:因为AB∥DC(已知),
所以∠A+∠D=180°(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D=180°-125°=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE,所以AD∥BC
(同位角相等,两直线平行).
1.从∠5=∠ ,可以推出AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
当堂练习
2.如图所示,已知直线EF和AB,CD分别
相交于K,H,且∠EGB=90°,∠CHF=60°,
∠E=30°,试说明AB∥CD.
解:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
由同位角的关系判断两直线平行的三个步骤:
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.
课堂小结
见对应习题。
课后作业
