人教版数学三年级下册 第5单元第2节《长方形、正方形面积的计算》教案
文档属性
| 名称 | 人教版数学三年级下册 第5单元第2节《长方形、正方形面积的计算》教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 604.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览




文档简介
2长方形、正方形面积的计算
备教材内容
1.本课时学习的是教材66~67页的内容。
2.本课时教学长方形、正方形面积计算的相关知识。在探究例4的过程中,学生经历了“动手实践,初步感知是什么——深入探究,理解为什么——沟通联系,形成认知结构”的全过程,从而激发学生的探究欲望,培养学生的探究能力。例5是对长方形面积计算公式的简单应用,既可以提高学生用长方形面积计算公式解决实际问题的能力,又可以通过计算知道这些常见物体的面积是多少,丰富学生的感性经验,为以后估计其他物体的面积提供参考依据。
3.本课时是学习基础图形面积的计算,是进一步学习其他图形面积计算的基础。
备已学知识
1.长度单位:千米、米、分米、厘米、毫米。
2.长方形的周长:(长+宽)×2。
3.正方形的周长:边长×4。
4.常用的面积单位:平方厘米、平方分米、平方米。
备教学目标
知识与技能
1.理解长方形、正方形面积计算公式的意义,掌握长方形和正方形的面积计算公式。
2.能用长方形、正方形的面积计算公式进行计算,并能解决简单的实际问题。
过程与方法
1.在实践操作中,经历长方形、正方形面积计算公式的推导过程,获得从度量到计算来研究长方形、正方形面积的方法。
2.通过猜想、分析、推理得出长方形、正方形的面积计算公式,培养学生的推理能力。
情感、态度与价值观
1.在解决问题的过程中,形成关于面积单位实际大小的正确表象。
2.通过实践操作,体验动手实践的快乐及探究分析的乐趣。
备重点难点
重点:理解并掌握长方形、正方形面积的计算公式及应用公式解决实际问题。
难点:理解长方形面积计算公式的意义。
备知识讲解
知识点一 长方形的面积计算公式
问题导入 一个长方形长5厘米、宽3厘米。你能求出它的面积吗?[教材66页例4(1)]
过程讲解
1.观图、读题,理解题意
已知长方形的长和宽,要求求出这个长方形的面积。
2.探究计量长方形面积的方法
难点点拨 求长方形的面积就是求它含有多少个面积单位。
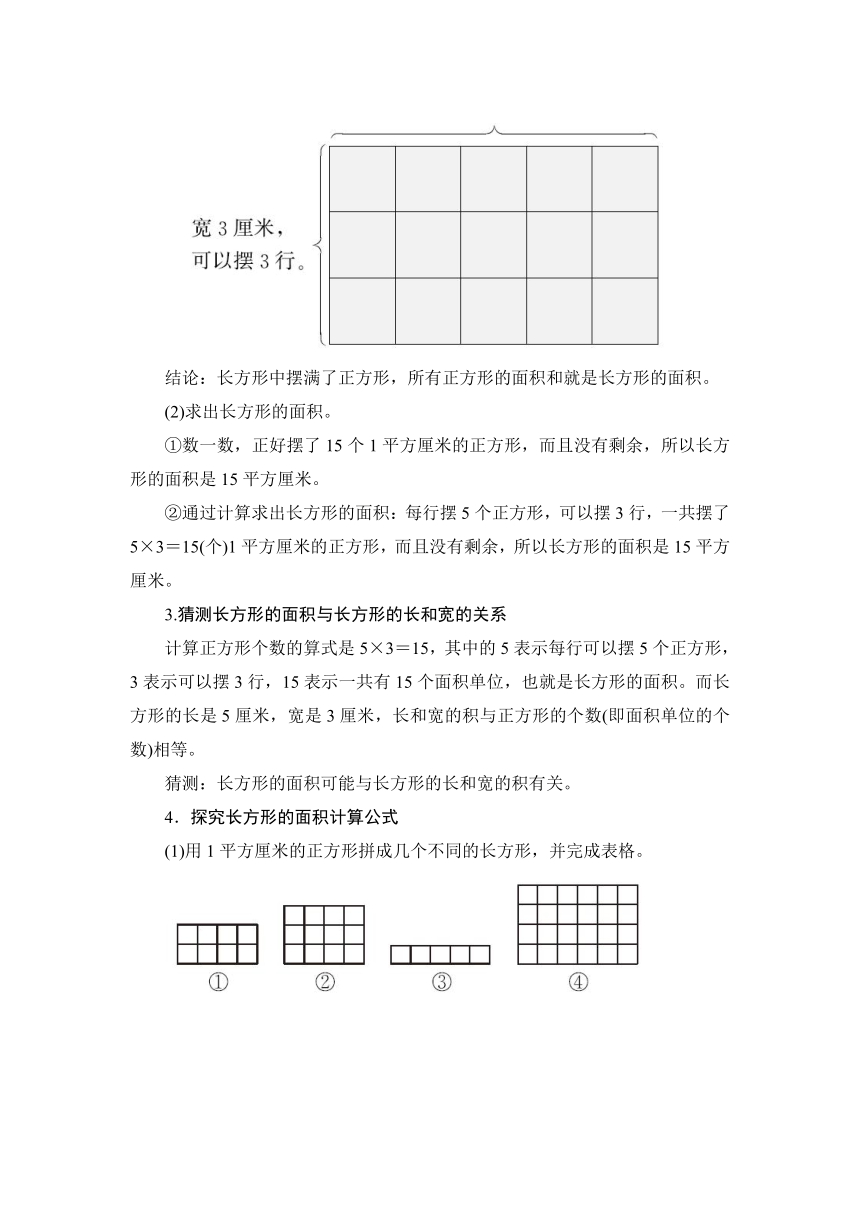
(1)实际摆一摆,借助面积是1平方厘米的正方形来计量长方形的面积。
在长方形中摆面积是1平方厘米的正方形,如下图:
长5厘米,每行可以摆5个1平方厘米的正方形。
结论:长方形中摆满了正方形,所有正方形的面积和就是长方形的面积。
(2)求出长方形的面积。
①数一数,正好摆了15个1平方厘米的正方形,而且没有剩余,所以长方形的面积是15平方厘米。
②通过计算求出长方形的面积:每行摆5个正方形,可以摆3行,一共摆了5×3=15(个)1平方厘米的正方形,而且没有剩余,所以长方形的面积是15平方厘米。
3.猜测长方形的面积与长方形的长和宽的关系
计算正方形个数的算式是5×3=15,其中的5表示每行可以摆5个正方形,3表示可以摆3行,15表示一共有15个面积单位,也就是长方形的面积。而长方形的长是5厘米,宽是3厘米,长和宽的积与正方形的个数(即面积单位的个数)相等。
猜测:长方形的面积可能与长方形的长和宽的积有关。
4.探究长方形的面积计算公式
(1)用1平方厘米的正方形拼成几个不同的长方形,并完成表格。
图形 ① ② ③ ④
每行个数(长/厘米) 4 4 5 6
行数(宽/厘米) 2 3 1 4
正方形的个数 4×2=8 4×3=12 5×1=5 6×4=24
面积/平方厘米 8 12 5 24
(2)分析数据。
长方形的面积 长方形的长 长方形的宽
8 = 4 × 2
12 = 4 × 3
5 = 5 × 1
24 = 6 × 4
(3)推导长方形的面积计算公式。
长方形的面积=长×宽
5.运用长方形的面积计算公式解决问题
5×3=15(平方厘米)
答:它的面积是15平方厘米。
归纳总结
长方形的面积计算公式:长方形的面积=长×宽。
知识点二 正方形的面积计算公式
问题导入 先量一量,再计算它们的面积。[教材66页例4(3)]
长=______ 长=______
宽=______ 宽=______
面积=______ 面积=______
过程讲解
1.读题,理解题意
给出两个图形,图形的长和宽未知,要求求出这两个图形的面积。
2.明确解题思路
要求这两个图形的面积,应先测量出这两个图形的长和宽,再运用图形的面积计算公式进行计算。
3.实际操作,测量长度
第一个图形的长是5厘米,宽是2厘米,它是长方形;第二个图形的长和宽都是3厘米,它是正方形。
4.运用长方形的面积计算公式计算长方形的面积
5×2=10(平方厘米)
5.推导正方形的面积计算公式
(1)明确长方形和正方形的关系:当长方形的长和宽相等时,这个长方形就是正方形,此时长和宽统称为边长,因此,正方形是特殊的长方形。
(2)根据长方形的面积计算公式推导出正方形的面积计算公式。
长方形的面积= 长 × 宽
正方形的面积=边长×边长
[思想方法提示:根据长方形的面积计算公式推导出正方形的面积计算公式,体现了类比的思想方法。]
6.运用正方形的面积计算公式计算正方形的面积
3×3=9(平方厘米)
归纳总结
正方形的面积计算公式:正方形的面积=边长×边长。
知识点三 运用长方形、正方形的面积计算公式解决问题
问题导入 数学书封面的长大约是26厘米,宽大约是18厘米。数学书封面的面积大约是多少平方厘米?利用数学书封面的面积,估计一下你的课桌面的面积。(教材67页例5)
过程讲解
1.读题,明确解题思路
先计算出数学书封面的面积,再利用数学书封面的面积估计课桌面的面积。
2.计算数学书封面的面积
(1)解题方法:数学书封面是长方形,已知长方形的长和宽,可以运用长方形的面积计算公式直接计算。
(2)解题过程:26×18=468(平方厘米)
答:数学书封面的面积大约是468平方厘米。
3.利用数学书封面的面积估计课桌面的面积
(1)估计方法:利用数学书封面的面积估计课桌面的面积,也就是估计课桌面有几个数学书封面那么大。可以目测几本数学书能铺满课桌面,也可以将数学书放在课桌面上比一比。
(2)估计结果:课桌面的面积大约有5个数学书封面的面积那么大。
归纳总结
1.已知长方形的长和宽,可以运用长方形的面积计算公式求出长方形的面积。
2.估计物品的面积,可以借助熟悉的物品面积作为“非标准”面积单位,也可以根据已有经验进行估计。
备易错易混
误区一 一个正方形花坛的周长是12米,这个花坛的面积是多少平方米?
12×12=144(平方米)
答:这个花坛的面积是144平方米。
错解分析 此题错在把周长12米认为是正方形的边长。应先根据“边长=周长÷4”求出正方形的边长,再根据正方形的面积计算公式求出面积。
错解改正 12÷4=3(米) 3×3=9(平方米)
答:这个花坛的面积是9平方米。
温馨提示
已知正方形的周长,求面积,应先用“周长÷4”求出边长,再用“边长×边长”求出面积。
误区二 一个长方形长3米、宽10分米,这个长方形的面积是多少平方分米?
3×10=30(平方分米)
答:这个长方形的面积是30平方分米。
错解分析 此题错在没有统一单位就直接计算了。
错解改正 3米=30分米
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
温馨提示
计算面积时,要先统一单位,再运用面积计算公式进行计算。
备综合能力
方法运用 运用图示法解决求正方形面积的问题
典型例题 一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
思路分析 根据题意,把边长增加后的新正方形分成四部分。如下图:
从上图中可以看出,增加的部分是①、②、③,其中①和②的宽都是3厘米,它们是两个完全相同的长方形,而③是边长为3厘米的小正方形。由此可以推出:
根据正方形的面积计算公式可以求出原正方形的面积。
正确解答 39-3×3=30(平方厘米)
30÷2=15(平方厘米) 15÷3=5(厘米)
5×5=25(平方厘米)
答:原正方形的面积是25平方厘米。
方法总结 已知长方形的面积计算公式中的任意两个量,都可以求出第三个量,即长方形的面积=长×宽;长方形的长=面积÷宽;长方形的宽=面积÷长。
思维开放 运用观察法和转化法解决面积问题
典型例题 下图是用6个相同的小长方形拼成的。1个小长方形的面积是多少平方分米?
思路分析 整个图形是一个大长方形,可先找出大长方形与小长方形之间的数量关系,再进行转化推理。
大长方形的宽=小长方形的长=小长方形宽的5倍
大长方形的长=小长方形的长+小长方形的宽
由此可推得:
大长方形的长=小长方形宽的6倍
已知大长方形的长=42分米,可求出小长方形的宽,从而求出小长方形的长,进而求出小长方形的面积。
正确解答 42÷(5+1)=7(分米)
7×5=35(分米) 35×7=245(平方分米)
答:1个小长方形的面积是245平方分米。
方法提示 明确图形之间的关系是解决此类问题的关键。
备教学资料
巧移火柴
如下图所示的方格图案由28根火柴组成,共有5个正方形。
把一根火柴的长度作为单位长度,那么图中5个正方形的总面积是4×2+1×3=11。用28根火柴,还是组成5个正方形,但是要使总面积变大,能不能做到呢?
正确解答 (摆法不唯一)
边长为1的正方形有4个,边长为4的正方形有1个,它们的面积和是1×4+16×1=20。
生活趣味数学题:失踪的正方形
在一张正方形纸板上按图1所示画上7×7=49(个)小正方形,然后沿图示剪成5个小块纸板。当你按图2所示将这5个小块纸板重新拼起来的时候,你会发现不可思议的事情发生了:中间居然出现了一个方洞!图1是由49个小正方形组成的。图2却只有48个小正方形。哪个小正方形没有了?它到哪儿去了?
正确解答 原来5个小块纸板中最大的两块2和3对换位置以后,2和3的面积和原来都不相等了,都比原来少了,少的面积和就是这个方洞的面积。
备教材内容
1.本课时学习的是教材66~67页的内容。
2.本课时教学长方形、正方形面积计算的相关知识。在探究例4的过程中,学生经历了“动手实践,初步感知是什么——深入探究,理解为什么——沟通联系,形成认知结构”的全过程,从而激发学生的探究欲望,培养学生的探究能力。例5是对长方形面积计算公式的简单应用,既可以提高学生用长方形面积计算公式解决实际问题的能力,又可以通过计算知道这些常见物体的面积是多少,丰富学生的感性经验,为以后估计其他物体的面积提供参考依据。
3.本课时是学习基础图形面积的计算,是进一步学习其他图形面积计算的基础。
备已学知识
1.长度单位:千米、米、分米、厘米、毫米。
2.长方形的周长:(长+宽)×2。
3.正方形的周长:边长×4。
4.常用的面积单位:平方厘米、平方分米、平方米。
备教学目标
知识与技能
1.理解长方形、正方形面积计算公式的意义,掌握长方形和正方形的面积计算公式。
2.能用长方形、正方形的面积计算公式进行计算,并能解决简单的实际问题。
过程与方法
1.在实践操作中,经历长方形、正方形面积计算公式的推导过程,获得从度量到计算来研究长方形、正方形面积的方法。
2.通过猜想、分析、推理得出长方形、正方形的面积计算公式,培养学生的推理能力。
情感、态度与价值观
1.在解决问题的过程中,形成关于面积单位实际大小的正确表象。
2.通过实践操作,体验动手实践的快乐及探究分析的乐趣。
备重点难点
重点:理解并掌握长方形、正方形面积的计算公式及应用公式解决实际问题。
难点:理解长方形面积计算公式的意义。
备知识讲解
知识点一 长方形的面积计算公式
问题导入 一个长方形长5厘米、宽3厘米。你能求出它的面积吗?[教材66页例4(1)]
过程讲解
1.观图、读题,理解题意
已知长方形的长和宽,要求求出这个长方形的面积。
2.探究计量长方形面积的方法
难点点拨 求长方形的面积就是求它含有多少个面积单位。
(1)实际摆一摆,借助面积是1平方厘米的正方形来计量长方形的面积。
在长方形中摆面积是1平方厘米的正方形,如下图:
长5厘米,每行可以摆5个1平方厘米的正方形。
结论:长方形中摆满了正方形,所有正方形的面积和就是长方形的面积。
(2)求出长方形的面积。
①数一数,正好摆了15个1平方厘米的正方形,而且没有剩余,所以长方形的面积是15平方厘米。
②通过计算求出长方形的面积:每行摆5个正方形,可以摆3行,一共摆了5×3=15(个)1平方厘米的正方形,而且没有剩余,所以长方形的面积是15平方厘米。
3.猜测长方形的面积与长方形的长和宽的关系
计算正方形个数的算式是5×3=15,其中的5表示每行可以摆5个正方形,3表示可以摆3行,15表示一共有15个面积单位,也就是长方形的面积。而长方形的长是5厘米,宽是3厘米,长和宽的积与正方形的个数(即面积单位的个数)相等。
猜测:长方形的面积可能与长方形的长和宽的积有关。
4.探究长方形的面积计算公式
(1)用1平方厘米的正方形拼成几个不同的长方形,并完成表格。
图形 ① ② ③ ④
每行个数(长/厘米) 4 4 5 6
行数(宽/厘米) 2 3 1 4
正方形的个数 4×2=8 4×3=12 5×1=5 6×4=24
面积/平方厘米 8 12 5 24
(2)分析数据。
长方形的面积 长方形的长 长方形的宽
8 = 4 × 2
12 = 4 × 3
5 = 5 × 1
24 = 6 × 4
(3)推导长方形的面积计算公式。
长方形的面积=长×宽
5.运用长方形的面积计算公式解决问题
5×3=15(平方厘米)
答:它的面积是15平方厘米。
归纳总结
长方形的面积计算公式:长方形的面积=长×宽。
知识点二 正方形的面积计算公式
问题导入 先量一量,再计算它们的面积。[教材66页例4(3)]
长=______ 长=______
宽=______ 宽=______
面积=______ 面积=______
过程讲解
1.读题,理解题意
给出两个图形,图形的长和宽未知,要求求出这两个图形的面积。
2.明确解题思路
要求这两个图形的面积,应先测量出这两个图形的长和宽,再运用图形的面积计算公式进行计算。
3.实际操作,测量长度
第一个图形的长是5厘米,宽是2厘米,它是长方形;第二个图形的长和宽都是3厘米,它是正方形。
4.运用长方形的面积计算公式计算长方形的面积
5×2=10(平方厘米)
5.推导正方形的面积计算公式
(1)明确长方形和正方形的关系:当长方形的长和宽相等时,这个长方形就是正方形,此时长和宽统称为边长,因此,正方形是特殊的长方形。
(2)根据长方形的面积计算公式推导出正方形的面积计算公式。
长方形的面积= 长 × 宽
正方形的面积=边长×边长
[思想方法提示:根据长方形的面积计算公式推导出正方形的面积计算公式,体现了类比的思想方法。]
6.运用正方形的面积计算公式计算正方形的面积
3×3=9(平方厘米)
归纳总结
正方形的面积计算公式:正方形的面积=边长×边长。
知识点三 运用长方形、正方形的面积计算公式解决问题
问题导入 数学书封面的长大约是26厘米,宽大约是18厘米。数学书封面的面积大约是多少平方厘米?利用数学书封面的面积,估计一下你的课桌面的面积。(教材67页例5)
过程讲解
1.读题,明确解题思路
先计算出数学书封面的面积,再利用数学书封面的面积估计课桌面的面积。
2.计算数学书封面的面积
(1)解题方法:数学书封面是长方形,已知长方形的长和宽,可以运用长方形的面积计算公式直接计算。
(2)解题过程:26×18=468(平方厘米)
答:数学书封面的面积大约是468平方厘米。
3.利用数学书封面的面积估计课桌面的面积
(1)估计方法:利用数学书封面的面积估计课桌面的面积,也就是估计课桌面有几个数学书封面那么大。可以目测几本数学书能铺满课桌面,也可以将数学书放在课桌面上比一比。
(2)估计结果:课桌面的面积大约有5个数学书封面的面积那么大。
归纳总结
1.已知长方形的长和宽,可以运用长方形的面积计算公式求出长方形的面积。
2.估计物品的面积,可以借助熟悉的物品面积作为“非标准”面积单位,也可以根据已有经验进行估计。
备易错易混
误区一 一个正方形花坛的周长是12米,这个花坛的面积是多少平方米?
12×12=144(平方米)
答:这个花坛的面积是144平方米。
错解分析 此题错在把周长12米认为是正方形的边长。应先根据“边长=周长÷4”求出正方形的边长,再根据正方形的面积计算公式求出面积。
错解改正 12÷4=3(米) 3×3=9(平方米)
答:这个花坛的面积是9平方米。
温馨提示
已知正方形的周长,求面积,应先用“周长÷4”求出边长,再用“边长×边长”求出面积。
误区二 一个长方形长3米、宽10分米,这个长方形的面积是多少平方分米?
3×10=30(平方分米)
答:这个长方形的面积是30平方分米。
错解分析 此题错在没有统一单位就直接计算了。
错解改正 3米=30分米
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
温馨提示
计算面积时,要先统一单位,再运用面积计算公式进行计算。
备综合能力
方法运用 运用图示法解决求正方形面积的问题
典型例题 一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
思路分析 根据题意,把边长增加后的新正方形分成四部分。如下图:
从上图中可以看出,增加的部分是①、②、③,其中①和②的宽都是3厘米,它们是两个完全相同的长方形,而③是边长为3厘米的小正方形。由此可以推出:
根据正方形的面积计算公式可以求出原正方形的面积。
正确解答 39-3×3=30(平方厘米)
30÷2=15(平方厘米) 15÷3=5(厘米)
5×5=25(平方厘米)
答:原正方形的面积是25平方厘米。
方法总结 已知长方形的面积计算公式中的任意两个量,都可以求出第三个量,即长方形的面积=长×宽;长方形的长=面积÷宽;长方形的宽=面积÷长。
思维开放 运用观察法和转化法解决面积问题
典型例题 下图是用6个相同的小长方形拼成的。1个小长方形的面积是多少平方分米?
思路分析 整个图形是一个大长方形,可先找出大长方形与小长方形之间的数量关系,再进行转化推理。
大长方形的宽=小长方形的长=小长方形宽的5倍
大长方形的长=小长方形的长+小长方形的宽
由此可推得:
大长方形的长=小长方形宽的6倍
已知大长方形的长=42分米,可求出小长方形的宽,从而求出小长方形的长,进而求出小长方形的面积。
正确解答 42÷(5+1)=7(分米)
7×5=35(分米) 35×7=245(平方分米)
答:1个小长方形的面积是245平方分米。
方法提示 明确图形之间的关系是解决此类问题的关键。
备教学资料
巧移火柴
如下图所示的方格图案由28根火柴组成,共有5个正方形。
把一根火柴的长度作为单位长度,那么图中5个正方形的总面积是4×2+1×3=11。用28根火柴,还是组成5个正方形,但是要使总面积变大,能不能做到呢?
正确解答 (摆法不唯一)
边长为1的正方形有4个,边长为4的正方形有1个,它们的面积和是1×4+16×1=20。
生活趣味数学题:失踪的正方形
在一张正方形纸板上按图1所示画上7×7=49(个)小正方形,然后沿图示剪成5个小块纸板。当你按图2所示将这5个小块纸板重新拼起来的时候,你会发现不可思议的事情发生了:中间居然出现了一个方洞!图1是由49个小正方形组成的。图2却只有48个小正方形。哪个小正方形没有了?它到哪儿去了?
正确解答 原来5个小块纸板中最大的两块2和3对换位置以后,2和3的面积和原来都不相等了,都比原来少了,少的面积和就是这个方洞的面积。
