北师大版数学九年级上册同步课时练习:第5章 投影与视图 单元复习小结 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:第5章 投影与视图 单元复习小结 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 16:36:05 | ||
图片预览

文档简介
单元复习小结
类型之一 中心投影与平行投影
1.如图下列判断正确的是 ( )
A.图①是在阳光下的影子,图②是在灯光下的影子
B.图②是在阳光下的影子,图①是在灯光下的影子
C.图①和图②都是在阳光下的影子
D.图①和图②都是在灯光下的影子
2.圆形的物体在太阳光下的投影是 ( )
A.圆形 B.椭圆形 C.线段 D.以上都有可能
3.如图图甲、图乙分别是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形 哪个图反映了路灯下的情形 判断它们是平行投影还是中心投影,并说明理由;
(2)请画出两图中表示小明影长的线段;
(3)阳光下小明的影长为1.20 m,树的影长为2.40 m,小明的身高为1.88 m,求树高.
类型之二 几何体的三视图
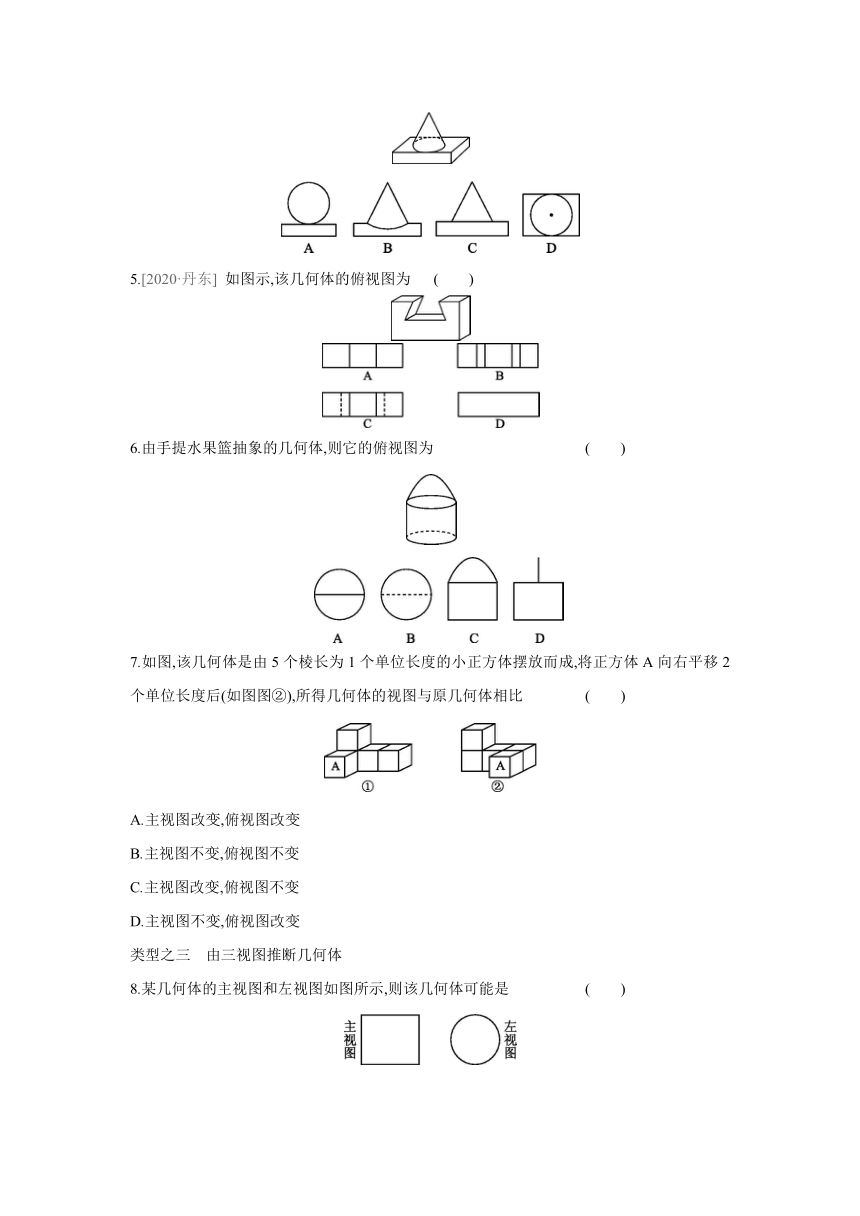
4.[2020·辽阳] 由一个长方体和一个圆锥组成的几何体,它的主视图是 ( )
5.[2020·丹东] 如图示,该几何体的俯视图为 ( )
6.由手提水果篮抽象的几何体,则它的俯视图为 ( )
7.如图,该几何体是由5个棱长为1个单位长度的小正方体摆放而成,将正方体A向右平移2个单位长度后(如图图②),所得几何体的视图与原几何体相比 ( )
A.主视图改变,俯视图改变
B.主视图不变,俯视图不变
C.主视图改变,俯视图不变
D.主视图不变,俯视图改变
类型之三 由三视图推断几何体
8.某几何体的主视图和左视图如图所示,则该几何体可能是 ( )
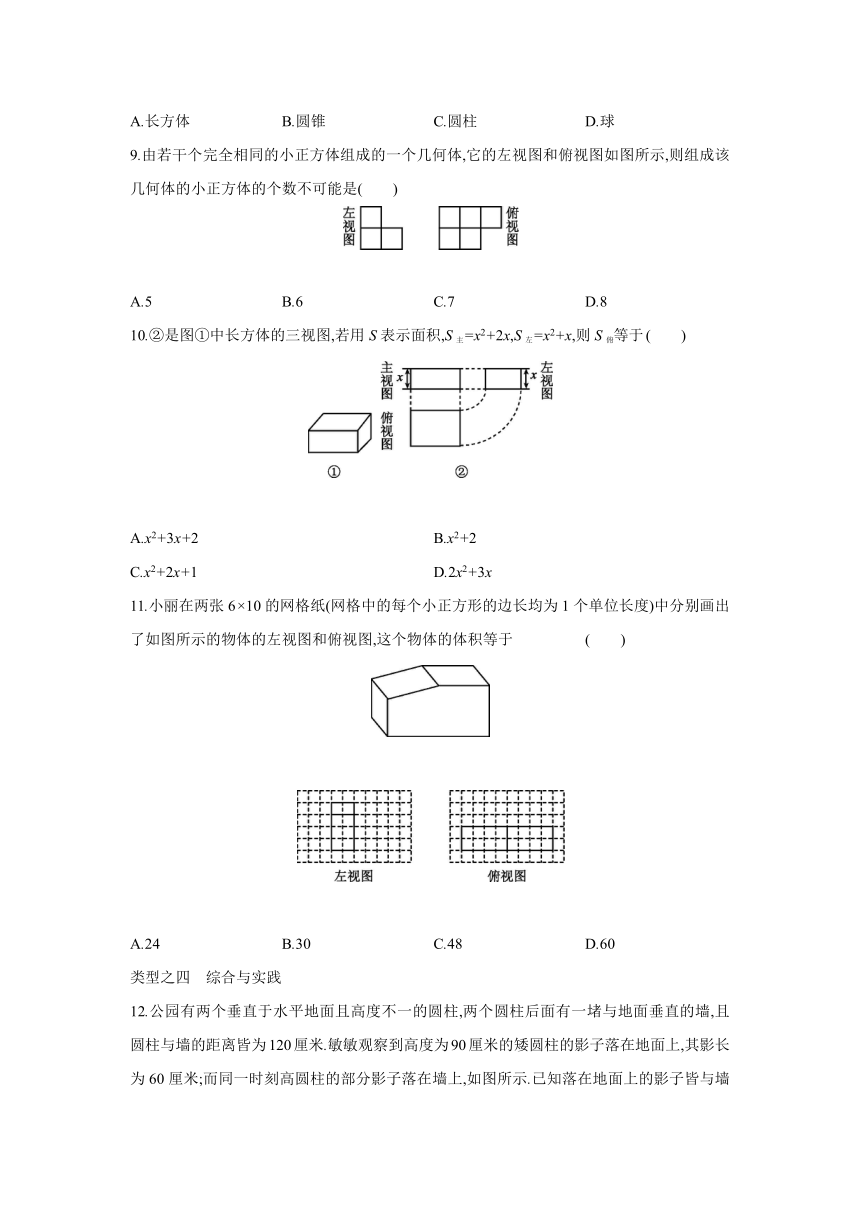
A.长方体 B.圆锥 C.圆柱 D.球
9.由若干个完全相同的小正方体组成的一个几何体,它的左视图和俯视图如图所示,则组成该几何体的小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
10.②是图①中长方体的三视图,若用S表示面积,S主=x2+2x,S左=x2+x,则S俯等于 ( )
A.x2+3x+2 B.x2+2
C.x2+2x+1 D.2x2+3x
11.小丽在两张6×10的网格纸(网格中的每个小正方形的边长均为1个单位长度)中分别画出了如图所示的物体的左视图和俯视图,这个物体的体积等于 ( )
A.24 B.30 C.48 D.60
类型之四 综合与实践
12.公园有两个垂直于水平地面且高度不一的圆柱,两个圆柱后面有一堵与地面垂直的墙,且圆柱与墙的距离皆为120厘米.敏敏观察到高度为90厘米的矮圆柱的影子落在地面上,其影长为60厘米;而同一时刻高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相垂直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为150厘米,且此刻她的影子完全落在地面上,则她的影长为多少厘米
(2)若同一时间量得高圆柱落在墙上的影长为150厘米,则高圆柱的高度为多少厘米
答案
1.B
2.D
3.解:(1)如图图所示.
图甲反映了阳光下的情形,图乙反映了路灯下的情形.
图甲是平行投影,因为它们的投影线是平行的.
图乙是中心投影,因为它们的投影线是相交的.
(2)如图图所示,AB,CD分别是表示小明影长的线段.
(3)设树高为x m.
∵阳光下小明的影长为1.20 m,树的影长为2.40 m,小明的身高为1.88 m,
∴=,
解得x=3.76.
答:树高为3.76 m.
4.C 5.C
6.A 7.D 8.C
9.A 由左视图可知,从下往上数第二层上至少有1个小正方体,第一层一共有5个小正方体,故小正方体的个数最少为6,则小正方体的个数不可能是5.故选A.
10.A ∵S主=x2+2x=x(x+2),S左=x2+x=x(x+1),
∴俯视图的长为x+2,宽为x+1,
则俯视图的面积S俯=(x+2)(x+1)=x2+3x+2.故选A.
11.D
12.解:(1)设敏敏的影长为x厘米.
由题意,得=,解得x=100.
∴敏敏的影长为100厘米.
(2)如图图,连接AE,作FB∥AE交AC于点B.
又∵AB∥EF,∴四边形ABFE是平行四边形,
∴AB=EF=150厘米.
设BC=y厘米,由题意知BC落在地面上的影长为120厘米,
则=,解得y=180,
∴AC=AB+BC=150+180=330(厘米).
即高圆柱的高度为330厘米.
类型之一 中心投影与平行投影
1.如图下列判断正确的是 ( )
A.图①是在阳光下的影子,图②是在灯光下的影子
B.图②是在阳光下的影子,图①是在灯光下的影子
C.图①和图②都是在阳光下的影子
D.图①和图②都是在灯光下的影子
2.圆形的物体在太阳光下的投影是 ( )
A.圆形 B.椭圆形 C.线段 D.以上都有可能
3.如图图甲、图乙分别是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形 哪个图反映了路灯下的情形 判断它们是平行投影还是中心投影,并说明理由;
(2)请画出两图中表示小明影长的线段;
(3)阳光下小明的影长为1.20 m,树的影长为2.40 m,小明的身高为1.88 m,求树高.
类型之二 几何体的三视图
4.[2020·辽阳] 由一个长方体和一个圆锥组成的几何体,它的主视图是 ( )
5.[2020·丹东] 如图示,该几何体的俯视图为 ( )
6.由手提水果篮抽象的几何体,则它的俯视图为 ( )
7.如图,该几何体是由5个棱长为1个单位长度的小正方体摆放而成,将正方体A向右平移2个单位长度后(如图图②),所得几何体的视图与原几何体相比 ( )
A.主视图改变,俯视图改变
B.主视图不变,俯视图不变
C.主视图改变,俯视图不变
D.主视图不变,俯视图改变
类型之三 由三视图推断几何体
8.某几何体的主视图和左视图如图所示,则该几何体可能是 ( )
A.长方体 B.圆锥 C.圆柱 D.球
9.由若干个完全相同的小正方体组成的一个几何体,它的左视图和俯视图如图所示,则组成该几何体的小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
10.②是图①中长方体的三视图,若用S表示面积,S主=x2+2x,S左=x2+x,则S俯等于 ( )
A.x2+3x+2 B.x2+2
C.x2+2x+1 D.2x2+3x
11.小丽在两张6×10的网格纸(网格中的每个小正方形的边长均为1个单位长度)中分别画出了如图所示的物体的左视图和俯视图,这个物体的体积等于 ( )
A.24 B.30 C.48 D.60
类型之四 综合与实践
12.公园有两个垂直于水平地面且高度不一的圆柱,两个圆柱后面有一堵与地面垂直的墙,且圆柱与墙的距离皆为120厘米.敏敏观察到高度为90厘米的矮圆柱的影子落在地面上,其影长为60厘米;而同一时刻高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相垂直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为150厘米,且此刻她的影子完全落在地面上,则她的影长为多少厘米
(2)若同一时间量得高圆柱落在墙上的影长为150厘米,则高圆柱的高度为多少厘米
答案
1.B
2.D
3.解:(1)如图图所示.
图甲反映了阳光下的情形,图乙反映了路灯下的情形.
图甲是平行投影,因为它们的投影线是平行的.
图乙是中心投影,因为它们的投影线是相交的.
(2)如图图所示,AB,CD分别是表示小明影长的线段.
(3)设树高为x m.
∵阳光下小明的影长为1.20 m,树的影长为2.40 m,小明的身高为1.88 m,
∴=,
解得x=3.76.
答:树高为3.76 m.
4.C 5.C
6.A 7.D 8.C
9.A 由左视图可知,从下往上数第二层上至少有1个小正方体,第一层一共有5个小正方体,故小正方体的个数最少为6,则小正方体的个数不可能是5.故选A.
10.A ∵S主=x2+2x=x(x+2),S左=x2+x=x(x+1),
∴俯视图的长为x+2,宽为x+1,
则俯视图的面积S俯=(x+2)(x+1)=x2+3x+2.故选A.
11.D
12.解:(1)设敏敏的影长为x厘米.
由题意,得=,解得x=100.
∴敏敏的影长为100厘米.
(2)如图图,连接AE,作FB∥AE交AC于点B.
又∵AB∥EF,∴四边形ABFE是平行四边形,
∴AB=EF=150厘米.
设BC=y厘米,由题意知BC落在地面上的影长为120厘米,
则=,解得y=180,
∴AC=AB+BC=150+180=330(厘米).
即高圆柱的高度为330厘米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
