北师大版数学九年级上册同步课时练习:第6章 反比例函数 单元复习小结 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:第6章 反比例函数 单元复习小结 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 17:49:36 | ||
图片预览


文档简介
单元复习小结
类型之一 反比例函数的概念
1.若y=(a+1)是关于x的反比例函数,则a的取值为 ( )
A.1 B.-1 C.±1 D.任意实数
2.已知点A与点B关于原点对称,点A的坐标是(2,-3),那么图象经过点B的反比例函数的表达式是 ( )
A.y=- B.y=- C.y=- D.y=-
3.今年,某公司推出一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 (不用体现自变量的取值范围).
类型之二 反比例函数的图象和性质
4.[2020·衡阳] 反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.函数的图形既是轴对称图形,又是中心对称图形
5.如图果反比例函数y=(a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C.a<2 D.a>2
6.已知点A(2,y1),B(4,y2)都在反比例函数y=(k<0)的图象上,则y1,y2的大小关系为 ( )
A.y1>y2 B.y17.如图边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=-的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是 ( )
A.4 B.6 C.8 D.10
8.如图A,B是函数y=(x>0)的图象上的两点,过点A作AC⊥x轴,交OB于点D,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为 ( )
A. B. C.3 D.4
9.[2020·烟台] 如图正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是 ( )
A.x<-1 B.-0.51 C.010.如图直线y=k1x+b与反比例函数y=在第二象限内的图象相交于点A,B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的表达式;
(2)求△AOC的面积.
类型之三 反比例函数的应用
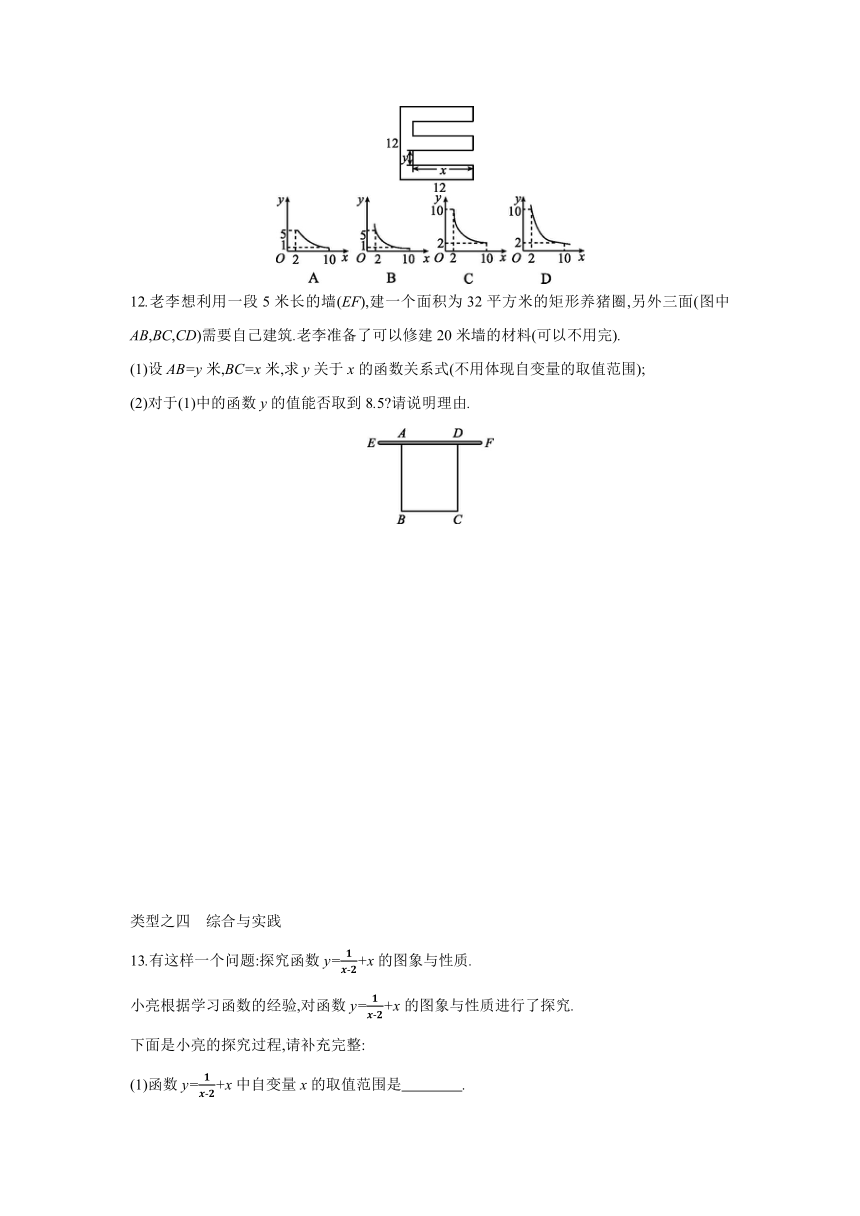
11.一张正方形纸片,剪去两个一样的小矩形得到一个“E”图案,如图示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是 ( )
12.老李想利用一段5米长的墙(EF),建一个面积为32平方米的矩形养猪圈,另外三面(图中AB,BC,CD)需要自己建筑.老李准备了可以修建20米墙的材料(可以不用完).
(1)设AB=y米,BC=x米,求y关于x的函数关系式(不用体现自变量的取值范围);
(2)对于(1)中的函数y的值能否取到8.5 请说明理由.
类型之四 综合与实践
13.有这样一个问题:探究函数y=+x的图象与性质.
小亮根据学习函数的经验,对函数y=+x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y=+x中自变量x的取值范围是 .
(2)下表是y与x的几组对应值,请直接写出m的值: .
x … -2 -1 0 1 3 4 5 6 …
y … - - - 0 - - m …
(3)在如图示的平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象.
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与直线x=2越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.
答案
1.A
2.C ∵点A(2,-3),点A与点B关于原点对称,∴点B的坐标为(-2,3).∵反比例函数的图象经过点B,∴反比例函数的表达式是y=-.
3.y= 由题意,得y=,即y=.
4.C
5.D ∵反比例函数的图象在第一、三象限,∴a-2>0,∴a>2.故选D.
6.B 7.C
8.B 如图图,过点B作BE⊥x轴于点E.
∵AC⊥x轴,
∴AC∥BE,
可得△OCD∽△OEB,
∴==.
∵D为OB的中点,
∴OD=OB,
∴OC=OE,CD=BE.
设A,则B,CD=,
∴AD=-.
∵△ADO的面积为1.
∴AD·OC=1,
即·x=1,
解得k=.故选B.
9.D
10.解:(1)∵点A(-2,4)在反比例函数y=的图象上,
∴k2=-8.
∴反比例函数的表达式为y=-.
(2)∵点B的横坐标为-4,
∴其纵坐标为2,
∴B(-4,2).
∵点A(-2,4),B(-4,2)在直线y=k1x+b上,
∴ 解得
∴直线AB的函数表达式为y=x+6,它与x轴的交点C的坐标为(-6,0),
∴S△AOC=×6×4=12.
11.A ∵剪去两个一样的小矩形,两个矩形的面积和为20,∴xy=10,∴y是x的反比例函数.∵2≤x≤10,∴答案为A.
12.解:(1)依题意,得xy=32,∴y=.
(2)不能.理由:当y=8.5时,=8.5,
∴x=,∴x+2y=20.
∵20>20,∴对于(1)中的函数y的值不能取到8.5.
13.解:(1)由题意得x-2≠0,解得x≠2.故答案为x≠2.
(2)当x=3时,m=+3=1+3=4.故答案为4.
(3)图象如图图所示.
(4)①(2,2) ②y=x
类型之一 反比例函数的概念
1.若y=(a+1)是关于x的反比例函数,则a的取值为 ( )
A.1 B.-1 C.±1 D.任意实数
2.已知点A与点B关于原点对称,点A的坐标是(2,-3),那么图象经过点B的反比例函数的表达式是 ( )
A.y=- B.y=- C.y=- D.y=-
3.今年,某公司推出一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 (不用体现自变量的取值范围).
类型之二 反比例函数的图象和性质
4.[2020·衡阳] 反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.函数的图形既是轴对称图形,又是中心对称图形
5.如图果反比例函数y=(a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C.a<2 D.a>2
6.已知点A(2,y1),B(4,y2)都在反比例函数y=(k<0)的图象上,则y1,y2的大小关系为 ( )
A.y1>y2 B.y1
A.4 B.6 C.8 D.10
8.如图A,B是函数y=(x>0)的图象上的两点,过点A作AC⊥x轴,交OB于点D,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为 ( )
A. B. C.3 D.4
9.[2020·烟台] 如图正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是 ( )
A.x<-1 B.-0.5
(1)试确定反比例函数的表达式;
(2)求△AOC的面积.
类型之三 反比例函数的应用
11.一张正方形纸片,剪去两个一样的小矩形得到一个“E”图案,如图示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是 ( )
12.老李想利用一段5米长的墙(EF),建一个面积为32平方米的矩形养猪圈,另外三面(图中AB,BC,CD)需要自己建筑.老李准备了可以修建20米墙的材料(可以不用完).
(1)设AB=y米,BC=x米,求y关于x的函数关系式(不用体现自变量的取值范围);
(2)对于(1)中的函数y的值能否取到8.5 请说明理由.
类型之四 综合与实践
13.有这样一个问题:探究函数y=+x的图象与性质.
小亮根据学习函数的经验,对函数y=+x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y=+x中自变量x的取值范围是 .
(2)下表是y与x的几组对应值,请直接写出m的值: .
x … -2 -1 0 1 3 4 5 6 …
y … - - - 0 - - m …
(3)在如图示的平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象.
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与直线x=2越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.
答案
1.A
2.C ∵点A(2,-3),点A与点B关于原点对称,∴点B的坐标为(-2,3).∵反比例函数的图象经过点B,∴反比例函数的表达式是y=-.
3.y= 由题意,得y=,即y=.
4.C
5.D ∵反比例函数的图象在第一、三象限,∴a-2>0,∴a>2.故选D.
6.B 7.C
8.B 如图图,过点B作BE⊥x轴于点E.
∵AC⊥x轴,
∴AC∥BE,
可得△OCD∽△OEB,
∴==.
∵D为OB的中点,
∴OD=OB,
∴OC=OE,CD=BE.
设A,则B,CD=,
∴AD=-.
∵△ADO的面积为1.
∴AD·OC=1,
即·x=1,
解得k=.故选B.
9.D
10.解:(1)∵点A(-2,4)在反比例函数y=的图象上,
∴k2=-8.
∴反比例函数的表达式为y=-.
(2)∵点B的横坐标为-4,
∴其纵坐标为2,
∴B(-4,2).
∵点A(-2,4),B(-4,2)在直线y=k1x+b上,
∴ 解得
∴直线AB的函数表达式为y=x+6,它与x轴的交点C的坐标为(-6,0),
∴S△AOC=×6×4=12.
11.A ∵剪去两个一样的小矩形,两个矩形的面积和为20,∴xy=10,∴y是x的反比例函数.∵2≤x≤10,∴答案为A.
12.解:(1)依题意,得xy=32,∴y=.
(2)不能.理由:当y=8.5时,=8.5,
∴x=,∴x+2y=20.
∵20>20,∴对于(1)中的函数y的值不能取到8.5.
13.解:(1)由题意得x-2≠0,解得x≠2.故答案为x≠2.
(2)当x=3时,m=+3=1+3=4.故答案为4.
(3)图象如图图所示.
(4)①(2,2) ②y=x
同课章节目录
