北师大版数学九年级上册同步课时练习:1.1 第3课时 菱形的性质与判定的综合应用 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:1.1 第3课时 菱形的性质与判定的综合应用 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 06:48:27 | ||
图片预览


文档简介
第3课时 菱形的性质与判定的综合应用
知识点 1 菱形的面积
1.已知菱形的两条对角线长分别是12和16,则这个菱形的面积是 ( )
A.192 B.96 C.48 D.40
2.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O.若BD=6,则菱形ABCD的面积是 ( )
A.6 B.12 C.24 D.48
3.[教材例3变式题] 如图,在菱形ABCD中,已知AB=17 cm,BD=30 cm,AC,BD交于点O,求菱形ABCD的面积.
知识点 2 菱形的性质与判定的应用
4.下列说法中不正确的是 ( )
A.四边相等的四边形是菱形
B.对角线互相垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
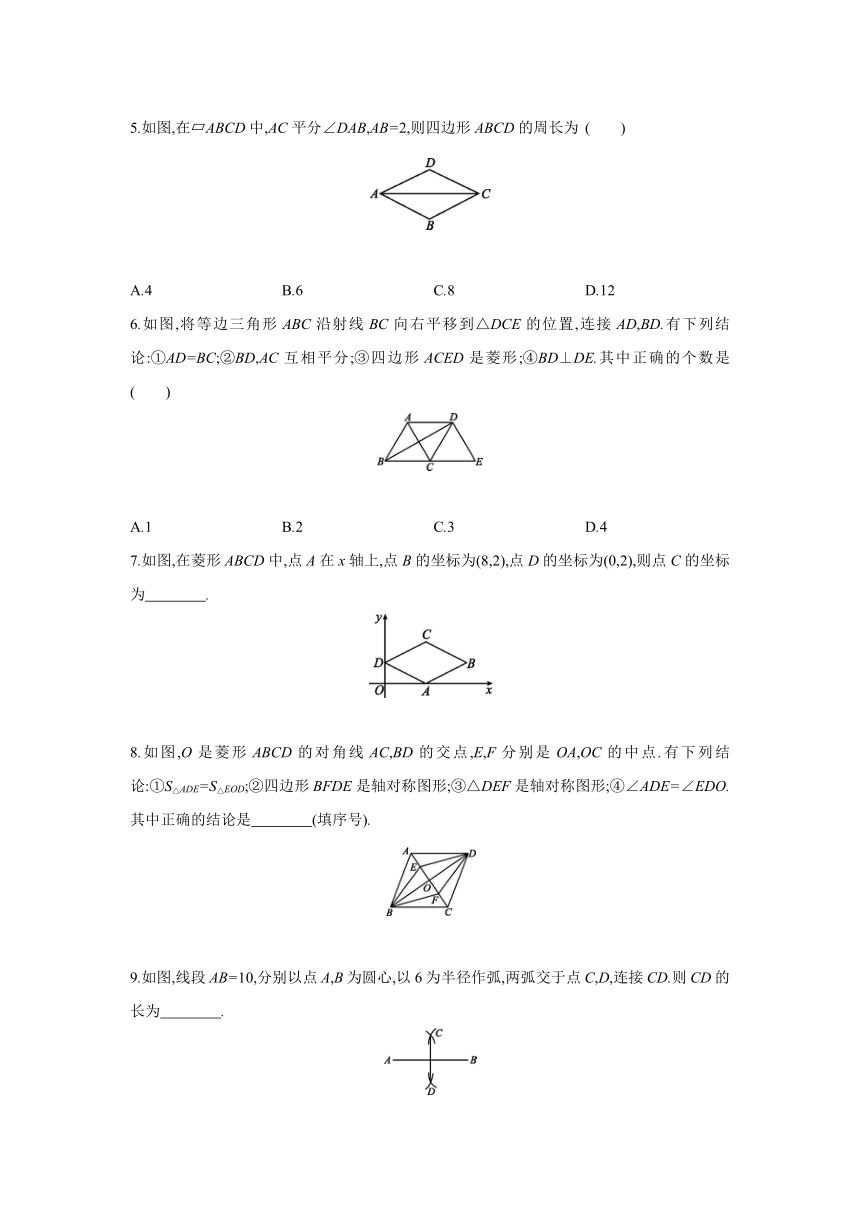
5.如图,在 ABCD中,AC平分∠DAB,AB=2,则四边形ABCD的周长为 ( )
A.4 B.6 C.8 D.12
6.如图,将等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD,BD.有下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形;④BD⊥DE.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
7.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
8.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.有下列结论:①S△ADE=S△EOD;②四边形BFDE是轴对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中正确的结论是 (填序号).
9.如图,线段AB=10,分别以点A,B为圆心,以6为半径作弧,两弧交于点C,D,连接CD.则CD的长为 .
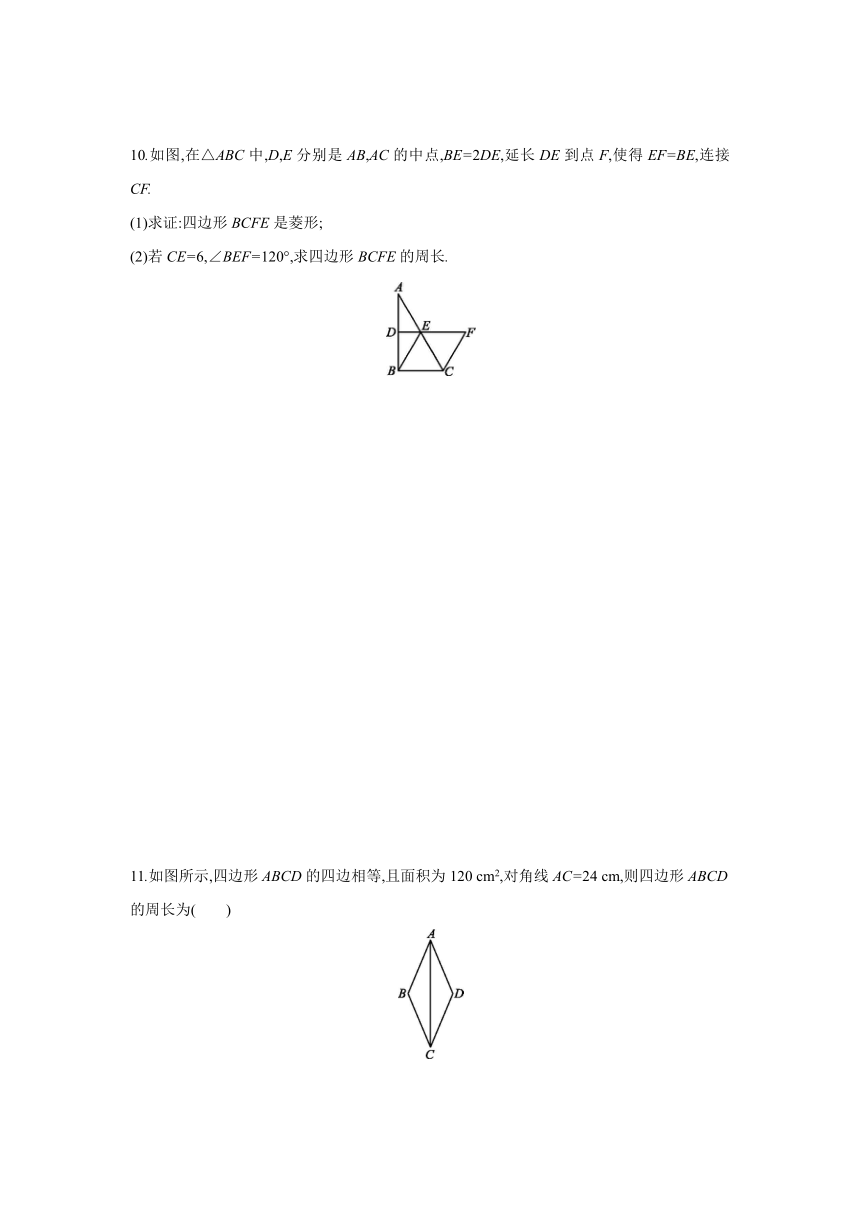
10.如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求四边形BCFE的周长.
11.如图所示,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为( )
A.52 cm B.40 cm C.39 cm D.26 cm
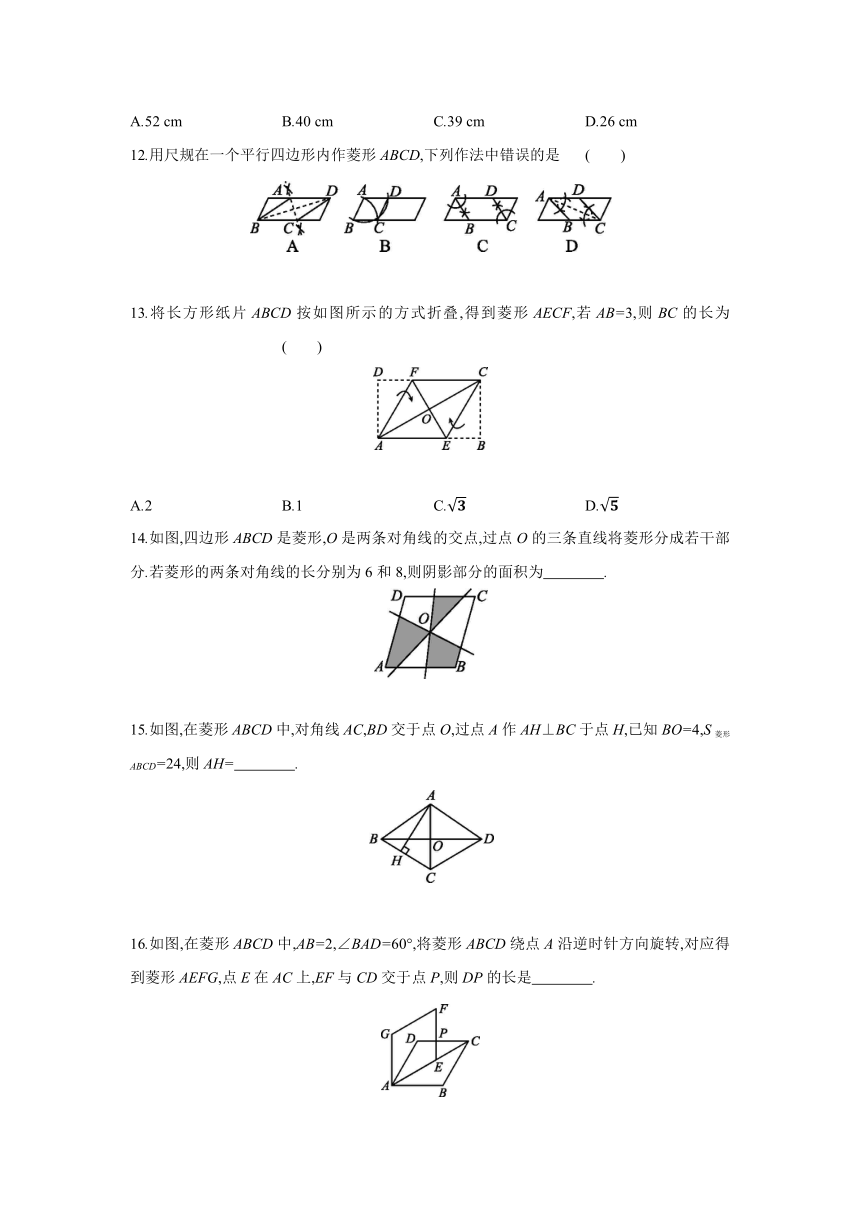
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是 ( )
13.将长方形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为 ( )
A.2 B.1 C. D.
14.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成若干部分.若菱形的两条对角线的长分别为6和8,则阴影部分的面积为 .
15.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH= .
16.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A沿逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是 .
17.如图,已知等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,与AC,BC分别交于点E,F,作PM∥AC,交AB于点M,连接ME.
(1)求证:四边形AEPM为菱形;
(2)当点P位于何处时,菱形AEPM的面积为四边形EFBM面积的一半
18.[教材“做一做”变式题] 明明将两张长为8 cm、宽为2 cm的长方形纸条交叉叠放,如图①所示,他发现重叠部分是一个菱形.
(1)请你帮助明明证明重叠部分(四边形ABCD)是菱形;
(2)明明又发现:如图图②所示,当菱形的一条对角线与长方形纸条的一条对角线重合时,菱形ABCD的周长最大,求此时菱形ABCD的周长.
答案
1.B 2.C
3.解:∵四边形ABCD为菱形,BD=30 cm,
∴BO=BD=15 cm,AO=AC,AC⊥BD.
在Rt△AOB中,
由勾股定理,得AO===8(cm),
∴AC=16 cm,
∴S菱形ABCD=AC·BD=×16×30=240(cm2).
4.C 菱形的对角线互相垂直且互相平分,不一定相等,故选C.
5.C 6.D
7.(4,4) 连接BD,AC交于点E.根据点B的坐标为(8,2),点D的坐标为(0,2),可知BD∥x轴.因为四边形ABCD是菱形,所以AC⊥BD,AE=CE=OD=2,DE=BE=OA=4,所以AC=4,故点C的坐标为(4,4).
8.①②③ ①∵E是OA的中点,∴AE=OE.∵△ADE与△EOD等高,∴S△ADE=S△EOD.故①正确.②∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.∵E,F分别是OA,OC的中点,∴OE=OF,∴四边形BFDE是平行四边形.又∵EF⊥BD,∴平行四边形BFDE是菱形,∴四边形BFDE是轴对称图形.故②正确.③∵OE=OF,AC⊥BD,∴△DEF是等腰三角形,∴△DEF是轴对称图形.故③正确.④∵AD>OD,AE=OE,∴∠ADE≠∠EDO,故④错误.
9.2 如图图,顺次连接点A,C,B,D,设AB与CD交于点O.∵分别以点A,B为圆心,以6为半径作弧,两弧交于点C,D,
∴AC=AD=BC=BD=6,
∴四边形ACBD是菱形,
∴AB⊥CD,OA=OB=AB=5,OC=OD.
∴在Rt△AOC中,
OC===,
∴CD=2OC=2.
故答案为2.
10.解:(1)证明:∵D,E分别是AB,AC的中点,
∴DE∥BC且BC=2DE.
又∵BE=2DE,EF=BE,∴EF=BC.
又∵DE∥BC,即EF∥BC,
∴四边形BCFE是平行四边形.
又∵BE=EF,∴ BCFE是菱形.
(2)由(1)知EF∥BC,
∴∠EBC+∠BEF=180°.
∵∠BEF=120°,
∴∠EBC=60°.
又由(1)知BE=BC,
∴△BEC是等边三角形,
∴BE=CE=6,
∴菱形BCFE的周长为6×4=24.
11.A 如图图,连接BD与AC相交于点O.
∵四边形ABCD的四边相等,∴四边形ABCD为菱形,∴S菱形ABCD=AC·BD,AC⊥BD,
∴×24·BD=120,解得BD=10(cm),∴OA=12 cm,OB=5 cm.
在Rt△AOB中,由勾股定理,得AB==13(cm),∴四边形ABCD的周长为4×13=52(cm).故选A.
12.C 13.C
14.12 对图中的点进行标注.
∵菱形ABCD的两条对角线的长分别为6和8,∴菱形ABCD的面积=×6×8=24.∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴点M,E,G分别是点N,F,H关于点O的对称点,∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,∴S△OEG=S△OFH,S四边形OMAH=S四边形ONCG,S四边形OEDM=S四边形OFBN,∴阴影部分的面积=S菱形ABCD=×24=12.
15. ∵四边形ABCD是菱形,
∴BO=DO=4,AO=CO,AC⊥BD,∴BD=8.
∵S菱形ABCD=AC·BD=24,∴AC=6,
∴OC=AC=3,∴BC==5.
∵S菱形ABCD=BC·AH=24,∴AH=.
故答案为.
16.-1 连接BD交AC于点O,如图图所示.
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA==,∴AC=2.
由旋转的性质得AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC-AE=2-2.
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE=-1.
由勾股定理得PC==3-,
∴DP=CD-PC=2-(3-)=-1.
故答案为-1.
17.解:(1)证明:∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∵AD平分∠BAC,∴∠CAD=∠BAD.
∵EF∥AB,∴∠BAD=∠EPA,
∴∠CAD=∠EPA,
∴EA=EP,∴ AEPM为菱形.
(2)当P为EF的中点时,S菱形AEPM=S四边形EFBM.
∵四边形AEPM为菱形,∴AD⊥EM.
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∴EM∥BC.
又∵EF∥AB,∴四边形EFBM为平行四边形.
如图图,过点M作MN⊥EF于点N,
则S菱形AEPM=EP·MN,S四边形EFBM=EF·MN.
当P为EF的中点时,EP=EF,
此时S菱形AEPM=S四边形EFBM.
18.解:(1)证明:如图图①所示,过点A作AE⊥BC于点E,AF⊥CD于点F.
∵两张长方形纸条的宽度相同,
∴AB∥CD,AD∥BC,AE=AF,
∴四边形ABCD是平行四边形.
∵S ABCD=BC·AE=CD·AF,AE=AF,
∴BC=CD,
∴ ABCD是菱形.
(2)如图图②所示,设CD=BC=x cm,
则CE=(8-x)cm.
在Rt△DCE中,CD2=DE2+CE2,
即x2=22+(8-x)2,
解得x=.
4×=17(cm),
故此时菱形ABCD的周长为17 cm.
知识点 1 菱形的面积
1.已知菱形的两条对角线长分别是12和16,则这个菱形的面积是 ( )
A.192 B.96 C.48 D.40
2.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O.若BD=6,则菱形ABCD的面积是 ( )
A.6 B.12 C.24 D.48
3.[教材例3变式题] 如图,在菱形ABCD中,已知AB=17 cm,BD=30 cm,AC,BD交于点O,求菱形ABCD的面积.
知识点 2 菱形的性质与判定的应用
4.下列说法中不正确的是 ( )
A.四边相等的四边形是菱形
B.对角线互相垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
5.如图,在 ABCD中,AC平分∠DAB,AB=2,则四边形ABCD的周长为 ( )
A.4 B.6 C.8 D.12
6.如图,将等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD,BD.有下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形;④BD⊥DE.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
7.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
8.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.有下列结论:①S△ADE=S△EOD;②四边形BFDE是轴对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中正确的结论是 (填序号).
9.如图,线段AB=10,分别以点A,B为圆心,以6为半径作弧,两弧交于点C,D,连接CD.则CD的长为 .
10.如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求四边形BCFE的周长.
11.如图所示,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为( )
A.52 cm B.40 cm C.39 cm D.26 cm
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是 ( )
13.将长方形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则BC的长为 ( )
A.2 B.1 C. D.
14.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成若干部分.若菱形的两条对角线的长分别为6和8,则阴影部分的面积为 .
15.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH= .
16.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A沿逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是 .
17.如图,已知等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,与AC,BC分别交于点E,F,作PM∥AC,交AB于点M,连接ME.
(1)求证:四边形AEPM为菱形;
(2)当点P位于何处时,菱形AEPM的面积为四边形EFBM面积的一半
18.[教材“做一做”变式题] 明明将两张长为8 cm、宽为2 cm的长方形纸条交叉叠放,如图①所示,他发现重叠部分是一个菱形.
(1)请你帮助明明证明重叠部分(四边形ABCD)是菱形;
(2)明明又发现:如图图②所示,当菱形的一条对角线与长方形纸条的一条对角线重合时,菱形ABCD的周长最大,求此时菱形ABCD的周长.
答案
1.B 2.C
3.解:∵四边形ABCD为菱形,BD=30 cm,
∴BO=BD=15 cm,AO=AC,AC⊥BD.
在Rt△AOB中,
由勾股定理,得AO===8(cm),
∴AC=16 cm,
∴S菱形ABCD=AC·BD=×16×30=240(cm2).
4.C 菱形的对角线互相垂直且互相平分,不一定相等,故选C.
5.C 6.D
7.(4,4) 连接BD,AC交于点E.根据点B的坐标为(8,2),点D的坐标为(0,2),可知BD∥x轴.因为四边形ABCD是菱形,所以AC⊥BD,AE=CE=OD=2,DE=BE=OA=4,所以AC=4,故点C的坐标为(4,4).
8.①②③ ①∵E是OA的中点,∴AE=OE.∵△ADE与△EOD等高,∴S△ADE=S△EOD.故①正确.②∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.∵E,F分别是OA,OC的中点,∴OE=OF,∴四边形BFDE是平行四边形.又∵EF⊥BD,∴平行四边形BFDE是菱形,∴四边形BFDE是轴对称图形.故②正确.③∵OE=OF,AC⊥BD,∴△DEF是等腰三角形,∴△DEF是轴对称图形.故③正确.④∵AD>OD,AE=OE,∴∠ADE≠∠EDO,故④错误.
9.2 如图图,顺次连接点A,C,B,D,设AB与CD交于点O.∵分别以点A,B为圆心,以6为半径作弧,两弧交于点C,D,
∴AC=AD=BC=BD=6,
∴四边形ACBD是菱形,
∴AB⊥CD,OA=OB=AB=5,OC=OD.
∴在Rt△AOC中,
OC===,
∴CD=2OC=2.
故答案为2.
10.解:(1)证明:∵D,E分别是AB,AC的中点,
∴DE∥BC且BC=2DE.
又∵BE=2DE,EF=BE,∴EF=BC.
又∵DE∥BC,即EF∥BC,
∴四边形BCFE是平行四边形.
又∵BE=EF,∴ BCFE是菱形.
(2)由(1)知EF∥BC,
∴∠EBC+∠BEF=180°.
∵∠BEF=120°,
∴∠EBC=60°.
又由(1)知BE=BC,
∴△BEC是等边三角形,
∴BE=CE=6,
∴菱形BCFE的周长为6×4=24.
11.A 如图图,连接BD与AC相交于点O.
∵四边形ABCD的四边相等,∴四边形ABCD为菱形,∴S菱形ABCD=AC·BD,AC⊥BD,
∴×24·BD=120,解得BD=10(cm),∴OA=12 cm,OB=5 cm.
在Rt△AOB中,由勾股定理,得AB==13(cm),∴四边形ABCD的周长为4×13=52(cm).故选A.
12.C 13.C
14.12 对图中的点进行标注.
∵菱形ABCD的两条对角线的长分别为6和8,∴菱形ABCD的面积=×6×8=24.∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴点M,E,G分别是点N,F,H关于点O的对称点,∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,∴S△OEG=S△OFH,S四边形OMAH=S四边形ONCG,S四边形OEDM=S四边形OFBN,∴阴影部分的面积=S菱形ABCD=×24=12.
15. ∵四边形ABCD是菱形,
∴BO=DO=4,AO=CO,AC⊥BD,∴BD=8.
∵S菱形ABCD=AC·BD=24,∴AC=6,
∴OC=AC=3,∴BC==5.
∵S菱形ABCD=BC·AH=24,∴AH=.
故答案为.
16.-1 连接BD交AC于点O,如图图所示.
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA==,∴AC=2.
由旋转的性质得AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC-AE=2-2.
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE=-1.
由勾股定理得PC==3-,
∴DP=CD-PC=2-(3-)=-1.
故答案为-1.
17.解:(1)证明:∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∵AD平分∠BAC,∴∠CAD=∠BAD.
∵EF∥AB,∴∠BAD=∠EPA,
∴∠CAD=∠EPA,
∴EA=EP,∴ AEPM为菱形.
(2)当P为EF的中点时,S菱形AEPM=S四边形EFBM.
∵四边形AEPM为菱形,∴AD⊥EM.
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∴EM∥BC.
又∵EF∥AB,∴四边形EFBM为平行四边形.
如图图,过点M作MN⊥EF于点N,
则S菱形AEPM=EP·MN,S四边形EFBM=EF·MN.
当P为EF的中点时,EP=EF,
此时S菱形AEPM=S四边形EFBM.
18.解:(1)证明:如图图①所示,过点A作AE⊥BC于点E,AF⊥CD于点F.
∵两张长方形纸条的宽度相同,
∴AB∥CD,AD∥BC,AE=AF,
∴四边形ABCD是平行四边形.
∵S ABCD=BC·AE=CD·AF,AE=AF,
∴BC=CD,
∴ ABCD是菱形.
(2)如图图②所示,设CD=BC=x cm,
则CE=(8-x)cm.
在Rt△DCE中,CD2=DE2+CE2,
即x2=22+(8-x)2,
解得x=.
4×=17(cm),
故此时菱形ABCD的周长为17 cm.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
