北师大版数学九年级上册同步课时练习:1.2 第3课时矩形的性质与判定的综合应用 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:1.2 第3课时矩形的性质与判定的综合应用 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 07:02:49 | ||
图片预览


文档简介
第3课时 矩形的性质与判定的综合应用
知识点 矩形的性质与判定的综合应用
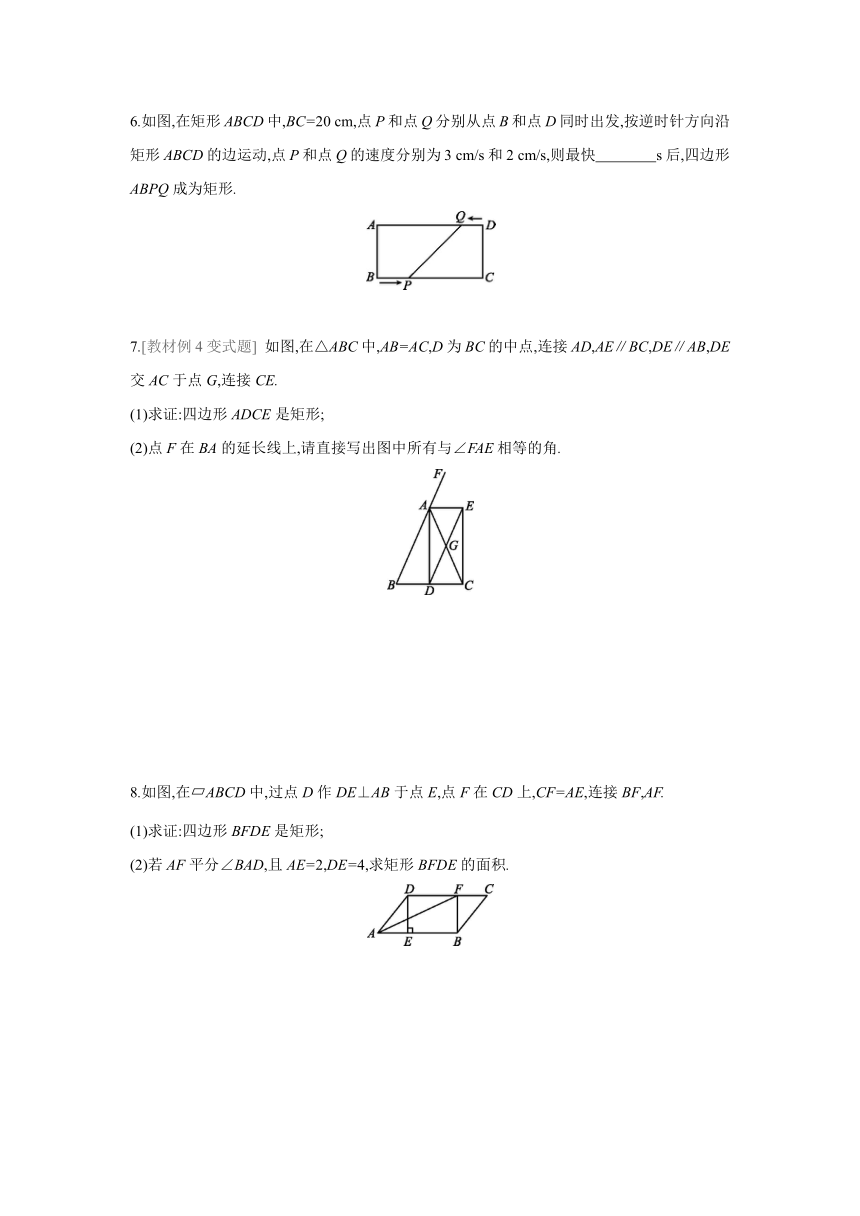
1.下列结论中,矩形具有而菱形不一定具有的性质是 ( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为 ( )
A. cm B.2 cm C.2 cm D.4 cm
3.如图,在矩形ABCD中,O为对角线的交点,E为BC的中点,OE=3,AC=12,则AD的长为 ( )
A.6 B.8 C.6 D.6
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于点E,则∠BOE的度数为 .
5.将一个含30°角的三角尺(∠EMF=90°)按如图所示放置在矩形纸板上(三角尺的直角边EM过矩形ABCD的顶点A,点D与点F重合),已知矩形纸板的长是宽的2倍,M是BC边的中点,则∠AFE的度数为 .
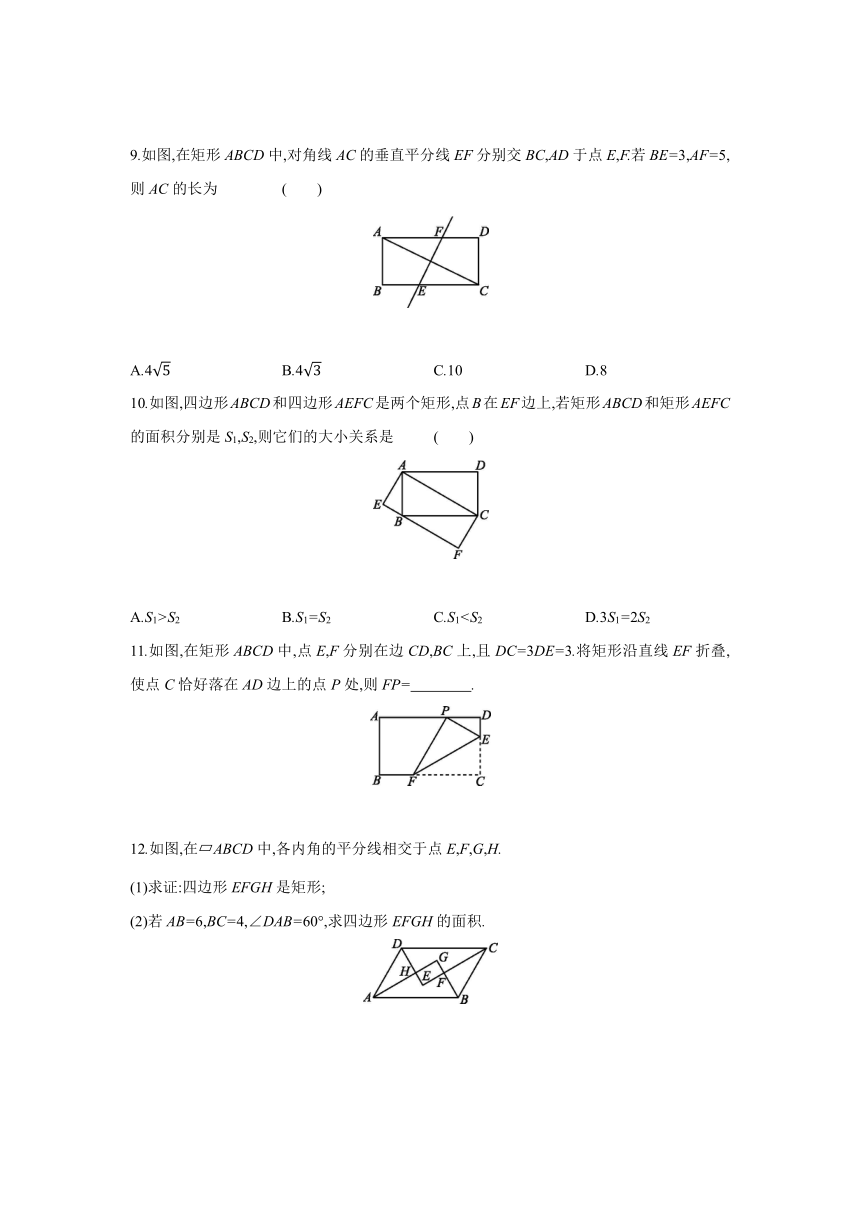
6.如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.
7.[教材例4变式题] 如图,在△ABC中,AB=AC,D为BC的中点,连接AD,AE∥BC,DE∥AB,DE交AC于点G,连接CE.
(1)求证:四边形ADCE是矩形;
(2)点F在BA的延长线上,请直接写出图中所有与∠FAE相等的角.
8.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=2,DE=4,求矩形BFDE的面积.
9.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为 ( )
A.4 B.4 C.10 D.8
10.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则它们的大小关系是 ( )
A.S1>S2 B.S1=S2 C.S111.如图,在矩形ABCD中,点E,F分别在边CD,BC上,且DC=3DE=3.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
12.如图,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
13.如图①所示,矩形ABCD中,AC与BD交于点O,且P为AD的中点,PE⊥OA于点E,PF⊥OD于点F,AB=6 cm,AD=8 cm.
(1)求出PE+PF的值;
(2)若P是AD边上任意一点,其他条件不变,如图②,求出PE+PF的值.
答案
1.C 矩形的对角线相等且互相平分,菱形的对角线互相垂直且平分,所以矩形具有而菱形不具有的性质为对角线相等.故选C.
2.D ∵四边形ABCD为矩形,
∴AC=BD,OA=OB=AC=4 cm.
∵∠AOD=120°,∴∠AOB=60°,
∴△AOB是等边三角形,∴AB=OA=4 cm.
3.A ∵四边形ABCD为矩形,
∴AD=BC,OB=OC=AC=6.
∵OB=OC,BE=EC,∴OE⊥BC,
∴EC==3,
∴AD=BC=2EC=6.故选A.
4.75° ∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB.
又∵∠AOB=60°,∴△AOB是等边三角形,
∴AB=OB,∠ABO=60°,∴∠OBE=30°.∵AE平分∠BAD,
∴∠BAE=45°,∴△ABE是等腰直角三角形,∴AB=BE,∴BE=OB,∴∠BOE=×(180°-30°)=75°.
5.15° ∵四边形ABCD为矩形,∴∠B=∠BAD=90°.∵BC=2AB,M是BC边的中点,∴AB=BM,∴∠BAM=45°=∠DAM,∴∠E+∠AFE=45°.∵∠E=30°,∴∠AFE=15°.
6.4 设最快x s后,四边形ABPQ成为矩形,由BP=AQ,得3x=20-2x,解得x=4.
7.解:(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,∴AE=BD.
∵D为BC的中点,∴BD=CD,∴AE=CD.
又∵AE∥BC,
∴四边形ADCE是平行四边形.
∵AB=AC,D为BC的中点,
∴AD⊥BC,即∠ADC=90°,
∴ ADCE是矩形.
(2)∵AB=AC,∴∠B=∠ACB.
∵DE∥AB,∴∠B=∠EDC.
∵AE∥BC,
∴∠AED=∠EDC,∠EAC=∠ACB,
∠FAE=∠B,
∴∠FAE=∠B=∠ACB=∠EDC=∠AED=∠EAC.
8.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DF∥BE.
∵CF=AE,∴DF=BE,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形.
(2)∵AB∥CD,∴∠BAF=∠AFD.
∵AF平分∠BAD,∴∠DAF=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF.
在Rt△ADE中,∵AE=2,DE=4,
∴AD===2,
∴DF=2,
∴矩形BFDE的面积=DF·DE=2×4=8.
9.A 连接AE,如图图.
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE.
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,
∵∠AOF=∠COE,OA=OC,∠OAF=∠OCE,
∴△AOF≌△COE(ASA),∴AF=CE=5,
∴AE=CE=5,BC=BE+CE=3+5=8,
从而AB===4,
∴AC===4.
故选A.
10.B 矩形ABCD的面积S1=2S△ABC,而矩形AEFC的面积S2=AC·AE,S△ABC=AC·AE,故S2=2S△ABC,即S1=S2.故选B.
11.2 ∵DC=3DE=3,∴DE=1,CE=2.由翻折的性质得,PE=CE,FP=FC,∠EPF=∠C=90°,∠CFE=∠PFE,∴PE=2.
又∵∠D=90°,∴∠DPE=30°,∴∠DPF=∠EPF+∠DPE=90°+30°=120°.
∵矩形ABCD中,AD∥BC,∴∠CFP=180°-∠DPF=180°-120°=60°,
∴∠CFE=∠CFP=×60°=30°,∴EF=2CE=2×2=4.
在Rt△CEF中,根据勾股定理,得FC==2.故FP=FC=2.
12.解:(1)证明:∵AG平分∠DAB,BG平分∠ABC,
∴∠GAB=∠DAB,∠GBA=∠ABC.
∵在 ABCD中,∠DAB+∠ABC=180°,
∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,
∴∠AGB=90°.
同理可得,∠DEC=90°,∠AHD=90°=∠EHG,
∴四边形EFGH是矩形.
(2)∵ ABCD中,∠DAB=60°,
∴∠BCD=60°.
由(1),得∠GAB=∠DAB=30°.
∵AB=6,
∴BG=AB=3,易得AG=3=CE.
∵BC=4,∠BCF=∠BCD=30°,
∴BF=BC=2,CF=2,
∴EF=CE-CF=3-2=,GF=BG-BF=3-2=1,
∴矩形EFGH的面积=EF·GF=.
13.解:(1)连接OP,如图图①所示.
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,CD=AB=6 cm,OA=OC=OB=OD,
∴AC===10(cm),
∴OA=OD=5 cm.
∵P为AD的中点,∴OP是△ACD的中位线,
∴OP∥CD,OP=CD=3 cm,
从而∠OPD=90°,即OP⊥AD,
∴△AOD的面积=AD·OP=×8×3=12(cm2).
又∵△AOD的面积=△OAP的面积+△ODP的面积=OA·PE+OD·PF=(PE+PF)×5=12,
∴PE+PF=(cm).
(2)连接OP,如图图②所示.
∵△AOD的面积=△OAP的面积+△ODP的面积=OA·PE+OD·PF.
由(1),得OA=OD=5 cm,且易得△AOD的面积=×矩形ABCD的面积=×6×8=12(cm2).
∴×5(PE+PF)=12,
∴PE+PF=(cm).
知识点 矩形的性质与判定的综合应用
1.下列结论中,矩形具有而菱形不一定具有的性质是 ( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为 ( )
A. cm B.2 cm C.2 cm D.4 cm
3.如图,在矩形ABCD中,O为对角线的交点,E为BC的中点,OE=3,AC=12,则AD的长为 ( )
A.6 B.8 C.6 D.6
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于点E,则∠BOE的度数为 .
5.将一个含30°角的三角尺(∠EMF=90°)按如图所示放置在矩形纸板上(三角尺的直角边EM过矩形ABCD的顶点A,点D与点F重合),已知矩形纸板的长是宽的2倍,M是BC边的中点,则∠AFE的度数为 .
6.如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快 s后,四边形ABPQ成为矩形.
7.[教材例4变式题] 如图,在△ABC中,AB=AC,D为BC的中点,连接AD,AE∥BC,DE∥AB,DE交AC于点G,连接CE.
(1)求证:四边形ADCE是矩形;
(2)点F在BA的延长线上,请直接写出图中所有与∠FAE相等的角.
8.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=2,DE=4,求矩形BFDE的面积.
9.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为 ( )
A.4 B.4 C.10 D.8
10.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则它们的大小关系是 ( )
A.S1>S2 B.S1=S2 C.S1
12.如图,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
13.如图①所示,矩形ABCD中,AC与BD交于点O,且P为AD的中点,PE⊥OA于点E,PF⊥OD于点F,AB=6 cm,AD=8 cm.
(1)求出PE+PF的值;
(2)若P是AD边上任意一点,其他条件不变,如图②,求出PE+PF的值.
答案
1.C 矩形的对角线相等且互相平分,菱形的对角线互相垂直且平分,所以矩形具有而菱形不具有的性质为对角线相等.故选C.
2.D ∵四边形ABCD为矩形,
∴AC=BD,OA=OB=AC=4 cm.
∵∠AOD=120°,∴∠AOB=60°,
∴△AOB是等边三角形,∴AB=OA=4 cm.
3.A ∵四边形ABCD为矩形,
∴AD=BC,OB=OC=AC=6.
∵OB=OC,BE=EC,∴OE⊥BC,
∴EC==3,
∴AD=BC=2EC=6.故选A.
4.75° ∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB.
又∵∠AOB=60°,∴△AOB是等边三角形,
∴AB=OB,∠ABO=60°,∴∠OBE=30°.∵AE平分∠BAD,
∴∠BAE=45°,∴△ABE是等腰直角三角形,∴AB=BE,∴BE=OB,∴∠BOE=×(180°-30°)=75°.
5.15° ∵四边形ABCD为矩形,∴∠B=∠BAD=90°.∵BC=2AB,M是BC边的中点,∴AB=BM,∴∠BAM=45°=∠DAM,∴∠E+∠AFE=45°.∵∠E=30°,∴∠AFE=15°.
6.4 设最快x s后,四边形ABPQ成为矩形,由BP=AQ,得3x=20-2x,解得x=4.
7.解:(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,∴AE=BD.
∵D为BC的中点,∴BD=CD,∴AE=CD.
又∵AE∥BC,
∴四边形ADCE是平行四边形.
∵AB=AC,D为BC的中点,
∴AD⊥BC,即∠ADC=90°,
∴ ADCE是矩形.
(2)∵AB=AC,∴∠B=∠ACB.
∵DE∥AB,∴∠B=∠EDC.
∵AE∥BC,
∴∠AED=∠EDC,∠EAC=∠ACB,
∠FAE=∠B,
∴∠FAE=∠B=∠ACB=∠EDC=∠AED=∠EAC.
8.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DF∥BE.
∵CF=AE,∴DF=BE,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形.
(2)∵AB∥CD,∴∠BAF=∠AFD.
∵AF平分∠BAD,∴∠DAF=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF.
在Rt△ADE中,∵AE=2,DE=4,
∴AD===2,
∴DF=2,
∴矩形BFDE的面积=DF·DE=2×4=8.
9.A 连接AE,如图图.
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE.
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,
∵∠AOF=∠COE,OA=OC,∠OAF=∠OCE,
∴△AOF≌△COE(ASA),∴AF=CE=5,
∴AE=CE=5,BC=BE+CE=3+5=8,
从而AB===4,
∴AC===4.
故选A.
10.B 矩形ABCD的面积S1=2S△ABC,而矩形AEFC的面积S2=AC·AE,S△ABC=AC·AE,故S2=2S△ABC,即S1=S2.故选B.
11.2 ∵DC=3DE=3,∴DE=1,CE=2.由翻折的性质得,PE=CE,FP=FC,∠EPF=∠C=90°,∠CFE=∠PFE,∴PE=2.
又∵∠D=90°,∴∠DPE=30°,∴∠DPF=∠EPF+∠DPE=90°+30°=120°.
∵矩形ABCD中,AD∥BC,∴∠CFP=180°-∠DPF=180°-120°=60°,
∴∠CFE=∠CFP=×60°=30°,∴EF=2CE=2×2=4.
在Rt△CEF中,根据勾股定理,得FC==2.故FP=FC=2.
12.解:(1)证明:∵AG平分∠DAB,BG平分∠ABC,
∴∠GAB=∠DAB,∠GBA=∠ABC.
∵在 ABCD中,∠DAB+∠ABC=180°,
∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,
∴∠AGB=90°.
同理可得,∠DEC=90°,∠AHD=90°=∠EHG,
∴四边形EFGH是矩形.
(2)∵ ABCD中,∠DAB=60°,
∴∠BCD=60°.
由(1),得∠GAB=∠DAB=30°.
∵AB=6,
∴BG=AB=3,易得AG=3=CE.
∵BC=4,∠BCF=∠BCD=30°,
∴BF=BC=2,CF=2,
∴EF=CE-CF=3-2=,GF=BG-BF=3-2=1,
∴矩形EFGH的面积=EF·GF=.
13.解:(1)连接OP,如图图①所示.
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,CD=AB=6 cm,OA=OC=OB=OD,
∴AC===10(cm),
∴OA=OD=5 cm.
∵P为AD的中点,∴OP是△ACD的中位线,
∴OP∥CD,OP=CD=3 cm,
从而∠OPD=90°,即OP⊥AD,
∴△AOD的面积=AD·OP=×8×3=12(cm2).
又∵△AOD的面积=△OAP的面积+△ODP的面积=OA·PE+OD·PF=(PE+PF)×5=12,
∴PE+PF=(cm).
(2)连接OP,如图图②所示.
∵△AOD的面积=△OAP的面积+△ODP的面积=OA·PE+OD·PF.
由(1),得OA=OD=5 cm,且易得△AOD的面积=×矩形ABCD的面积=×6×8=12(cm2).
∴×5(PE+PF)=12,
∴PE+PF=(cm).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
