北师大版数学九年级上册同步课时练习:1.3 第1课时 正方形的性质 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:1.3 第1课时 正方形的性质 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 06:54:07 | ||
图片预览

文档简介
3 第1课时 正方形的性质
知识点 1 利用正方形的性质求解与线段有关的问题
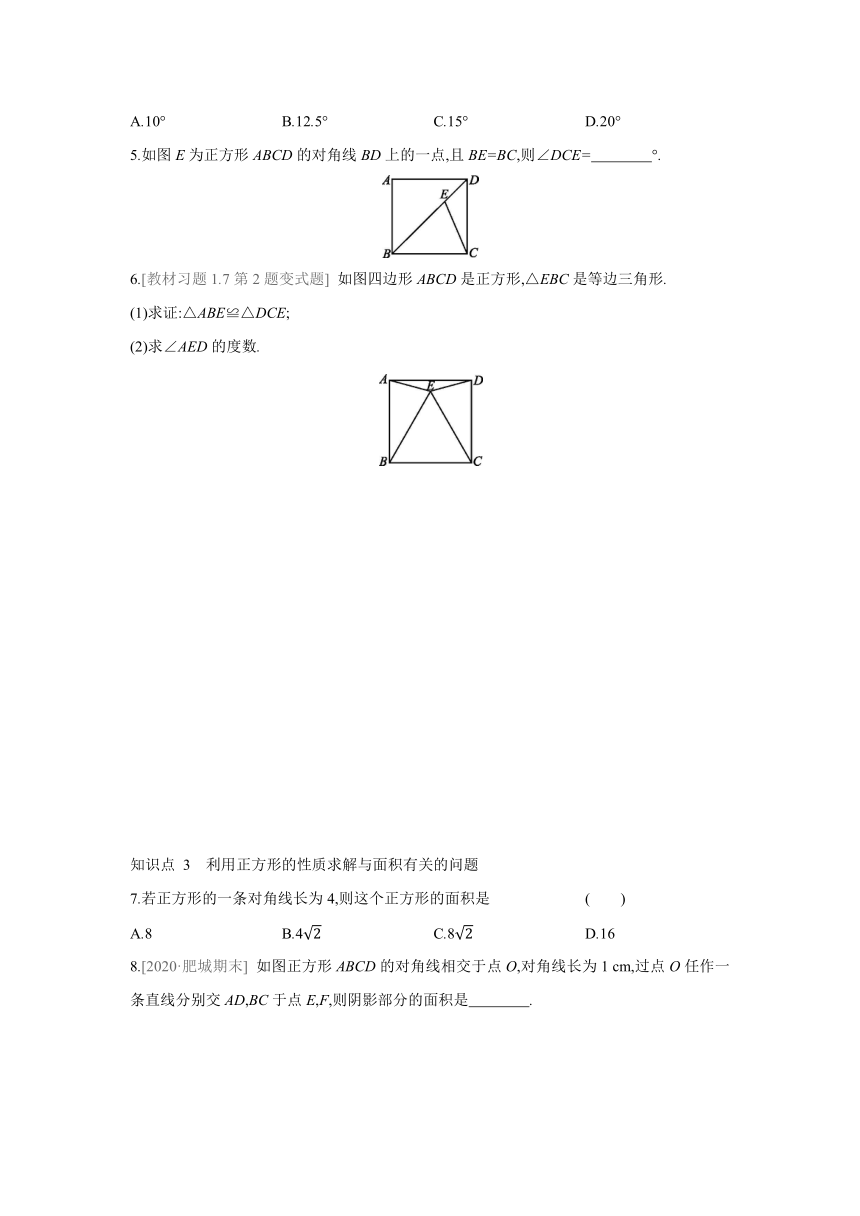
1.如图在正方形ABCD中,点E在边DC上,DE=4,EC=2,则AE的长为 .
2.如图正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,垂足为F,那么FC= .
3.如图四边形ABCD是正方形,E,F分别是AB,AD上的点,且BF⊥CE,垂足为G.求证:CE=BF.
知识点 2 利用正方形的性质求解与角有关的问题
4.如图在正方形ABCD的外侧作等边三角形ADE,则∠AEB的度数为 ( )
A.10° B.12.5° C.15° D.20°
5.如图E为正方形ABCD的对角线BD上的一点,且BE=BC,则∠DCE= °.
6.[教材习题1.7第2题变式题] 如图四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
知识点 3 利用正方形的性质求解与面积有关的问题
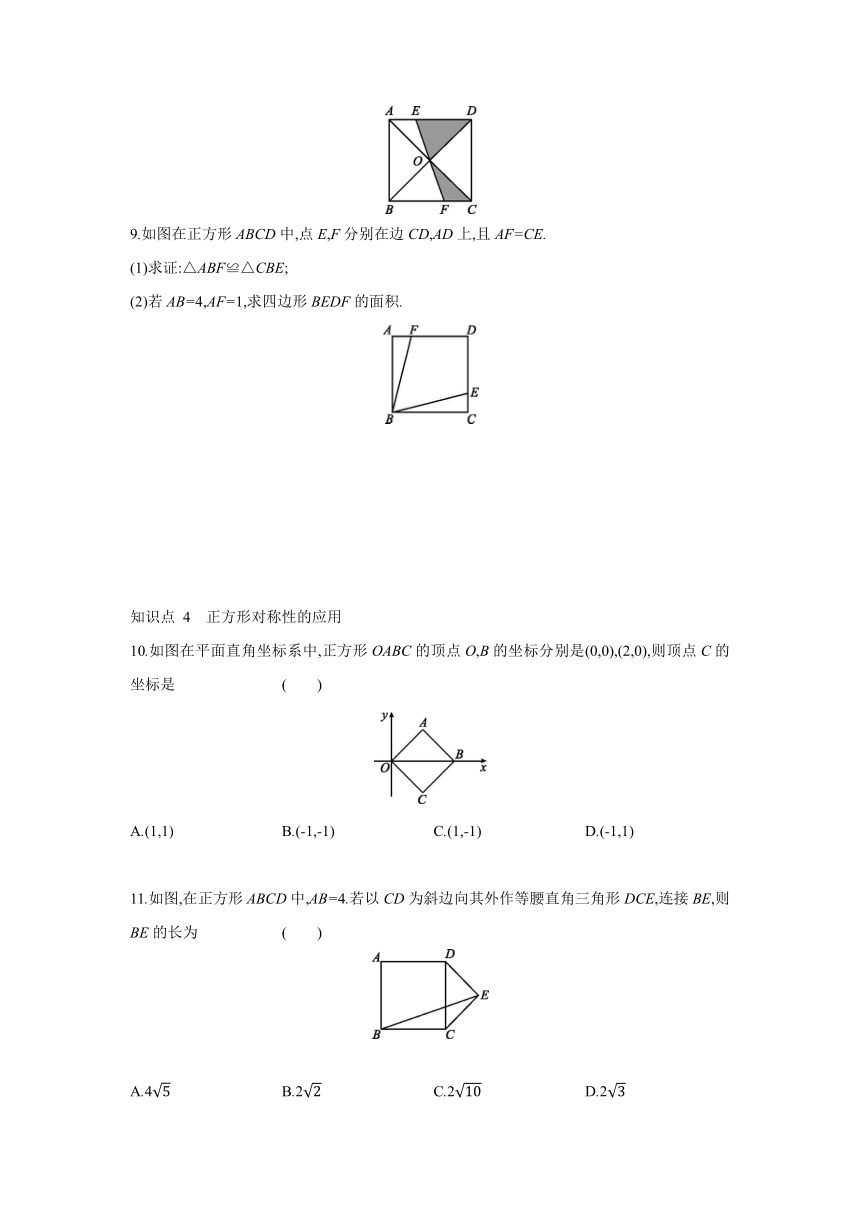
7.若正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
8.[2020·肥城期末] 如图正方形ABCD的对角线相交于点O,对角线长为1 cm,过点O任作一条直线分别交AD,BC于点E,F,则阴影部分的面积是 .
9.如图在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.
(1)求证:△ABF≌△CBE;
(2)若AB=4,AF=1,求四边形BEDF的面积.
知识点 4 正方形对称性的应用
10.如图在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(2,0),则顶点C的坐标是 ( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
11.如图,在正方形ABCD中,AB=4.若以CD为斜边向其外作等腰直角三角形DCE,连接BE,则BE的长为 ( )
A.4 B.2 C.2 D.2
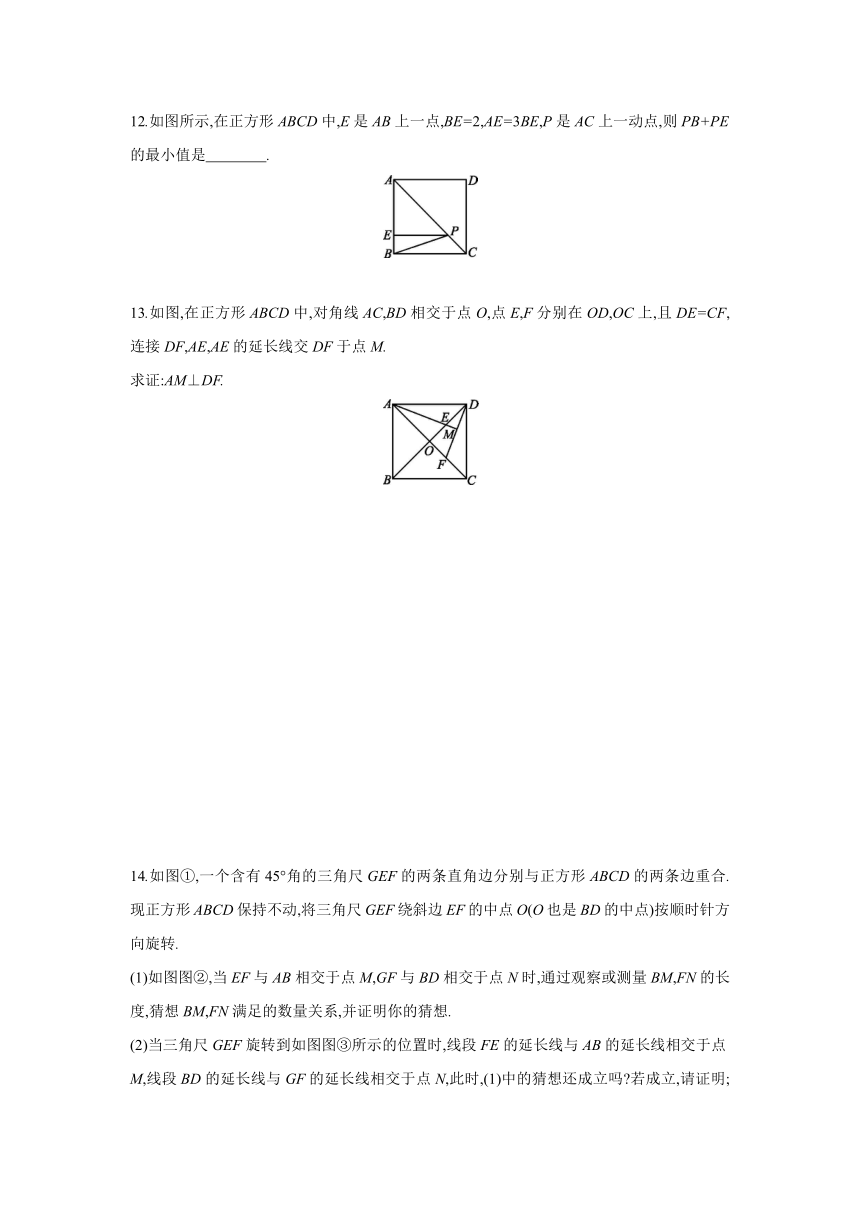
12.如图所示,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
13.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别在OD,OC上,且DE=CF,连接DF,AE,AE的延长线交DF于点M.
求证:AM⊥DF.
14.如图①,一个含有45°角的三角尺GEF的两条直角边分别与正方形ABCD的两条边重合.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(O也是BD的中点)按顺时针方向旋转.
(1)如图图②,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想.
(2)当三角尺GEF旋转到如图图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗 若成立,请证明;若不成立,请说明理由.
答案
1.2
2.-1 ∵四边形ABCD是正方形,∴AB=BC=1,∠B=∠D=90°,∴AC=.
易证△AFE≌△ADE,∴AF=AD=1,∴FC=AC-AF=-1.
3.证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°,
∴∠ABF+∠CBG=90°.
又∵BF⊥CE,∴∠BCE+∠CBG=90°,
∴∠BCE=∠ABF.
在△BCE和△ABF中,
∵∠BCE=∠ABF,BC=AB,∠CBE=∠A,
∴△BCE≌△ABF(ASA),
∴CE=BF.
4.C
5.22.5 ∵四边形ABCD是正方形,
∴∠BCD=90°.
∵BD是正方形ABCD的对角线,
∴∠DBC=45°.
又∵BE=BC,
∴∠BCE=∠BEC=×(180°-45°)=67.5°,
∴∠DCE=∠BCD-∠BCE=90°-67.5°=22.5°.
6.解:(1)证明:∵四边形ABCD是正方形,△EBC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠DCE=30°.
在△ABE和△DCE中,
∵BA=CD,∠ABE=∠DCE,BE=CE,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=×(180°-30°)=75°.
∵∠BAD=90°,∴∠EAD=90°-75°=15°,
同理可得∠ADE=15°,
∴∠AED=180°-15°-15°=150°.
7.A
8. cm2 ∵正方形ABCD的对角线相交于点O,
∴△AEO与△CFO关于点O成中心对称,
∴△AEO≌△CFO,∴S△AEO=S△CFO,
∴S△DEO+S△CFO=S△AOD.
∵对角线长为1 cm,
∴S正方形ABCD=×1×1=(cm2),
∴S△AOD= cm2,
∴阴影部分的面积为 cm2.
9.解:(1)证明:∵ 四边形ABCD是正方形,
∴AB=CB,∠A=∠C=90°.
在△ABF和△CBE中,
∵AB=CB,∠A=∠C,AF=CE,
∴△ABF≌△CBE(SAS).
(2)由已知可得正方形ABCD的面积为16,
△ABF的面积=△CBE的面积=×4×1=2,
∴四边形BEDF的面积为16-2×2=12.
10.C 如图图,连接AC.
∵四边形OABC是正方形,∴AC,OB所在直线是正方形OABC的对称轴,AC=OB=2,∴点A,C的横坐标均为1,且点A的纵坐标为1,点C的纵坐标为-1,故点C的坐标为(1,-1).故选C.
11.C 连接BD.因为四边形ABCD为正方形,所以∠BDC=45°,AD=AB=DC=4,∠A=90°.
在Rt△ABD中,由勾股定理,得BD==4.因为△DCE是等腰直角三角形,所以∠CDE=45°,所以∠BDE=∠BDC+∠CDE=90°,DE=EC==2.在Rt△BDE中,由勾股定理,得BE==2.
12.10
13.证明:∵四边形ABCD是正方形,
∴OA=OD=OC,∠AOE=∠DOF=90°.
∵DE=CF,
∴OD-DE=OC-CF,即OE=OF.
在△AOE和△DOF中,
∵OA=OD,∠AOE=∠DOF,OE=OF,
∴△AOE≌△DOF(SAS),∴∠OAE=∠ODF.
∵∠OAE+∠AEO=90°,∠AEO=∠DEM,
∴∠ODF+∠DEM=90°,
∴∠EMD=90°,即AM⊥DF.
14.解:(1)猜想:BM=FN.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,O是BD,EF的中点,BD=EF,
∴∠ABD=∠F=45°,OB=OF.
在△OBM与△OFN中,
∵∠OBM=∠F,OB=OF,∠BOM=∠FON,
∴△OBM≌△OFN(ASA),
∴BM=FN.
(2)BM=FN仍然成立.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,O是BD,EF的中点,BD=EF,
∴∠DBA=∠GFE=45°,OB=OF,
∴∠MBO=∠NFO=135°.
在△OBM与△OFN中,
∵∠MBO=∠NFO,OB=OF,∠MOB=∠NOF,
∴△OBM≌△OFN(ASA),
∴BM=FN.
知识点 1 利用正方形的性质求解与线段有关的问题
1.如图在正方形ABCD中,点E在边DC上,DE=4,EC=2,则AE的长为 .
2.如图正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,垂足为F,那么FC= .
3.如图四边形ABCD是正方形,E,F分别是AB,AD上的点,且BF⊥CE,垂足为G.求证:CE=BF.
知识点 2 利用正方形的性质求解与角有关的问题
4.如图在正方形ABCD的外侧作等边三角形ADE,则∠AEB的度数为 ( )
A.10° B.12.5° C.15° D.20°
5.如图E为正方形ABCD的对角线BD上的一点,且BE=BC,则∠DCE= °.
6.[教材习题1.7第2题变式题] 如图四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
知识点 3 利用正方形的性质求解与面积有关的问题
7.若正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
8.[2020·肥城期末] 如图正方形ABCD的对角线相交于点O,对角线长为1 cm,过点O任作一条直线分别交AD,BC于点E,F,则阴影部分的面积是 .
9.如图在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.
(1)求证:△ABF≌△CBE;
(2)若AB=4,AF=1,求四边形BEDF的面积.
知识点 4 正方形对称性的应用
10.如图在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(2,0),则顶点C的坐标是 ( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
11.如图,在正方形ABCD中,AB=4.若以CD为斜边向其外作等腰直角三角形DCE,连接BE,则BE的长为 ( )
A.4 B.2 C.2 D.2
12.如图所示,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
13.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别在OD,OC上,且DE=CF,连接DF,AE,AE的延长线交DF于点M.
求证:AM⊥DF.
14.如图①,一个含有45°角的三角尺GEF的两条直角边分别与正方形ABCD的两条边重合.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(O也是BD的中点)按顺时针方向旋转.
(1)如图图②,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想.
(2)当三角尺GEF旋转到如图图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗 若成立,请证明;若不成立,请说明理由.
答案
1.2
2.-1 ∵四边形ABCD是正方形,∴AB=BC=1,∠B=∠D=90°,∴AC=.
易证△AFE≌△ADE,∴AF=AD=1,∴FC=AC-AF=-1.
3.证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°,
∴∠ABF+∠CBG=90°.
又∵BF⊥CE,∴∠BCE+∠CBG=90°,
∴∠BCE=∠ABF.
在△BCE和△ABF中,
∵∠BCE=∠ABF,BC=AB,∠CBE=∠A,
∴△BCE≌△ABF(ASA),
∴CE=BF.
4.C
5.22.5 ∵四边形ABCD是正方形,
∴∠BCD=90°.
∵BD是正方形ABCD的对角线,
∴∠DBC=45°.
又∵BE=BC,
∴∠BCE=∠BEC=×(180°-45°)=67.5°,
∴∠DCE=∠BCD-∠BCE=90°-67.5°=22.5°.
6.解:(1)证明:∵四边形ABCD是正方形,△EBC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠DCE=30°.
在△ABE和△DCE中,
∵BA=CD,∠ABE=∠DCE,BE=CE,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=×(180°-30°)=75°.
∵∠BAD=90°,∴∠EAD=90°-75°=15°,
同理可得∠ADE=15°,
∴∠AED=180°-15°-15°=150°.
7.A
8. cm2 ∵正方形ABCD的对角线相交于点O,
∴△AEO与△CFO关于点O成中心对称,
∴△AEO≌△CFO,∴S△AEO=S△CFO,
∴S△DEO+S△CFO=S△AOD.
∵对角线长为1 cm,
∴S正方形ABCD=×1×1=(cm2),
∴S△AOD= cm2,
∴阴影部分的面积为 cm2.
9.解:(1)证明:∵ 四边形ABCD是正方形,
∴AB=CB,∠A=∠C=90°.
在△ABF和△CBE中,
∵AB=CB,∠A=∠C,AF=CE,
∴△ABF≌△CBE(SAS).
(2)由已知可得正方形ABCD的面积为16,
△ABF的面积=△CBE的面积=×4×1=2,
∴四边形BEDF的面积为16-2×2=12.
10.C 如图图,连接AC.
∵四边形OABC是正方形,∴AC,OB所在直线是正方形OABC的对称轴,AC=OB=2,∴点A,C的横坐标均为1,且点A的纵坐标为1,点C的纵坐标为-1,故点C的坐标为(1,-1).故选C.
11.C 连接BD.因为四边形ABCD为正方形,所以∠BDC=45°,AD=AB=DC=4,∠A=90°.
在Rt△ABD中,由勾股定理,得BD==4.因为△DCE是等腰直角三角形,所以∠CDE=45°,所以∠BDE=∠BDC+∠CDE=90°,DE=EC==2.在Rt△BDE中,由勾股定理,得BE==2.
12.10
13.证明:∵四边形ABCD是正方形,
∴OA=OD=OC,∠AOE=∠DOF=90°.
∵DE=CF,
∴OD-DE=OC-CF,即OE=OF.
在△AOE和△DOF中,
∵OA=OD,∠AOE=∠DOF,OE=OF,
∴△AOE≌△DOF(SAS),∴∠OAE=∠ODF.
∵∠OAE+∠AEO=90°,∠AEO=∠DEM,
∴∠ODF+∠DEM=90°,
∴∠EMD=90°,即AM⊥DF.
14.解:(1)猜想:BM=FN.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,O是BD,EF的中点,BD=EF,
∴∠ABD=∠F=45°,OB=OF.
在△OBM与△OFN中,
∵∠OBM=∠F,OB=OF,∠BOM=∠FON,
∴△OBM≌△OFN(ASA),
∴BM=FN.
(2)BM=FN仍然成立.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,O是BD,EF的中点,BD=EF,
∴∠DBA=∠GFE=45°,OB=OF,
∴∠MBO=∠NFO=135°.
在△OBM与△OFN中,
∵∠MBO=∠NFO,OB=OF,∠MOB=∠NOF,
∴△OBM≌△OFN(ASA),
∴BM=FN.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
