北师大版数学九年级上册同步课时练习:1.3 第2课时 正方形的判定 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:1.3 第2课时 正方形的判定 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 06:56:24 | ||
图片预览



文档简介
第2课时 正方形的判定
知识点 1 用定义判定正方形
1.如图,如图果要证明 ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明 ( )
A.AB=BD且AC⊥BD B.∠BAD=90°且AB=AD
C.∠BAD=90°且AC=BD D.AC和BD互相垂直平分
2.已知在四边形ABCD中,AB CD,∠C=90°,若使四边形ABCD是正方形,则还需加上一个条件: (填一个即可).
知识点 2 利用菱形判定四边形是正方形
3.如图,在菱形ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是( )
A.BD=AB B.AC=AD C.∠ABC=90° D.OD=AC
4.[教材习题1.8第3题变式题] 如图,有4个动点P,Q,E,F分别从正方形ABCD的4个顶点A,B,C,D同时出发,沿着AB,BC,CD,DA以同样的速度向点B,C,D,A移动.请判断四边形PQEF的形状.
知识点 3 利用矩形判定四边形是正方形
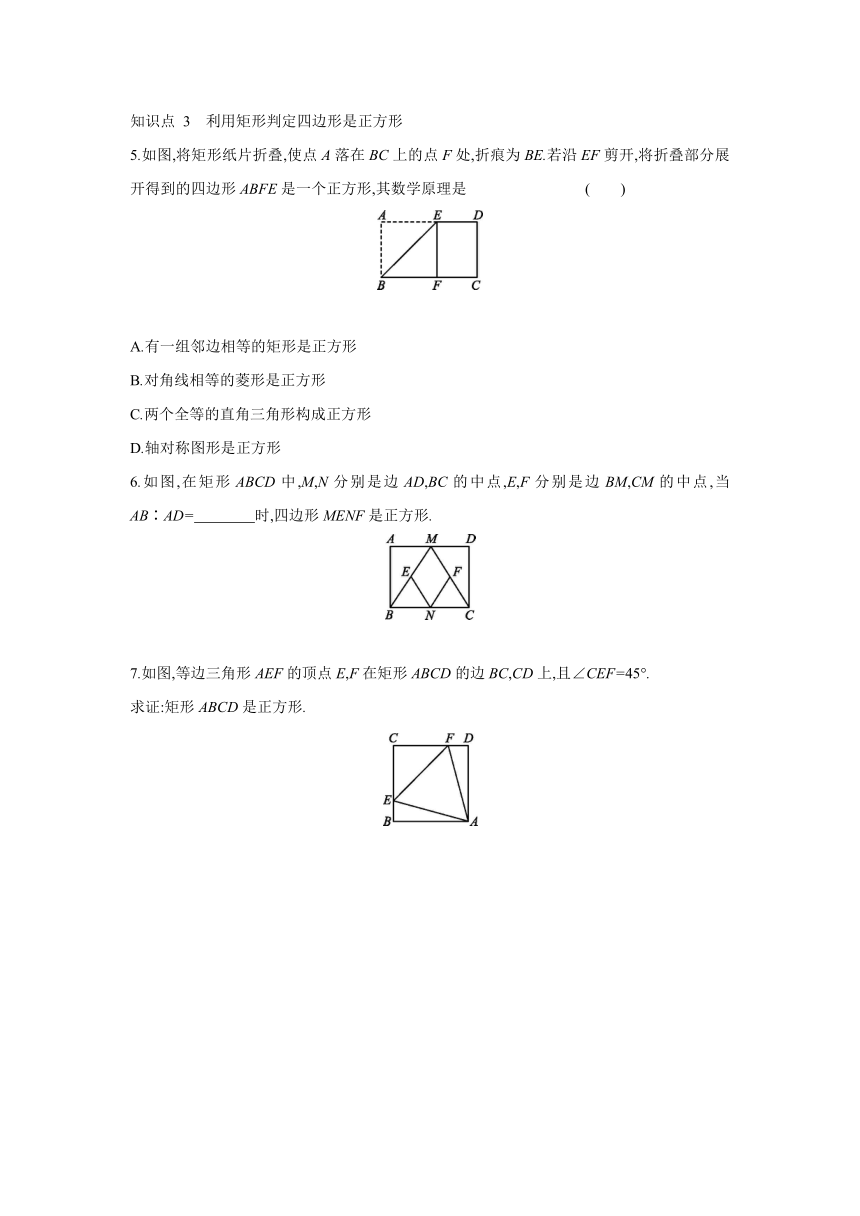
5.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE.若沿EF剪开,将折叠部分展开得到的四边形ABFE是一个正方形,其数学原理是 ( )
A.有一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
6.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB∶AD= 时,四边形MENF是正方形.
7.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
8.若顺次连接四边形ABCD各边中点所得的四边形是正方形,则四边形ABCD一定是 ( )
A.矩形 B.对角线互相垂直的四边形
C.菱形 D.对角线互相垂直且相等的四边形
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加下列条件后,仍不能判定四边形ECFB为正方形的是 ( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
10.如图所示,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
11.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
12.如图,在△ABC中,D为BC边上的一动点(点D不与B,C两点重合),连接AD,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试探索当AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(2)在(1)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形 为什么
13.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的AD或CD边的夹角是30°时,直接写出∠EFC的度数.
答案
1.B
2.AB=BC(答案不唯一)
3.C 要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角;(2)对角线相等.即∠ABC=90°或AC=BD等.故选C.
4.解:由题意知AP=BQ=CE=DF.
在正方形ABCD中,AB=BC=CD=DA,
∴AF=BP=CQ=DE.
又∵∠A=∠B=∠C=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF,
∴FP=PQ=QE=EF,
∴四边形PQEF是菱形.
∵△AFP≌△BPQ,
∴∠APF=∠BQP,
∴∠BPQ+∠APF=∠BPQ+∠BQP=90°,
∴∠FPQ=90°,
∴四边形PQEF为正方形.
5.A ∵△BEF是由△BEA折叠得到的,
∴∠EFB=∠A=90°,BA=BF.又∵∠ABF=90°,∴四边形ABFE是矩形.又∵BA=BF,∴四边形ABFE是正方形.
6.1∶2 当AB∶AD=1∶2时,四边形MENF是正方形.
理由:∵F为CM的中点,N为BC的中点,E为BM的中点,∴NF EM,∴四边形MENF是平行四边形.∵AB∶AD=1∶2,AM=DM,AB=DC,
∴AB=AM=DM=CD.
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°.
∴四边形MENF是矩形.
易得△ABM≌△DCM,∴BM=CM.
∵E,F分别是BM,CM的中点,
∴ME=MF,
∴四边形MENF是正方形,
即当AB∶AD=1∶2时,四边形MENF是正方形.
故答案为1∶2.
7.证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,
∴∠CFE=180°-∠C-∠CEF=45°,
从而∠AFD=∠AEB=180°-45°-60°=75°,
∴△ABE≌△ADF(AAS),
∴AB=AD,∴矩形ABCD是正方形.
8.D 9.D
10.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC.
又∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴ ABCD是菱形.
(2)∵∠ADB=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠ADB=∠DAC,∴AO=DO.
由(1)知四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,
∴菱形ABCD是正方形.
11.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵BA=BC,BD=BD,
∴△ABD≌△CBD,
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN,
∴矩形MPND是正方形.
12.解:(1)当AD平分∠BAC时,四边形AEDF为菱形.
理由:∵AE∥DF,DE∥AF,
∴四边形AEDF为平行四边形.
∵AD平分∠BAC,
∴∠EAD=∠FAD.
∵DE∥AF,
∴∠FAD=∠ADE,
∴∠EAD=∠ADE,
∴AE=DE,
∴ AEDF为菱形.
(2)当∠BAC=90°时,菱形AEDF是正方形.理由:因为有一个角是直角的菱形是正方形.
13.解:(1)证明:如图图①,过点E作EP⊥CD于点P,EQ⊥BC于点Q,则∠EPC=∠EQC=90°.
∵四边形ABCD为正方形,
∴∠BCD=90°,∠DCA=∠BCA,
∴∠QEP=90°,EQ=EP.
∴∠QEF+∠PEF=90°.
∵四边形DEFG为矩形,
∴∠DEF=90°,∴∠PED+∠PEF=90°,
∴∠QEF=∠PED.
在△EQF和△EPD中,
∵∠QEF=∠PED,EQ=EP,∠EQF=∠EPD,
∴△EQF≌△EPD,
∴EF=ED,
∴矩形DEFG是正方形.
(2)在△ABC中,易得AC=AB=2.
∵CE=,
∴AE=CE,易得DE⊥AC,
∴点F与点C重合.
如图图②.
此时易得△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与CD的夹角为30°时,∠EFC=30°.
知识点 1 用定义判定正方形
1.如图,如图果要证明 ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明 ( )
A.AB=BD且AC⊥BD B.∠BAD=90°且AB=AD
C.∠BAD=90°且AC=BD D.AC和BD互相垂直平分
2.已知在四边形ABCD中,AB CD,∠C=90°,若使四边形ABCD是正方形,则还需加上一个条件: (填一个即可).
知识点 2 利用菱形判定四边形是正方形
3.如图,在菱形ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是( )
A.BD=AB B.AC=AD C.∠ABC=90° D.OD=AC
4.[教材习题1.8第3题变式题] 如图,有4个动点P,Q,E,F分别从正方形ABCD的4个顶点A,B,C,D同时出发,沿着AB,BC,CD,DA以同样的速度向点B,C,D,A移动.请判断四边形PQEF的形状.
知识点 3 利用矩形判定四边形是正方形
5.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE.若沿EF剪开,将折叠部分展开得到的四边形ABFE是一个正方形,其数学原理是 ( )
A.有一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
6.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB∶AD= 时,四边形MENF是正方形.
7.如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
8.若顺次连接四边形ABCD各边中点所得的四边形是正方形,则四边形ABCD一定是 ( )
A.矩形 B.对角线互相垂直的四边形
C.菱形 D.对角线互相垂直且相等的四边形
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加下列条件后,仍不能判定四边形ECFB为正方形的是 ( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
10.如图所示,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
11.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
12.如图,在△ABC中,D为BC边上的一动点(点D不与B,C两点重合),连接AD,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试探索当AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(2)在(1)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形 为什么
13.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的AD或CD边的夹角是30°时,直接写出∠EFC的度数.
答案
1.B
2.AB=BC(答案不唯一)
3.C 要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角;(2)对角线相等.即∠ABC=90°或AC=BD等.故选C.
4.解:由题意知AP=BQ=CE=DF.
在正方形ABCD中,AB=BC=CD=DA,
∴AF=BP=CQ=DE.
又∵∠A=∠B=∠C=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF,
∴FP=PQ=QE=EF,
∴四边形PQEF是菱形.
∵△AFP≌△BPQ,
∴∠APF=∠BQP,
∴∠BPQ+∠APF=∠BPQ+∠BQP=90°,
∴∠FPQ=90°,
∴四边形PQEF为正方形.
5.A ∵△BEF是由△BEA折叠得到的,
∴∠EFB=∠A=90°,BA=BF.又∵∠ABF=90°,∴四边形ABFE是矩形.又∵BA=BF,∴四边形ABFE是正方形.
6.1∶2 当AB∶AD=1∶2时,四边形MENF是正方形.
理由:∵F为CM的中点,N为BC的中点,E为BM的中点,∴NF EM,∴四边形MENF是平行四边形.∵AB∶AD=1∶2,AM=DM,AB=DC,
∴AB=AM=DM=CD.
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°.
∴四边形MENF是矩形.
易得△ABM≌△DCM,∴BM=CM.
∵E,F分别是BM,CM的中点,
∴ME=MF,
∴四边形MENF是正方形,
即当AB∶AD=1∶2时,四边形MENF是正方形.
故答案为1∶2.
7.证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,
∴∠CFE=180°-∠C-∠CEF=45°,
从而∠AFD=∠AEB=180°-45°-60°=75°,
∴△ABE≌△ADF(AAS),
∴AB=AD,∴矩形ABCD是正方形.
8.D 9.D
10.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC.
又∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴ ABCD是菱形.
(2)∵∠ADB=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠ADB=∠DAC,∴AO=DO.
由(1)知四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,
∴菱形ABCD是正方形.
11.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵BA=BC,BD=BD,
∴△ABD≌△CBD,
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN,
∴矩形MPND是正方形.
12.解:(1)当AD平分∠BAC时,四边形AEDF为菱形.
理由:∵AE∥DF,DE∥AF,
∴四边形AEDF为平行四边形.
∵AD平分∠BAC,
∴∠EAD=∠FAD.
∵DE∥AF,
∴∠FAD=∠ADE,
∴∠EAD=∠ADE,
∴AE=DE,
∴ AEDF为菱形.
(2)当∠BAC=90°时,菱形AEDF是正方形.理由:因为有一个角是直角的菱形是正方形.
13.解:(1)证明:如图图①,过点E作EP⊥CD于点P,EQ⊥BC于点Q,则∠EPC=∠EQC=90°.
∵四边形ABCD为正方形,
∴∠BCD=90°,∠DCA=∠BCA,
∴∠QEP=90°,EQ=EP.
∴∠QEF+∠PEF=90°.
∵四边形DEFG为矩形,
∴∠DEF=90°,∴∠PED+∠PEF=90°,
∴∠QEF=∠PED.
在△EQF和△EPD中,
∵∠QEF=∠PED,EQ=EP,∠EQF=∠EPD,
∴△EQF≌△EPD,
∴EF=ED,
∴矩形DEFG是正方形.
(2)在△ABC中,易得AC=AB=2.
∵CE=,
∴AE=CE,易得DE⊥AC,
∴点F与点C重合.
如图图②.
此时易得△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与CD的夹角为30°时,∠EFC=30°.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
