北师大版数学九年级上册同步课时练习:3.1 第3课时 利用概率玩转盘游戏 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:3.1 第3课时 利用概率玩转盘游戏 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 200.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览


文档简介
第3课时 利用概率玩转盘游戏
知识点 概率在游戏中的应用
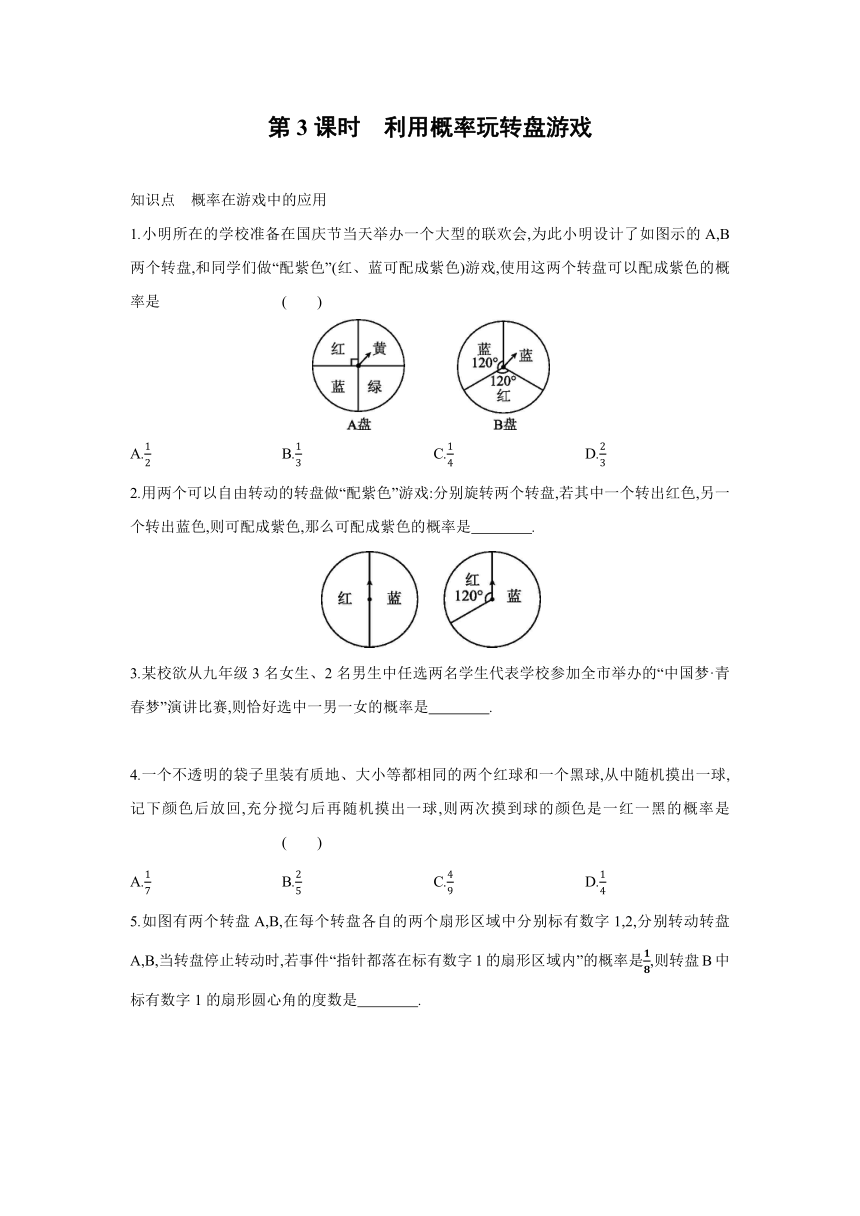
1.小明所在的学校准备在国庆节当天举办一个大型的联欢会,为此小明设计了如图示的A,B两个转盘,和同学们做“配紫色”(红、蓝可配成紫色)游戏,使用这两个转盘可以配成紫色的概率是 ( )
A. B. C. D.
2.用两个可以自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色,则可配成紫色,那么可配成紫色的概率是 .
3.某校欲从九年级3名女生、2名男生中任选两名学生代表学校参加全市举办的“中国梦·青春梦”演讲比赛,则恰好选中一男一女的概率是 .
4.一个不透明的袋子里装有质地、大小等都相同的两个红球和一个黑球,从中随机摸出一球,记下颜色后放回,充分搅匀后再随机摸出一球,则两次摸到球的颜色是一红一黑的概率是 ( )
A. B. C. D.
5.如图有两个转盘A,B,在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘A,B,当转盘停止转动时,若事件“指针都落在标有数字1的扇形区域内”的概率是,则转盘B中标有数字1的扇形圆心角的度数是 .
6.在一次数学兴趣小组活动中,李燕和刘凯两名同学设计了如图示的甲、乙两个转盘做游戏.游戏规则如图下:两人同时转动甲、乙两转盘,转盘停止后,若指针所指区域内两数和小于11,则李燕获胜;若指针所指区域内两数和等于11,则为平局;若指针所指区域内两数和大于11,则刘凯获胜(若指针停在等分线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能结果;
(2)分别求出李燕和刘凯获胜的概率.
答案
1.C
2. 将第二个转盘中的蓝色区域平均分成两份,分别记为蓝1,蓝2,可画树状图如图下:
共有6种等可能的结果,其中一个为红色,另一个为蓝色的结果有3种,所以可配成紫色的概率为=.
3. (解法1)列表如图下:
女 女 女 男 男
女 (女,女) (女,女) (女,男) (女,男)
女 (女,女) (女,女) (女,男) (女,男)
女 (女,女) (女,女) (女,男) (女,男)
男 (男,女) (男,女) (男,女) (男,男)
男 (男,女) (男,女) (男,女) (男,男)
所有等可能的结果数为20,选中一男一女的结果数为12,
所以,选中一男一女的概率P==.
(解法2)画树状图如图下:
所有可能的结果数为20,选中一男一女的结果数为12,
所以,选中一男一女的概率P==.
4.C 画树状图如图下:
因为共有9种等可能的结果,其中两次摸到球的颜色是一红一黑的结果有4种,
所以两次摸到球的颜色是一红一黑的概率是.
故选C.
5.90°
6.解:(1)将乙转盘中数字6所在区域平均分成两份,记为6A,6B,列表如图下:
乙 和 甲 6A 6B 7 8
3 9 9 10 11
4 10 10 11 12
5 11 11 12 13
所有等可能的结果共有12种.
(2)由(1)可知,和小于11的结果有5种,和大于11的结果有3种,所以李燕获胜的概率为,刘凯获胜的概率为=.
知识点 概率在游戏中的应用
1.小明所在的学校准备在国庆节当天举办一个大型的联欢会,为此小明设计了如图示的A,B两个转盘,和同学们做“配紫色”(红、蓝可配成紫色)游戏,使用这两个转盘可以配成紫色的概率是 ( )
A. B. C. D.
2.用两个可以自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色,则可配成紫色,那么可配成紫色的概率是 .
3.某校欲从九年级3名女生、2名男生中任选两名学生代表学校参加全市举办的“中国梦·青春梦”演讲比赛,则恰好选中一男一女的概率是 .
4.一个不透明的袋子里装有质地、大小等都相同的两个红球和一个黑球,从中随机摸出一球,记下颜色后放回,充分搅匀后再随机摸出一球,则两次摸到球的颜色是一红一黑的概率是 ( )
A. B. C. D.
5.如图有两个转盘A,B,在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘A,B,当转盘停止转动时,若事件“指针都落在标有数字1的扇形区域内”的概率是,则转盘B中标有数字1的扇形圆心角的度数是 .
6.在一次数学兴趣小组活动中,李燕和刘凯两名同学设计了如图示的甲、乙两个转盘做游戏.游戏规则如图下:两人同时转动甲、乙两转盘,转盘停止后,若指针所指区域内两数和小于11,则李燕获胜;若指针所指区域内两数和等于11,则为平局;若指针所指区域内两数和大于11,则刘凯获胜(若指针停在等分线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能结果;
(2)分别求出李燕和刘凯获胜的概率.
答案
1.C
2. 将第二个转盘中的蓝色区域平均分成两份,分别记为蓝1,蓝2,可画树状图如图下:
共有6种等可能的结果,其中一个为红色,另一个为蓝色的结果有3种,所以可配成紫色的概率为=.
3. (解法1)列表如图下:
女 女 女 男 男
女 (女,女) (女,女) (女,男) (女,男)
女 (女,女) (女,女) (女,男) (女,男)
女 (女,女) (女,女) (女,男) (女,男)
男 (男,女) (男,女) (男,女) (男,男)
男 (男,女) (男,女) (男,女) (男,男)
所有等可能的结果数为20,选中一男一女的结果数为12,
所以,选中一男一女的概率P==.
(解法2)画树状图如图下:
所有可能的结果数为20,选中一男一女的结果数为12,
所以,选中一男一女的概率P==.
4.C 画树状图如图下:
因为共有9种等可能的结果,其中两次摸到球的颜色是一红一黑的结果有4种,
所以两次摸到球的颜色是一红一黑的概率是.
故选C.
5.90°
6.解:(1)将乙转盘中数字6所在区域平均分成两份,记为6A,6B,列表如图下:
乙 和 甲 6A 6B 7 8
3 9 9 10 11
4 10 10 11 12
5 11 11 12 13
所有等可能的结果共有12种.
(2)由(1)可知,和小于11的结果有5种,和大于11的结果有3种,所以李燕获胜的概率为,刘凯获胜的概率为=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
