北师大版数学九年级上册同步课时练习:4.3 相似多边形 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:4.3 相似多边形 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 218.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览



文档简介
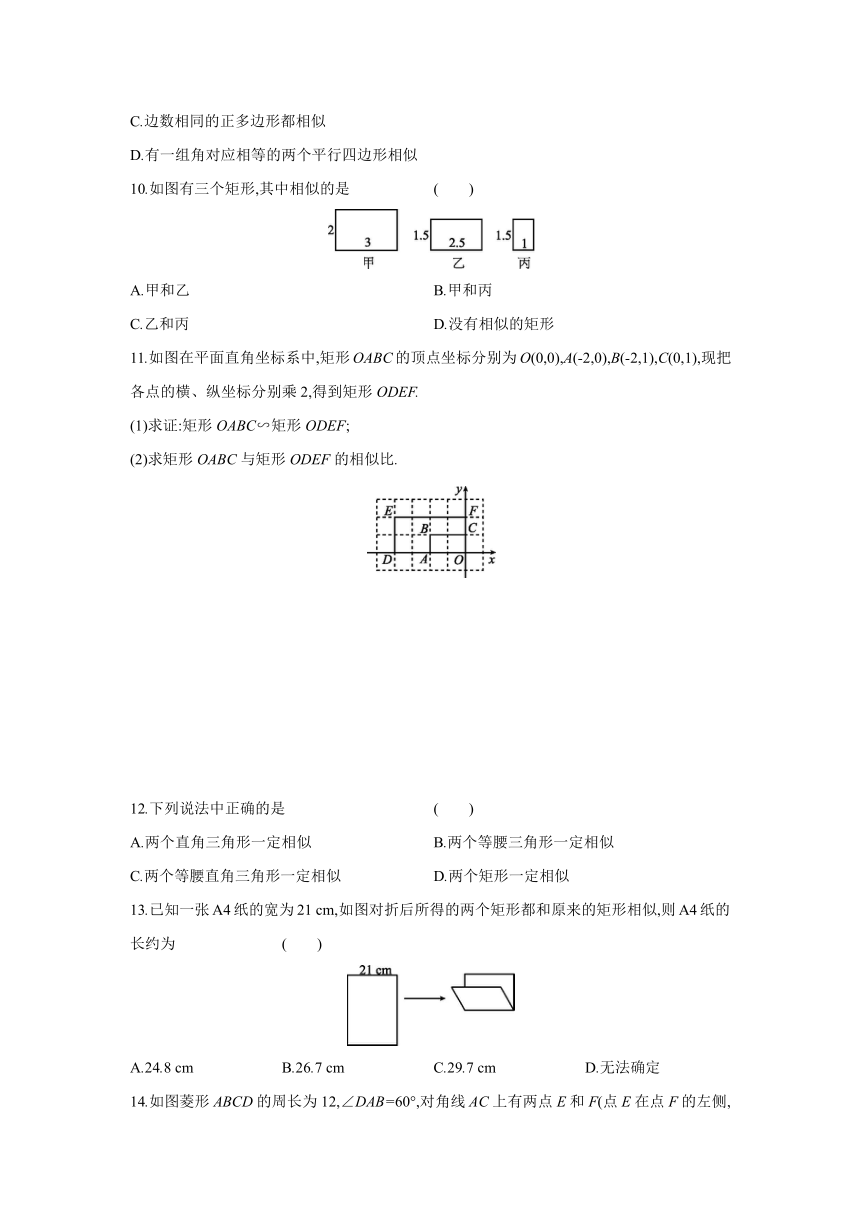
3 相似多边形
知识点 1 相似多边形的定义及性质
1.观察下列各组图形,其中是相似图形的是 ( )
2.下列说法中错误的是 ( )
A.相似多边形的对应边成比例
B.相似多边形的对应角相等
C.相似多边形的边数相同
D.对应边成比例的两个多边形是相似多边形
3.如图示的两个四边形相似,则∠α的度数是 ( )
A.60° B.75° C.87° D.120°
4.一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边的长为24,则这个多边形的最短边的长为 ( )
A.6 B.8 C.12 D.10
5.如图示,正五边形FGHMN∽正五边形ABCDE,若AB∶FG=2∶3,则下列结论正确的是 ( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
6.如图在矩形ABCD中,AB=4,M,N分别是AD,BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为 .
7.如图四边形ABCD∽四边形A'B'C'D'.
(1)α的度数为多少 它们的相似比是多少
(2)求边x,y的长度.
8.已知四边形ABCD与四边形A1B1C1D1相似,并且点A与点A1、点B与点B1、点C与点C1、点D与点D1对应.
(1)已知∠A=40°,∠B=110°,∠C1=90°,求∠D的度数;
(2)已知AB=9,CD=15,A1B1=6,A1D1=4,B1C1=8,求四边形ABCD的周长.
知识点 2 相似多边形的判定
9.下列判断正确的是 ( )
A.两个对应角相等的多边形相似
B.两个对应边成比例的多边形相似
C.边数相同的正多边形都相似
D.有一组角对应相等的两个平行四边形相似
10.如图有三个矩形,其中相似的是 ( )
A.甲和乙 B.甲和丙
C.乙和丙 D.没有相似的矩形
11.如图在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(-2,0),B(-2,1),C(0,1),现把各点的横、纵坐标分别乘2,得到矩形ODEF.
(1)求证:矩形OABC∽矩形ODEF;
(2)求矩形OABC与矩形ODEF的相似比.
12.下列说法中正确的是 ( )
A.两个直角三角形一定相似 B.两个等腰三角形一定相似
C.两个等腰直角三角形一定相似 D.两个矩形一定相似
13.已知一张A4纸的宽为21 cm,如图对折后所得的两个矩形都和原来的矩形相似,则A4纸的长约为 ( )
A.24.8 cm B.26.7 cm C.29.7 cm D.无法确定
14.如图菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧,且不与点A,C重合),若要使四边形DEBF与菱形ABCD相似,则AE的长为 .
15.定义:四边形的一条对角线把这个四边形分成两个三角形,如图果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线.如图,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC= °.
16.如图,在四边形ABCD中,EF∥AB∥DC,AB=9,DC=4,若用EF把原四边形分成两个相似的小四边形,求EF的长.
17.一个矩形ABCD的较短边长为2.
(1)如图①,将矩形ABCD沿它的长边对折(MN为折痕),得到的矩形与原矩形相似,求矩形ABCD的较长边长;
(2)如图②,已知矩形ABCD的较长边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
答案
1.D A项,两图形形状不同,故不是相似图形;B项,两图形形状不同,故不是相似图形;C项,两图形形状不同,故不是相似图形;D项,两图形形状相同,故是相似图形.故选D.
2.D
3.C 根据相似多边形的特点可知对应角相等,所以∠α=360°-60°-138°-75°=87°.故选C.
4.B 设这个多边形的最短边的长为x.∵两个多边形相似,∴24∶6=x∶2,解得x=8.故选B.
5.B ∵正五边形FGHMN∽正五边形ABCDE,∴两个正五边形的对应边成比例,对应角相等,∴DE∶MN=AB∶FG=2∶3,∠A=∠F,∴3DE=2MN.故选B.
6.4 由已知得MN=AB,DM=AD=BC.又∵矩形DMNC与矩形ABCD相似,∴=,即AD2=AB2.再由AB=4,得AD=4.
7.解:(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠A'=∠A=62°,∠B'=∠B=75°,
∴α=360°-62°-75°-140°=83°.
它们的相似比为=.
(2)∵四边形ABCD∽四边形A'B'C'D',
∴==,解得x=12,y=.
8.解:(1)∵四边形ABCD∽四边形A1B1C1D1,
∴∠C=∠C1=90°,
∴∠D=360°-∠A-∠B-∠C=360°-40°-110°-90°=120°.
(2)∵四边形ABCD∽四边形A1B1C1D1,
∴==,
∴==,
∴BC=12,AD=6,
∴四边形ABCD的周长=AB+BC+CD+AD=9+12+15+6=42.
9.C
10.B 三个矩形的角都是直角,甲、乙、丙短边与长边的比分别为2∶3,1.5∶2.5=3∶5,1∶1.5=2∶3,∴甲和丙相似.故选B.
11.解:(1)证明:由题意得D(-4,0),E(-4,2),F(0,2),
∴OA=2,AB=1,BC=2,OC=1,OD=4,DE=2,EF=4,OF=2,
∴OA∶OD=AB∶DE=BC∶EF=OC∶OF=1∶2.
又∵矩形OABC与矩形ODEF的角都是直角,
∴矩形OABC∽矩形ODEF.
(2)∵OA∶OD=1∶2,
∴矩形OABC与矩形ODEF的相似比为1∶2.
12.C 13.C
14. 如图图,连接BD交AC于点O.
∵四边形ABCD是菱形,周长为12,∴AB=BC=CD=AD=3,BD⊥AC.∵∠DAB=60°,∴∠DAO=∠DAB=30°,∴OD=AD=.由勾股定理可得AO=.∵四边形DEBF与菱形ABCD相似,∴∠EDF=∠DAB=60°,∴∠EDO=∠EDF=30°,∴DE=2OE.又∵∠DAO=30°,∠DEO=60°,∴∠DAO=∠ADE=30°,∴AE=DE=2OE,∴AO=3OE,∴OE=,∴AE=2OE=.
15.145 ∵∠ABC=70°,BD平分∠ABC,∴∠ABD=∠DBC.
又∵对角线BD是它的相似对角线,
∴△ABD∽△DBC,
∴∠A=∠BDC,∠ADB=∠C,
∴∠A+∠C=∠ADC.
又∵∠A+∠C+∠ADC=360°-70°=290°,
∴∠ADC=145°.
16.解:由题意,得四边形DEFC∽四边形EABF,
则=,
即EF2=DC·AB=4×9=36,∴EF=6.
17.解:(1)由已知得MN=AB=2,DM=AD=BC.
∵将矩形ABCD沿MN对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,
∴=,
∴DM·BC=AB·MN,即BC2=4,
∴BC=2,即矩形ABCD的较长边长为2.
(2)∵余下的矩形EFDC与原矩形ABCD相似,
∴=.
∵AB=CD=2,BC=4,∴DF==1,
∴余下的矩形EFDC的面积=CD·DF=2×1=2.
知识点 1 相似多边形的定义及性质
1.观察下列各组图形,其中是相似图形的是 ( )
2.下列说法中错误的是 ( )
A.相似多边形的对应边成比例
B.相似多边形的对应角相等
C.相似多边形的边数相同
D.对应边成比例的两个多边形是相似多边形
3.如图示的两个四边形相似,则∠α的度数是 ( )
A.60° B.75° C.87° D.120°
4.一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边的长为24,则这个多边形的最短边的长为 ( )
A.6 B.8 C.12 D.10
5.如图示,正五边形FGHMN∽正五边形ABCDE,若AB∶FG=2∶3,则下列结论正确的是 ( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
6.如图在矩形ABCD中,AB=4,M,N分别是AD,BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为 .
7.如图四边形ABCD∽四边形A'B'C'D'.
(1)α的度数为多少 它们的相似比是多少
(2)求边x,y的长度.
8.已知四边形ABCD与四边形A1B1C1D1相似,并且点A与点A1、点B与点B1、点C与点C1、点D与点D1对应.
(1)已知∠A=40°,∠B=110°,∠C1=90°,求∠D的度数;
(2)已知AB=9,CD=15,A1B1=6,A1D1=4,B1C1=8,求四边形ABCD的周长.
知识点 2 相似多边形的判定
9.下列判断正确的是 ( )
A.两个对应角相等的多边形相似
B.两个对应边成比例的多边形相似
C.边数相同的正多边形都相似
D.有一组角对应相等的两个平行四边形相似
10.如图有三个矩形,其中相似的是 ( )
A.甲和乙 B.甲和丙
C.乙和丙 D.没有相似的矩形
11.如图在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(-2,0),B(-2,1),C(0,1),现把各点的横、纵坐标分别乘2,得到矩形ODEF.
(1)求证:矩形OABC∽矩形ODEF;
(2)求矩形OABC与矩形ODEF的相似比.
12.下列说法中正确的是 ( )
A.两个直角三角形一定相似 B.两个等腰三角形一定相似
C.两个等腰直角三角形一定相似 D.两个矩形一定相似
13.已知一张A4纸的宽为21 cm,如图对折后所得的两个矩形都和原来的矩形相似,则A4纸的长约为 ( )
A.24.8 cm B.26.7 cm C.29.7 cm D.无法确定
14.如图菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧,且不与点A,C重合),若要使四边形DEBF与菱形ABCD相似,则AE的长为 .
15.定义:四边形的一条对角线把这个四边形分成两个三角形,如图果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线.如图,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC= °.
16.如图,在四边形ABCD中,EF∥AB∥DC,AB=9,DC=4,若用EF把原四边形分成两个相似的小四边形,求EF的长.
17.一个矩形ABCD的较短边长为2.
(1)如图①,将矩形ABCD沿它的长边对折(MN为折痕),得到的矩形与原矩形相似,求矩形ABCD的较长边长;
(2)如图②,已知矩形ABCD的较长边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
答案
1.D A项,两图形形状不同,故不是相似图形;B项,两图形形状不同,故不是相似图形;C项,两图形形状不同,故不是相似图形;D项,两图形形状相同,故是相似图形.故选D.
2.D
3.C 根据相似多边形的特点可知对应角相等,所以∠α=360°-60°-138°-75°=87°.故选C.
4.B 设这个多边形的最短边的长为x.∵两个多边形相似,∴24∶6=x∶2,解得x=8.故选B.
5.B ∵正五边形FGHMN∽正五边形ABCDE,∴两个正五边形的对应边成比例,对应角相等,∴DE∶MN=AB∶FG=2∶3,∠A=∠F,∴3DE=2MN.故选B.
6.4 由已知得MN=AB,DM=AD=BC.又∵矩形DMNC与矩形ABCD相似,∴=,即AD2=AB2.再由AB=4,得AD=4.
7.解:(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠A'=∠A=62°,∠B'=∠B=75°,
∴α=360°-62°-75°-140°=83°.
它们的相似比为=.
(2)∵四边形ABCD∽四边形A'B'C'D',
∴==,解得x=12,y=.
8.解:(1)∵四边形ABCD∽四边形A1B1C1D1,
∴∠C=∠C1=90°,
∴∠D=360°-∠A-∠B-∠C=360°-40°-110°-90°=120°.
(2)∵四边形ABCD∽四边形A1B1C1D1,
∴==,
∴==,
∴BC=12,AD=6,
∴四边形ABCD的周长=AB+BC+CD+AD=9+12+15+6=42.
9.C
10.B 三个矩形的角都是直角,甲、乙、丙短边与长边的比分别为2∶3,1.5∶2.5=3∶5,1∶1.5=2∶3,∴甲和丙相似.故选B.
11.解:(1)证明:由题意得D(-4,0),E(-4,2),F(0,2),
∴OA=2,AB=1,BC=2,OC=1,OD=4,DE=2,EF=4,OF=2,
∴OA∶OD=AB∶DE=BC∶EF=OC∶OF=1∶2.
又∵矩形OABC与矩形ODEF的角都是直角,
∴矩形OABC∽矩形ODEF.
(2)∵OA∶OD=1∶2,
∴矩形OABC与矩形ODEF的相似比为1∶2.
12.C 13.C
14. 如图图,连接BD交AC于点O.
∵四边形ABCD是菱形,周长为12,∴AB=BC=CD=AD=3,BD⊥AC.∵∠DAB=60°,∴∠DAO=∠DAB=30°,∴OD=AD=.由勾股定理可得AO=.∵四边形DEBF与菱形ABCD相似,∴∠EDF=∠DAB=60°,∴∠EDO=∠EDF=30°,∴DE=2OE.又∵∠DAO=30°,∠DEO=60°,∴∠DAO=∠ADE=30°,∴AE=DE=2OE,∴AO=3OE,∴OE=,∴AE=2OE=.
15.145 ∵∠ABC=70°,BD平分∠ABC,∴∠ABD=∠DBC.
又∵对角线BD是它的相似对角线,
∴△ABD∽△DBC,
∴∠A=∠BDC,∠ADB=∠C,
∴∠A+∠C=∠ADC.
又∵∠A+∠C+∠ADC=360°-70°=290°,
∴∠ADC=145°.
16.解:由题意,得四边形DEFC∽四边形EABF,
则=,
即EF2=DC·AB=4×9=36,∴EF=6.
17.解:(1)由已知得MN=AB=2,DM=AD=BC.
∵将矩形ABCD沿MN对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,
∴=,
∴DM·BC=AB·MN,即BC2=4,
∴BC=2,即矩形ABCD的较长边长为2.
(2)∵余下的矩形EFDC与原矩形ABCD相似,
∴=.
∵AB=CD=2,BC=4,∴DF==1,
∴余下的矩形EFDC的面积=CD·DF=2×1=2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
