北师大版数学九年级上册同步课时练习:4.6 利用相似三角形测高 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:4.6 利用相似三角形测高 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览

文档简介
6 利用相似三角形测高
知识点 1 利用阳光下的影子测高
1.如图在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为 ( )
A.1.5米 B.2.3米 C.3.2米 D.7.8米
2.小刚身高1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,测得影子长为1.1 m,那么小刚举起的手臂超出头顶 ( )
A.0.5 m B.0.55 m C.0.6 m D.2.2 m
3.如图阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,EC=1.2 m,那么窗户的高AB为 m.
知识点 2 利用标杆测高
4.[2020·天水] 如图示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高是 ( )
A.17.5 m B.17 m C.16.5 m D.18 m
5.如图示意图),小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直线上,测得边DE离地面的高度DC为1.4 m,点D到AB的距离DG为6 m.已知DE=30 cm,EF=20 cm,那么树AB的高度为 m.
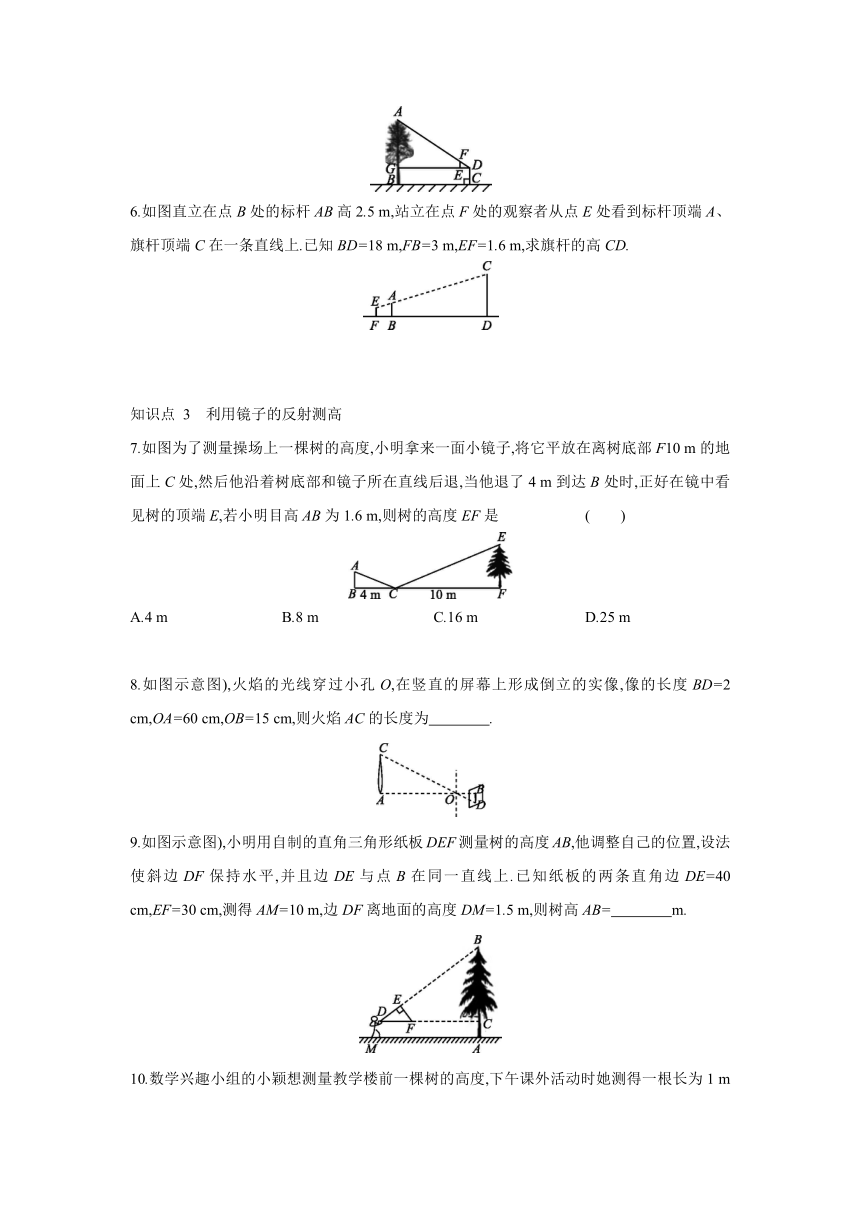
6.如图直立在点B处的标杆AB高2.5 m,站立在点F处的观察者从点E处看到标杆顶端A、旗杆顶端C在一条直线上.已知BD=18 m,FB=3 m,EF=1.6 m,求旗杆的高CD.
知识点 3 利用镜子的反射测高
7.如图为了测量操场上一棵树的高度,小明拿来一面小镜子,将它平放在离树底部F10 m的地面上C处,然后他沿着树底部和镜子所在直线后退,当他退了4 m到达B处时,正好在镜中看见树的顶端E,若小明目高AB为1.6 m,则树的高度EF是 ( )
A.4 m B.8 m C.16 m D.25 m
8.如图示意图),火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则火焰AC的长度为 .
9.如图示意图),小明用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=30 cm,测得AM=10 m,边DF离地面的高度DM=1.5 m,则树高AB= m.
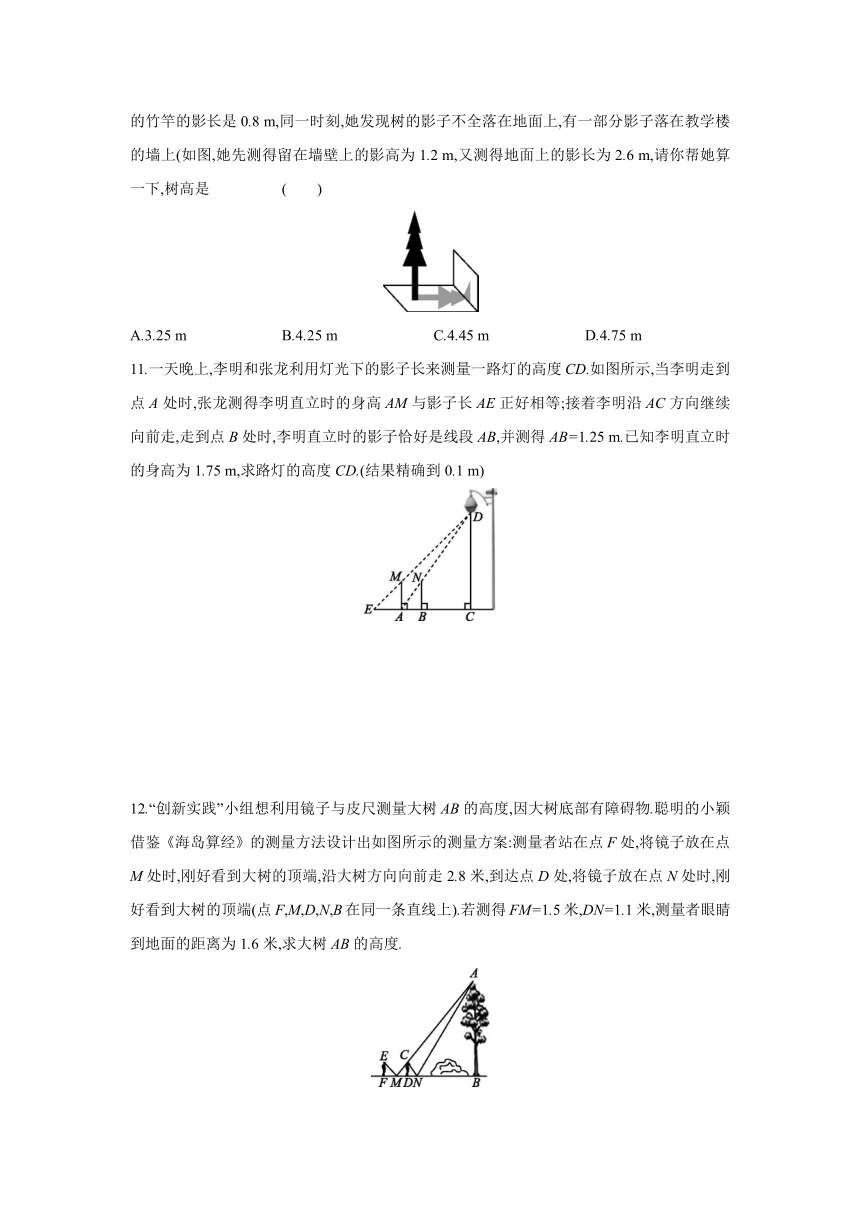
10.数学兴趣小组的小颖想测量教学楼前一棵树的高度,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,同一时刻,她发现树的影子不全落在地面上,有一部分影子落在教学楼的墙上(如图,她先测得留在墙壁上的影高为1.2 m,又测得地面上的影长为2.6 m,请你帮她算一下,树高是 ( )
A.3.25 m B.4.25 m C.4.45 m D.4.75 m
11.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯的高度CD.如图所示,当李明走到点A处时,张龙测得李明直立时的身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时的身高为1.75 m,求路灯的高度CD.(结果精确到0.1 m)
12.“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
答案
1.C
2.A 设小刚举起的手臂超出头顶x m.
根据同一时刻物高与影长成比例,
得=,解得x=0.5.
故选A.
3.1.5 ∵BE∥AD,∴△CBE∽△CAD,∴EC∶CD=BC∶AC,∴1.2∶3=1∶AC,∴AC=2.5 m,∴AB=AC-BC=1.5(m).故答案为1.5.
4.A ∵EB⊥AC,DC⊥AC,∴EB∥DC,
则易得△ABE∽△ACD,
∴=.
∵BE=1.5 m,AB=1.2 m,BC=12.8 m,
∴AC=AB+BC=14(m),
∴=,解得CD=17.5.
即建筑物CD的高是17.5 m.故选A.
5.5.4
6.解:过点E作EH⊥CD于点H,交AB于点G,则EF=GB=DH=1.6 m,EG=FB=3 m,GH=BD=18 m,
∴AG=AB-GB=0.9 m.
由题意,知∠EGA=∠EHC=90°.
又∵∠AEG=∠CEH,
∴△AEG∽△CEH,
∴AG∶CH=EG∶EH,
即=,解得CH=6.3(m),
∴CD=CH+DH=7.9(m).
答:旗杆的高CD为7.9 m.
7.A ∵树和人都垂直于地面,
∴∠EFC=∠ABC=90°.由题意易得∠ECF=∠ACB,∴△EFC∽△ABC,∴=.又AB=1.6 m,BC=4 m,FC=10 m,∴EF=4 m.故选A.
8.8 cm ∵CA∥BD,
∴∠CAO=∠DBO,∠ACO=∠BDO,
∴△AOC∽△BOD,
∴AC∶BD=OA∶OB.
∵BD=2 cm,OA=60 cm,OB=15 cm,
∴AC∶2=60∶15,
解得AC=8(cm).
故火焰AC的长度为8 cm.
9.9 ∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB,∴=.
∵DE=40 cm=0.4 m,EF=30 cm=0.3 m,AC=DM=1.5 m,CD=AM=10 m,
∴=,
∴BC=7.5(m),
∴AB=AC+BC=1.5+7.5=9(m),
即树高为9 m.
10.C 如图图,
根据竹竿的高与其影长的比值和树高与其影长的比值相等,得=,所以BD=0.96(m),所以树在地面上的实际影长是0.96+2.6=3.56(m),再利用竹竿的高与其影长的比值和树高与其影长的比值相等,得=,所以树高=4.45(m).故选C.
11.解:设路灯的高度CD为x m.
∵AM⊥EC,AM=AE,∴∠E=45°.
∵CD⊥EC,∴EC=CD=x m.
∵CD⊥EC,BN⊥EC,
∴∠ABN=∠ACD=90°.
又∵∠BAN=∠CAD,
∴△ABN∽△ACD,
∴=,
即=,
解得x=6.125≈6.1.
经检验,x=6.125是原分式方程的解.
∴路灯的高度CD约为6.1 m.
12.解:设NB的长为x米,
则MB=x+1.1+2.8-1.5=(x+2.4)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,
∴△CND∽△ANB,∴=.
同理,△EMF∽△AMB,∴=.
∵EF=CD,∴=,
∴=,解得x=6.6.
经检验x=6.6是原分式方程的解.
∵△CND∽△ANB,∴=,
∴=,解得AB=9.6.
答:大树AB的高度为9.6米.
知识点 1 利用阳光下的影子测高
1.如图在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为 ( )
A.1.5米 B.2.3米 C.3.2米 D.7.8米
2.小刚身高1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,测得影子长为1.1 m,那么小刚举起的手臂超出头顶 ( )
A.0.5 m B.0.55 m C.0.6 m D.2.2 m
3.如图阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,EC=1.2 m,那么窗户的高AB为 m.
知识点 2 利用标杆测高
4.[2020·天水] 如图示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高是 ( )
A.17.5 m B.17 m C.16.5 m D.18 m
5.如图示意图),小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直线上,测得边DE离地面的高度DC为1.4 m,点D到AB的距离DG为6 m.已知DE=30 cm,EF=20 cm,那么树AB的高度为 m.
6.如图直立在点B处的标杆AB高2.5 m,站立在点F处的观察者从点E处看到标杆顶端A、旗杆顶端C在一条直线上.已知BD=18 m,FB=3 m,EF=1.6 m,求旗杆的高CD.
知识点 3 利用镜子的反射测高
7.如图为了测量操场上一棵树的高度,小明拿来一面小镜子,将它平放在离树底部F10 m的地面上C处,然后他沿着树底部和镜子所在直线后退,当他退了4 m到达B处时,正好在镜中看见树的顶端E,若小明目高AB为1.6 m,则树的高度EF是 ( )
A.4 m B.8 m C.16 m D.25 m
8.如图示意图),火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则火焰AC的长度为 .
9.如图示意图),小明用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=30 cm,测得AM=10 m,边DF离地面的高度DM=1.5 m,则树高AB= m.
10.数学兴趣小组的小颖想测量教学楼前一棵树的高度,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,同一时刻,她发现树的影子不全落在地面上,有一部分影子落在教学楼的墙上(如图,她先测得留在墙壁上的影高为1.2 m,又测得地面上的影长为2.6 m,请你帮她算一下,树高是 ( )
A.3.25 m B.4.25 m C.4.45 m D.4.75 m
11.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯的高度CD.如图所示,当李明走到点A处时,张龙测得李明直立时的身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时的身高为1.75 m,求路灯的高度CD.(结果精确到0.1 m)
12.“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
答案
1.C
2.A 设小刚举起的手臂超出头顶x m.
根据同一时刻物高与影长成比例,
得=,解得x=0.5.
故选A.
3.1.5 ∵BE∥AD,∴△CBE∽△CAD,∴EC∶CD=BC∶AC,∴1.2∶3=1∶AC,∴AC=2.5 m,∴AB=AC-BC=1.5(m).故答案为1.5.
4.A ∵EB⊥AC,DC⊥AC,∴EB∥DC,
则易得△ABE∽△ACD,
∴=.
∵BE=1.5 m,AB=1.2 m,BC=12.8 m,
∴AC=AB+BC=14(m),
∴=,解得CD=17.5.
即建筑物CD的高是17.5 m.故选A.
5.5.4
6.解:过点E作EH⊥CD于点H,交AB于点G,则EF=GB=DH=1.6 m,EG=FB=3 m,GH=BD=18 m,
∴AG=AB-GB=0.9 m.
由题意,知∠EGA=∠EHC=90°.
又∵∠AEG=∠CEH,
∴△AEG∽△CEH,
∴AG∶CH=EG∶EH,
即=,解得CH=6.3(m),
∴CD=CH+DH=7.9(m).
答:旗杆的高CD为7.9 m.
7.A ∵树和人都垂直于地面,
∴∠EFC=∠ABC=90°.由题意易得∠ECF=∠ACB,∴△EFC∽△ABC,∴=.又AB=1.6 m,BC=4 m,FC=10 m,∴EF=4 m.故选A.
8.8 cm ∵CA∥BD,
∴∠CAO=∠DBO,∠ACO=∠BDO,
∴△AOC∽△BOD,
∴AC∶BD=OA∶OB.
∵BD=2 cm,OA=60 cm,OB=15 cm,
∴AC∶2=60∶15,
解得AC=8(cm).
故火焰AC的长度为8 cm.
9.9 ∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB,∴=.
∵DE=40 cm=0.4 m,EF=30 cm=0.3 m,AC=DM=1.5 m,CD=AM=10 m,
∴=,
∴BC=7.5(m),
∴AB=AC+BC=1.5+7.5=9(m),
即树高为9 m.
10.C 如图图,
根据竹竿的高与其影长的比值和树高与其影长的比值相等,得=,所以BD=0.96(m),所以树在地面上的实际影长是0.96+2.6=3.56(m),再利用竹竿的高与其影长的比值和树高与其影长的比值相等,得=,所以树高=4.45(m).故选C.
11.解:设路灯的高度CD为x m.
∵AM⊥EC,AM=AE,∴∠E=45°.
∵CD⊥EC,∴EC=CD=x m.
∵CD⊥EC,BN⊥EC,
∴∠ABN=∠ACD=90°.
又∵∠BAN=∠CAD,
∴△ABN∽△ACD,
∴=,
即=,
解得x=6.125≈6.1.
经检验,x=6.125是原分式方程的解.
∴路灯的高度CD约为6.1 m.
12.解:设NB的长为x米,
则MB=x+1.1+2.8-1.5=(x+2.4)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,
∴△CND∽△ANB,∴=.
同理,△EMF∽△AMB,∴=.
∵EF=CD,∴=,
∴=,解得x=6.6.
经检验x=6.6是原分式方程的解.
∵△CND∽△ANB,∴=,
∴=,解得AB=9.6.
答:大树AB的高度为9.6米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
