北师大版数学九年级上册同步课时练习:6.2 第1课时 反比例函数的图象 (word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步课时练习:6.2 第1课时 反比例函数的图象 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 457.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 07:05:23 | ||
图片预览


文档简介
2 第1课时 反比例函数的图象
知识点1 反比例函数的图象
1.已知反比例函数y=,则其图象在平面直角坐标系中可能是 ( )
2.下列说法错误的是 ( )
A.反比例函数的图象是双曲线
B.画反比例函数的图象时,描点后注意用平滑的曲线连接
C.反比例函数的图象与坐标轴没有交点
D.反比例函数的图象经过原点
3.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是 ( )
A.y= B.y=- C.y= D.y=-
4.已知反比例函数y=-,当x>0时,它的图象在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.反比例函数y=的图象分布在第二、四象限,则点(m,m-2)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是 ( )
A.(4,-1) B.(-,1) C.(-4,-1) D.(,2)
7.反比例函数y=(k≠0)的图象的两个分支分别位于第 象限.
8.反比例函数y=的图象的一支,根据图象可知常数m的取值范围是 .
9.在作出反比例函数y=的图象,并根据图象解答下列问题:
(1)当x=4时,求y的值;
(2)当y=-2时,求x的值.
知识点 2 反比例函数图象的对称性
10.关于反比例函数y=图象的对称性,下列叙述错误的是 ( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
11.如图在平面直角坐标系中,正方形的中心在原点O处,且正方形的一组对边与x轴平行.若正方形的边长是2,则图中阴影部分的面积等于 .
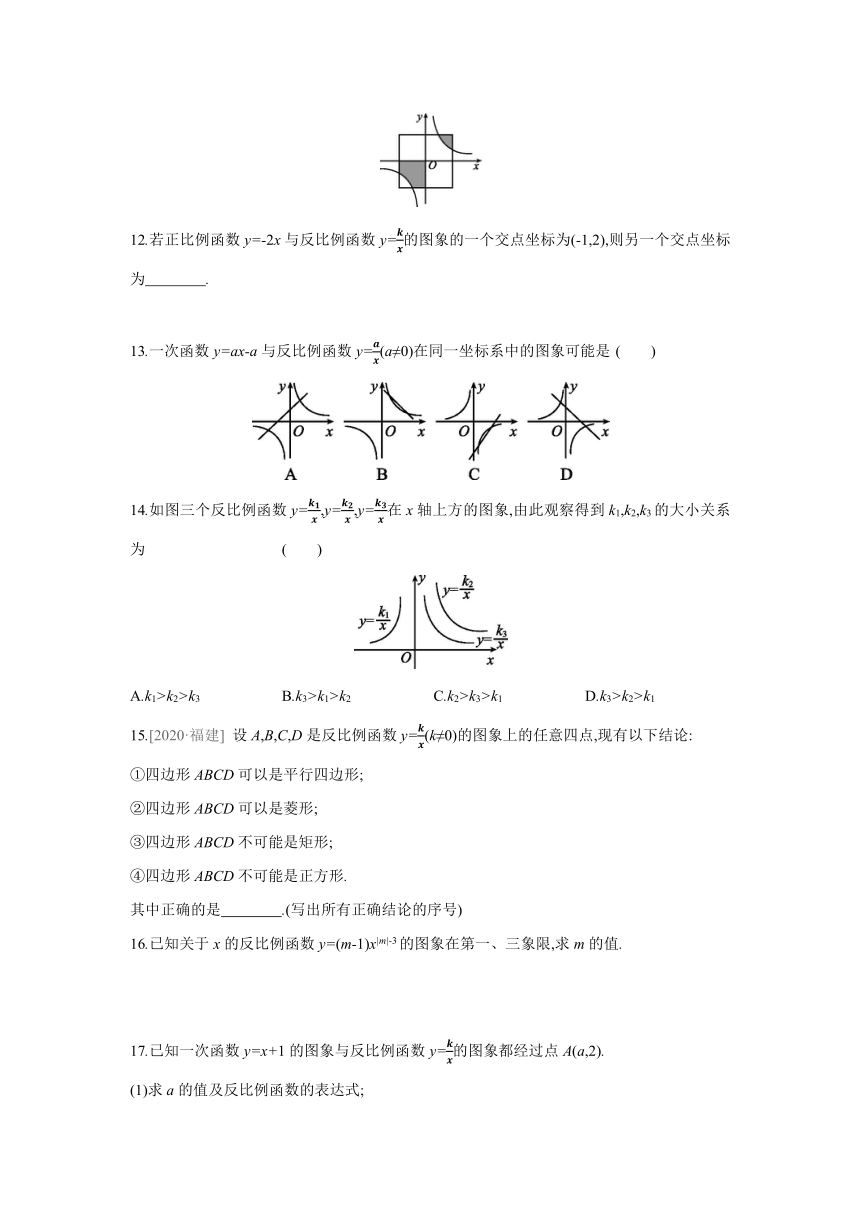
12.若正比例函数y=-2x与反比例函数y=的图象的一个交点坐标为(-1,2),则另一个交点坐标为 .
13.一次函数y=ax-a与反比例函数y=(a≠0)在同一坐标系中的图象可能是 ( )
14.如图三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 ( )
A.k1>k2>k3 B.k3>k1>k2 C.k2>k3>k1 D.k3>k2>k1
15.[2020·福建] 设A,B,C,D是反比例函数y=(k≠0)的图象上的任意四点,现有以下结论:
①四边形ABCD可以是平行四边形;
②四边形ABCD可以是菱形;
③四边形ABCD不可能是矩形;
④四边形ABCD不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
16.已知关于x的反比例函数y=(m-1)x|m|-3的图象在第一、三象限,求m的值.
17.已知一次函数y=x+1的图象与反比例函数y=的图象都经过点A(a,2).
(1)求a的值及反比例函数的表达式;
(2)判断点B(2,)是否在该反比例函数的图象上,并说明理由.
18.已知反比例函数y=(m为常数)的图象在第一、三象限.
(1)求m的取值范围.
(2)如图若该反比例函数的图象经过 ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求出函数的表达式;
②设点P是该反比例函数图象上的一点.
(a)若OD=OP,则点P的坐标为 ;
(b)若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 .
答案
1.C
2.D 3.D
4.D ∵k=-2<0,
∴其图象位于第二、四象限,
∴当x>0时,它的图象位于第四象限.
故选D.
5.C
6.A 将点(-1,4)代入y=,
得k=-4,
∴y=,
∴点(4,-1)在该函数图象上.
故选A.
7.一、三
8.m>5
9.解:列表:
x … -6 -4 -3 -2 2 3 4 6 …
y … -2 -3 -4 -6 6 4 3 2 …
描点、连线,如图图所示.
(1)当x=4时,y=3.
(2)当y=-2时,x=-6.
10.D
11.1 12.(1,-2) 13.D
14.C
15.①④
16.解:∵反比例函数y=(m-1)x|m|-3的图象在第一、三象限,
∴
解得m=2,
即m的值是2.
17.解:(1)∵一次函数y=x+1的图象经过点A(a,2),
∴2=a+1,解得a=1.
又∵反比例函数y=的图象经过点A(1,2),
∴2=,解得k=2,∴y=.
即a的值为1,反比例函数的表达式为y=.
(2)点B在该反比例函数的图象上.
理由:∵2×=2=k,
∴点B在该反比例函数的图象上.
18.解:(1)由题意知1-2m>0,解得m<.
(2)①∵四边形ABOD是平行四边形,
∴AD∥BO且AD=BO.
∵A(0,3),B(-2,0),O(0,0),
∴点D的坐标是(2,3),
∴=3,即1-2m=6,
∴函数的表达式为y=.
②(a)(3,2)或(-2,-3)或(-3,-2) (b)4
知识点1 反比例函数的图象
1.已知反比例函数y=,则其图象在平面直角坐标系中可能是 ( )
2.下列说法错误的是 ( )
A.反比例函数的图象是双曲线
B.画反比例函数的图象时,描点后注意用平滑的曲线连接
C.反比例函数的图象与坐标轴没有交点
D.反比例函数的图象经过原点
3.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是 ( )
A.y= B.y=- C.y= D.y=-
4.已知反比例函数y=-,当x>0时,它的图象在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.反比例函数y=的图象分布在第二、四象限,则点(m,m-2)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是 ( )
A.(4,-1) B.(-,1) C.(-4,-1) D.(,2)
7.反比例函数y=(k≠0)的图象的两个分支分别位于第 象限.
8.反比例函数y=的图象的一支,根据图象可知常数m的取值范围是 .
9.在作出反比例函数y=的图象,并根据图象解答下列问题:
(1)当x=4时,求y的值;
(2)当y=-2时,求x的值.
知识点 2 反比例函数图象的对称性
10.关于反比例函数y=图象的对称性,下列叙述错误的是 ( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
11.如图在平面直角坐标系中,正方形的中心在原点O处,且正方形的一组对边与x轴平行.若正方形的边长是2,则图中阴影部分的面积等于 .
12.若正比例函数y=-2x与反比例函数y=的图象的一个交点坐标为(-1,2),则另一个交点坐标为 .
13.一次函数y=ax-a与反比例函数y=(a≠0)在同一坐标系中的图象可能是 ( )
14.如图三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 ( )
A.k1>k2>k3 B.k3>k1>k2 C.k2>k3>k1 D.k3>k2>k1
15.[2020·福建] 设A,B,C,D是反比例函数y=(k≠0)的图象上的任意四点,现有以下结论:
①四边形ABCD可以是平行四边形;
②四边形ABCD可以是菱形;
③四边形ABCD不可能是矩形;
④四边形ABCD不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
16.已知关于x的反比例函数y=(m-1)x|m|-3的图象在第一、三象限,求m的值.
17.已知一次函数y=x+1的图象与反比例函数y=的图象都经过点A(a,2).
(1)求a的值及反比例函数的表达式;
(2)判断点B(2,)是否在该反比例函数的图象上,并说明理由.
18.已知反比例函数y=(m为常数)的图象在第一、三象限.
(1)求m的取值范围.
(2)如图若该反比例函数的图象经过 ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求出函数的表达式;
②设点P是该反比例函数图象上的一点.
(a)若OD=OP,则点P的坐标为 ;
(b)若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 .
答案
1.C
2.D 3.D
4.D ∵k=-2<0,
∴其图象位于第二、四象限,
∴当x>0时,它的图象位于第四象限.
故选D.
5.C
6.A 将点(-1,4)代入y=,
得k=-4,
∴y=,
∴点(4,-1)在该函数图象上.
故选A.
7.一、三
8.m>5
9.解:列表:
x … -6 -4 -3 -2 2 3 4 6 …
y … -2 -3 -4 -6 6 4 3 2 …
描点、连线,如图图所示.
(1)当x=4时,y=3.
(2)当y=-2时,x=-6.
10.D
11.1 12.(1,-2) 13.D
14.C
15.①④
16.解:∵反比例函数y=(m-1)x|m|-3的图象在第一、三象限,
∴
解得m=2,
即m的值是2.
17.解:(1)∵一次函数y=x+1的图象经过点A(a,2),
∴2=a+1,解得a=1.
又∵反比例函数y=的图象经过点A(1,2),
∴2=,解得k=2,∴y=.
即a的值为1,反比例函数的表达式为y=.
(2)点B在该反比例函数的图象上.
理由:∵2×=2=k,
∴点B在该反比例函数的图象上.
18.解:(1)由题意知1-2m>0,解得m<.
(2)①∵四边形ABOD是平行四边形,
∴AD∥BO且AD=BO.
∵A(0,3),B(-2,0),O(0,0),
∴点D的坐标是(2,3),
∴=3,即1-2m=6,
∴函数的表达式为y=.
②(a)(3,2)或(-2,-3)或(-3,-2) (b)4
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
