人教版 九年级上册 22.1.2 二次函数y=ax2+k的图像和性质导 学案(无答案)
文档属性
| 名称 | 人教版 九年级上册 22.1.2 二次函数y=ax2+k的图像和性质导 学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 80.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 09:59:32 | ||
图片预览

文档简介
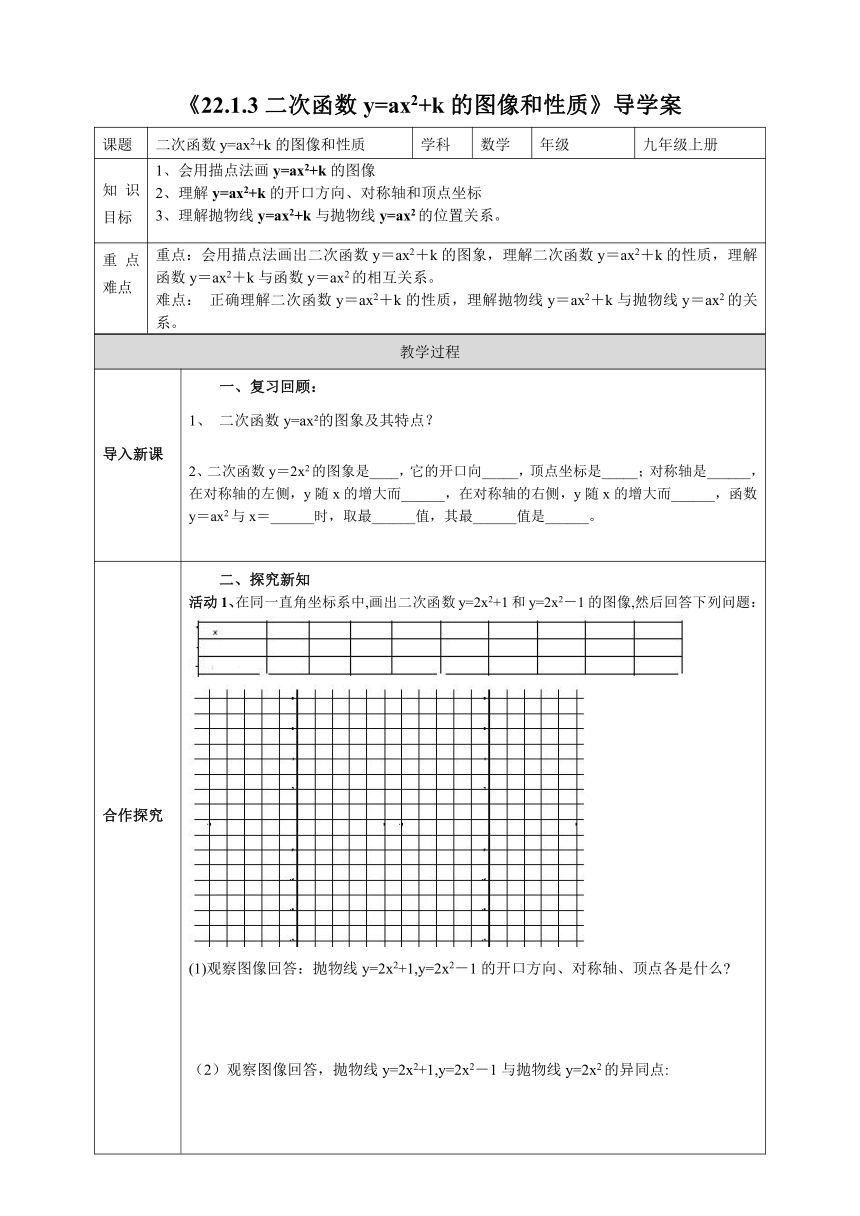
《22.1.3二次函数y=ax2+k的图像和性质》导学案
课题 二次函数y=ax2+k的图像和性质 学科 数学 年级 九年级上册
知识目标 1、会用描点法画y=ax2+k的图像2、理解y=ax2+k的开口方向、对称轴和顶点坐标3、理解抛物线y=ax2+k与抛物线y=ax2的位置关系。
重点难点 重点:会用描点法画出二次函数y=ax2+k的图象,理解二次函数y=ax2+k的性质,理解函数y=ax2+k与函数y=ax2的相互关系。 难点: 正确理解二次函数y=ax2+k的性质,理解抛物线y=ax2+k与抛物线y=ax2的关系。
教学过程
导入新课 一、复习回顾: 1、 二次函数y=ax 的图象及其特点?2、二次函数y=2x2的图象 ( http: / / www.21cnjy.com )是____,它的开口向_____,顶点坐标是_____;对称轴是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,函数y=ax2与x=______时,取最______值,其最______值是______。
合作探究 二、探究新知活动1、在同一直角坐标系中,画出二次函数y=2x2+1和y=2x2-1的图像,然后回答下列问题:(1)观察图像回答:抛物线y=2x2+1,y=2x2-1的开口方向、对称轴、顶点各是什么 (2)观察图像回答,抛物线y=2x2+1,y=2x2-1与抛物线y=2x2的异同点:活动2、用类比的方法讨论y=-x2+3、y=-x2和y=-x2-2顶点、对称轴、位置关系。通过上述活动,总结抛物线y=ax2+k与抛物线y=ax2在位置上有什么关系?它们的性质有什么区别和联系?●归纳:平移的规律:1、若k>0,将抛物线y=ax2向上平移k个单位,那么它的解析式为____________,向下平移k个单位,那么它的解析式为_____________.(记为:上加下减)2、性质:①当a>0时,抛物线y=ax2+k的开口_______ ,对称轴是_______ ,顶点坐标是_______,在对称轴的左侧,y随x的增大而_______,在对称轴的右侧,y随x的增大而_______,当x=_______时,取得最_______值,这个值等于_______; ②当a<0时,抛物线y=ax2+k的开口_______ ,对称轴是_______ ,顶点坐标是 _______ ,在对称轴的左侧,y随x的增大而_______ ,在对称轴的右侧,y随x的增大而_______,当x= _______时,取得最_______ 值,这个值等于_______。例、已知抛物线y=x2,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
自主尝试 活动1基础练习:在同一直角坐标系中,画出下列二次函数的图象:y=-3x2+4 y=-3x2 y=-3x2-7将函数y=-3x2+4的图象向______平移______个单位可得y=-3x2的图象;将y=-3x2-7的图象向______平移______个单位得到y=-3x2的图象。将y=x2-7的图象向______平移______个单位可得到 y=x2+2的图象。3、将抛物线y=4x2向上平移3个单位,所得的抛物线的函数式是__________________。4、抛物线y= 2x2+3的顶点坐标是________,对称轴是________,在___侧,y随着x的增大而增大;在___侧,y随着x的增大而减小,当x= _____时,函数y的值最大,最大值是________ ,它是由抛物线y= 2x2线怎样平移得到的__________.活动2强化练习:1、将抛物线 y=-x2向下平移多少个单位可以经过(3,-14),并求出这时抛物线的解析式.2、写出一个顶点坐标是(0,-3),开口方向与抛物线 y= -x2的方向相反,形状相同的抛物线解析式:__________.3、已知抛物线y=2x2-1上有两点(a, m)(b, n),且a n B、m = n C、m < n D、不能确定变式1:若a>b>0,其他条件不变,则m与n的大小关系为( )变式2:若a课堂小结
布置作业 1.请同学们做一做P33课后练习;2.练习册这一个课时内容。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
课题 二次函数y=ax2+k的图像和性质 学科 数学 年级 九年级上册
知识目标 1、会用描点法画y=ax2+k的图像2、理解y=ax2+k的开口方向、对称轴和顶点坐标3、理解抛物线y=ax2+k与抛物线y=ax2的位置关系。
重点难点 重点:会用描点法画出二次函数y=ax2+k的图象,理解二次函数y=ax2+k的性质,理解函数y=ax2+k与函数y=ax2的相互关系。 难点: 正确理解二次函数y=ax2+k的性质,理解抛物线y=ax2+k与抛物线y=ax2的关系。
教学过程
导入新课 一、复习回顾: 1、 二次函数y=ax 的图象及其特点?2、二次函数y=2x2的图象 ( http: / / www.21cnjy.com )是____,它的开口向_____,顶点坐标是_____;对称轴是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,函数y=ax2与x=______时,取最______值,其最______值是______。
合作探究 二、探究新知活动1、在同一直角坐标系中,画出二次函数y=2x2+1和y=2x2-1的图像,然后回答下列问题:(1)观察图像回答:抛物线y=2x2+1,y=2x2-1的开口方向、对称轴、顶点各是什么 (2)观察图像回答,抛物线y=2x2+1,y=2x2-1与抛物线y=2x2的异同点:活动2、用类比的方法讨论y=-x2+3、y=-x2和y=-x2-2顶点、对称轴、位置关系。通过上述活动,总结抛物线y=ax2+k与抛物线y=ax2在位置上有什么关系?它们的性质有什么区别和联系?●归纳:平移的规律:1、若k>0,将抛物线y=ax2向上平移k个单位,那么它的解析式为____________,向下平移k个单位,那么它的解析式为_____________.(记为:上加下减)2、性质:①当a>0时,抛物线y=ax2+k的开口_______ ,对称轴是_______ ,顶点坐标是_______,在对称轴的左侧,y随x的增大而_______,在对称轴的右侧,y随x的增大而_______,当x=_______时,取得最_______值,这个值等于_______; ②当a<0时,抛物线y=ax2+k的开口_______ ,对称轴是_______ ,顶点坐标是 _______ ,在对称轴的左侧,y随x的增大而_______ ,在对称轴的右侧,y随x的增大而_______,当x= _______时,取得最_______ 值,这个值等于_______。例、已知抛物线y=x2,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
自主尝试 活动1基础练习:在同一直角坐标系中,画出下列二次函数的图象:y=-3x2+4 y=-3x2 y=-3x2-7将函数y=-3x2+4的图象向______平移______个单位可得y=-3x2的图象;将y=-3x2-7的图象向______平移______个单位得到y=-3x2的图象。将y=x2-7的图象向______平移______个单位可得到 y=x2+2的图象。3、将抛物线y=4x2向上平移3个单位,所得的抛物线的函数式是__________________。4、抛物线y= 2x2+3的顶点坐标是________,对称轴是________,在___侧,y随着x的增大而增大;在___侧,y随着x的增大而减小,当x= _____时,函数y的值最大,最大值是________ ,它是由抛物线y= 2x2线怎样平移得到的__________.活动2强化练习:1、将抛物线 y=-x2向下平移多少个单位可以经过(3,-14),并求出这时抛物线的解析式.2、写出一个顶点坐标是(0,-3),开口方向与抛物线 y= -x2的方向相反,形状相同的抛物线解析式:__________.3、已知抛物线y=2x2-1上有两点(a, m)(b, n),且a
布置作业 1.请同学们做一做P33课后练习;2.练习册这一个课时内容。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
