第六章立体几何初步之空间“三角”问题 课件(共46张PPT)
文档属性
| 名称 | 第六章立体几何初步之空间“三角”问题 课件(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 15:59:24 | ||
图片预览











文档简介
(共46张PPT)
第六章立体几何初步
专题课:空间【三角】问题
北师大(2019)必修2
目
录
1.异面直线成角
2.直线与平面成角
3.二面角的平面角
空间【三角】问题
环节一
异面直线所成角
异面直线所成角
直线,b是异面直线,经过空间任意一点o,作直线‘,b’,使 把a‘和b'所成的锐角或直角记作异面直线和b所成的角
异面直线所成角的范围是
求法
一、几何法(先作图后求)
①平移法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线或利用中位线;
②补形法: 把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线间的关系.
一般来说,平移法是最常用的,应作为求异面直线所成的角的首选方法.同时要特别注意异面直线所成的角的范围:
求法
二、向量法(高一暂不讲)
用向量求解两条异面直线的夹角问题,首先应根据图形取定基底或建立空间直角坐标系,然后分别求出与这两条异面直线共线的向量m和n、再由 的值来确定异面直线夹角的大小.
【例1】在正四面体 中,E、F分别是AD、BC的中点,连CE、AF,求异面直线CE与AF所成角余弦值.
【解析】 如图,连DF,设O为DF的中点,连EO、OC,则 故在三角形OEC中, (或其补角)即为异面直线AF与CE所成角,设 则
由余弦定理得:
故所求异面直线CE与AF所成角的余弦大小为
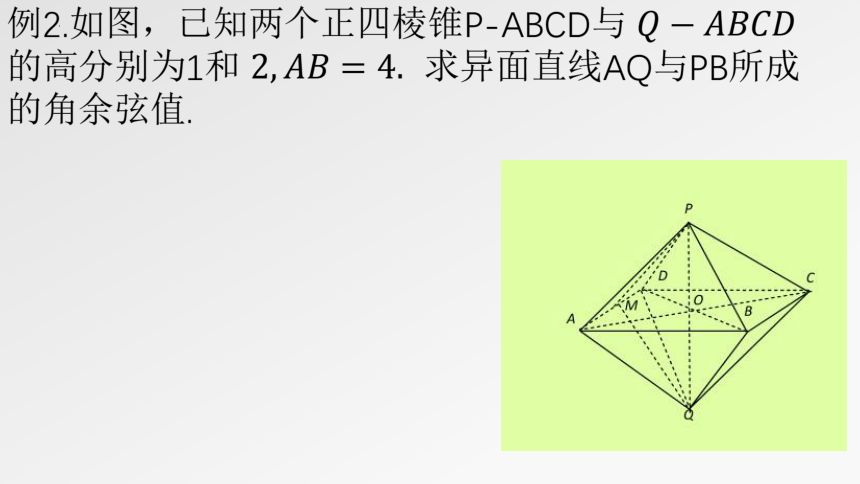
例2.如图,已知两个正四棱锥P-ABCD与 的高分别为1和 求异面直线AQ与PB所成的角余弦值.
连结AC、BD设 由PQ上平面ABCD及正四棱锥的性质可知O在PQ上,从而P、A、Q、C四点共面、取OC的中点N,连接PN.
因为 所以
从而 (或其补角)是异面直线AQ与PB所成的角.
因为
所以
从而异面直线AQ与PB所成的角是
解后思
【平移法】即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角.就是把异面直线所成的角通过平移转化为两条相交直线所成的角,化为平面问题,具体地讲是选择“特殊点”作异面直线的平行线,构作含异面直线所成角(或其补角)的三角形,再求之。
【例3】如图,在长方体 中,已知 求异面直线 与AC所成角的余弦值的大小.
【解析】 在长方体 的一旁补上一个全等的长方体 连接BF、D1F,则BF//AC.于是BF与BD;所成的角(或其补角)即为AC与 所成的角.
设
在三角形 中,由余弦定理得:
补形法
把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体等,其目的在于易于发现两条异面直线的关系.
1.求异面直线的步骤:
一作,二证,三指,四计算,五答
2.关键:在空间内找到一个恰当的点O,通过平移直线,作出异面直线所成的角把空间异面直线所成的角,转化为平面内相交直线所成的锐角或直角
3.解Rt▲或斜三角形,用余弦定理求角时,
注意异面直线所成的角范围是
小结
环节二
线面角
定义
(1)平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和平面所成的角.
(2)直线和平面垂直——直线与平面所成的角是直角.
(3)直线和平面平行或直线在平面内——直线与平面所成的角是 度的角.
理解
2.按照定义,在求直线和平面所成的角时,应按下述三种情况依次进行考虑:
(1) 直线和平面平行或直线在平面内时,直线和平面所成的角是 角;
(2)直线和平面垂直时,直线和平面所成的角是直角;
(3)直线和平面斜交时,直线和平面所在的角是指直线和它在平面内的射影所成的锐角.
3.斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角.
求法
一、几何法(定义法)
求直线与平面所成的角,一般先确定直线与平面的交点(斜足),然后在直线上取一点(除斜足外),作平面的垂线,再连接垂足和斜足(即得直接在平面内的射影),最后解由垂线、斜线、射影所组成的直角三角形,求出直线与平面所成的角.
解题步骤:作、证、算
求法
二、法向量法
与平面的斜线共线的向量 和这个平面的一个法向量 的夹角 (或者说其补角)是这条斜线与该平面夹角的余角.
即:若直线AB与平面a所成的角为θ,平面a的法向量为 与 的夹角为@
故
求法
二、等积法
在几何法中,如果垂线段垂足无法确定或者垂线段长度不易求出,可以转化为三棱锥等积法
例1.如图,在四棱锥 中,底面ABCD是正方形,侧棱 底面ABCD,PD=DC,E是PC的中点.求EB与底面ABCD所成的角的正切值.
解:作 交DC于F.连结BF.设正方形ABCD的边长为a.
QPDL底面ABCD, F为CD的中点.
EF⊥底面ABCD,BF为BE在底面ABCD内的射影,故 为直线EB与底面ABCD所成的角.
在 中,
在 中,
例2 (2004年重庆高考题)如图,四棱锥 面是正方形, 底面 。
若 求直线AC与平面EAM所成角的正弦值.
解:连结BD交AC于0、连结BE,过0作BE的垂线OH,垂足 H在BE上,易知PD1面MAE,故 又 战OH//DE,因此OH1面MAE.
连结AH,则△HAO是所足要求的线AC与面NAE所成的角
设AB=a,则
因Rt△ADE ~ Rt△PDA,故
从而在
中
例2.四棱锥 底面ABCD,AB//CD,AB⊥AD,AB=AD ,E、F分别是PC、PD的中点。求直线AC与平面ABEF所成角的正弦值。
如图,将平面ABEF向右进行延展,作 面ABEF,连接AH、AE,则 为直线AC与平面ABEF所成角
因为 所P以 /面ABCD。
因为F为PD 中图点, 底面ABCD,所以点E、F到面ABCD的距离相等。
所以点F到面ABCD的距离为 所以点E到面ABCD的距离
因为
所以
又 所以
故直线AC与面ABEF所成角的正弦值为
环节三
面面角
1、二面角的定义
从空间一直线出发的两个半平面所组成的图形叫做二面角
记作:
2、二面角的平面角
一个平面垂直于二面角 的棱,并与两半平面分别相交于射线PA、PB垂足为P,则 叫做二面角 的平面角
求法
1.定义法
依据二面角的平面角的定义,只要找到二面角的棱的垂面便可获得二面角的平面角.
例1 如图,二面角 -β内一点P, 于A,PB 于B,△APB=60°,求二面角 的大小.
解:设PA与PB所确定的平面为Y,设 连结AO,BO,设Y∩a=AO,Y∩β=BO.
: l;同理:
为二面角 的平面角.
四边形AOBP为平面四边形, 即二面角α- 的大小为
本题如果是作 于O,再连接BO,则不易证明 即所求角.
依据二面角平面角的定义可得:以二面角棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角是二面角的平面角.据此,只要找到这样的两条射线即可.
评注
求法
2.三垂线法
要作平面角,首先找“垂线"(指其中一个半平面的垂线);找不到“垂线”找“垂面”(指其中一个半平面的垂面);找不到“垂面”作“垂线”,构造三垂线定理或逆定理条件得到二面角的平面角.
例2 如图,在底面是直角梯形的四棱锥 ABCD中, 面ABCD, 求面SCD与面SBA所成二面角的正切值.
解:题设中已有“线面垂直”条件,只需找到棱,依据三垂线定理或逆定理条件得到二面角的平面角.
延长BA、CD相交于点E,连接SE,则SE是所求二面角的棱.
AD/BC,BC=2AD, EA=AB=SA,.. 得面SEB上面EBC,EB是交线,又BC上EB,BC上面SEB,SB是SC在面SEB上的射影,SC1SE,△BSC是所求二面角的平面角.
SB, 即所求二面角的正切值为
求法
3、辅助平面法
(1)求二面角 的大小,可转化为求β的拓展半平面与a所成二面角大小,取其邻补角即可,
(2)对于一些无棱二面角问题有时我们不必去找棱,而通过移面法去求另一个平面角相等的二面角.即把其中一个平面平行移动使之与另一半平面相交、形成一个新的有棱二面角,求出有棱二面角的度数即为无棱二面角度数.
例3.在正方体 中,求二面角 的大小.
略解:本题的常规解法是在半平面, 和 内构作二面角的平面角,但过程较繁、而利用半平面 的延伸面A;B,D解之,过程十分简洁.
作 ,垂足为E,连结A,E,. 是二面角 的平面角.
设正方体棱长为a,可得 即二面角 大小为 又二面角 与 C互为补角,二面角 大小为
求法
4、法向量法
环节四
学以致用
1.在正方体 中,
(1)求异面直线AB与 所成的角;
(2)求异面直线AB和 所成的角
2.等腰 的顶点A在平面α外底边BC在平面α内,已知底边长 腰长 又知点A到平面α的垂线段
(1)等腰 的高AE的长;
(2)斜线AE和平面α所成的角的大小(精确到1°).
15
42°
3.已知P为二面角 内一点,且P到两个半平面的距离都等于P到棱的距离的一半,则这个二面角的度数是多少
第六章立体几何初步
专题课:空间【三角】问题
北师大(2019)必修2
目
录
1.异面直线成角
2.直线与平面成角
3.二面角的平面角
空间【三角】问题
环节一
异面直线所成角
异面直线所成角
直线,b是异面直线,经过空间任意一点o,作直线‘,b’,使 把a‘和b'所成的锐角或直角记作异面直线和b所成的角
异面直线所成角的范围是
求法
一、几何法(先作图后求)
①平移法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线或利用中位线;
②补形法: 把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线间的关系.
一般来说,平移法是最常用的,应作为求异面直线所成的角的首选方法.同时要特别注意异面直线所成的角的范围:
求法
二、向量法(高一暂不讲)
用向量求解两条异面直线的夹角问题,首先应根据图形取定基底或建立空间直角坐标系,然后分别求出与这两条异面直线共线的向量m和n、再由 的值来确定异面直线夹角的大小.
【例1】在正四面体 中,E、F分别是AD、BC的中点,连CE、AF,求异面直线CE与AF所成角余弦值.
【解析】 如图,连DF,设O为DF的中点,连EO、OC,则 故在三角形OEC中, (或其补角)即为异面直线AF与CE所成角,设 则
由余弦定理得:
故所求异面直线CE与AF所成角的余弦大小为
例2.如图,已知两个正四棱锥P-ABCD与 的高分别为1和 求异面直线AQ与PB所成的角余弦值.
连结AC、BD设 由PQ上平面ABCD及正四棱锥的性质可知O在PQ上,从而P、A、Q、C四点共面、取OC的中点N,连接PN.
因为 所以
从而 (或其补角)是异面直线AQ与PB所成的角.
因为
所以
从而异面直线AQ与PB所成的角是
解后思
【平移法】即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角.就是把异面直线所成的角通过平移转化为两条相交直线所成的角,化为平面问题,具体地讲是选择“特殊点”作异面直线的平行线,构作含异面直线所成角(或其补角)的三角形,再求之。
【例3】如图,在长方体 中,已知 求异面直线 与AC所成角的余弦值的大小.
【解析】 在长方体 的一旁补上一个全等的长方体 连接BF、D1F,则BF//AC.于是BF与BD;所成的角(或其补角)即为AC与 所成的角.
设
在三角形 中,由余弦定理得:
补形法
把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体等,其目的在于易于发现两条异面直线的关系.
1.求异面直线的步骤:
一作,二证,三指,四计算,五答
2.关键:在空间内找到一个恰当的点O,通过平移直线,作出异面直线所成的角把空间异面直线所成的角,转化为平面内相交直线所成的锐角或直角
3.解Rt▲或斜三角形,用余弦定理求角时,
注意异面直线所成的角范围是
小结
环节二
线面角
定义
(1)平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和平面所成的角.
(2)直线和平面垂直——直线与平面所成的角是直角.
(3)直线和平面平行或直线在平面内——直线与平面所成的角是 度的角.
理解
2.按照定义,在求直线和平面所成的角时,应按下述三种情况依次进行考虑:
(1) 直线和平面平行或直线在平面内时,直线和平面所成的角是 角;
(2)直线和平面垂直时,直线和平面所成的角是直角;
(3)直线和平面斜交时,直线和平面所在的角是指直线和它在平面内的射影所成的锐角.
3.斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角.
求法
一、几何法(定义法)
求直线与平面所成的角,一般先确定直线与平面的交点(斜足),然后在直线上取一点(除斜足外),作平面的垂线,再连接垂足和斜足(即得直接在平面内的射影),最后解由垂线、斜线、射影所组成的直角三角形,求出直线与平面所成的角.
解题步骤:作、证、算
求法
二、法向量法
与平面的斜线共线的向量 和这个平面的一个法向量 的夹角 (或者说其补角)是这条斜线与该平面夹角的余角.
即:若直线AB与平面a所成的角为θ,平面a的法向量为 与 的夹角为@
故
求法
二、等积法
在几何法中,如果垂线段垂足无法确定或者垂线段长度不易求出,可以转化为三棱锥等积法
例1.如图,在四棱锥 中,底面ABCD是正方形,侧棱 底面ABCD,PD=DC,E是PC的中点.求EB与底面ABCD所成的角的正切值.
解:作 交DC于F.连结BF.设正方形ABCD的边长为a.
QPDL底面ABCD, F为CD的中点.
EF⊥底面ABCD,BF为BE在底面ABCD内的射影,故 为直线EB与底面ABCD所成的角.
在 中,
在 中,
例2 (2004年重庆高考题)如图,四棱锥 面是正方形, 底面 。
若 求直线AC与平面EAM所成角的正弦值.
解:连结BD交AC于0、连结BE,过0作BE的垂线OH,垂足 H在BE上,易知PD1面MAE,故 又 战OH//DE,因此OH1面MAE.
连结AH,则△HAO是所足要求的线AC与面NAE所成的角
设AB=a,则
因Rt△ADE ~ Rt△PDA,故
从而在
中
例2.四棱锥 底面ABCD,AB//CD,AB⊥AD,AB=AD ,E、F分别是PC、PD的中点。求直线AC与平面ABEF所成角的正弦值。
如图,将平面ABEF向右进行延展,作 面ABEF,连接AH、AE,则 为直线AC与平面ABEF所成角
因为 所P以 /面ABCD。
因为F为PD 中图点, 底面ABCD,所以点E、F到面ABCD的距离相等。
所以点F到面ABCD的距离为 所以点E到面ABCD的距离
因为
所以
又 所以
故直线AC与面ABEF所成角的正弦值为
环节三
面面角
1、二面角的定义
从空间一直线出发的两个半平面所组成的图形叫做二面角
记作:
2、二面角的平面角
一个平面垂直于二面角 的棱,并与两半平面分别相交于射线PA、PB垂足为P,则 叫做二面角 的平面角
求法
1.定义法
依据二面角的平面角的定义,只要找到二面角的棱的垂面便可获得二面角的平面角.
例1 如图,二面角 -β内一点P, 于A,PB 于B,△APB=60°,求二面角 的大小.
解:设PA与PB所确定的平面为Y,设 连结AO,BO,设Y∩a=AO,Y∩β=BO.
: l;同理:
为二面角 的平面角.
四边形AOBP为平面四边形, 即二面角α- 的大小为
本题如果是作 于O,再连接BO,则不易证明 即所求角.
依据二面角平面角的定义可得:以二面角棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角是二面角的平面角.据此,只要找到这样的两条射线即可.
评注
求法
2.三垂线法
要作平面角,首先找“垂线"(指其中一个半平面的垂线);找不到“垂线”找“垂面”(指其中一个半平面的垂面);找不到“垂面”作“垂线”,构造三垂线定理或逆定理条件得到二面角的平面角.
例2 如图,在底面是直角梯形的四棱锥 ABCD中, 面ABCD, 求面SCD与面SBA所成二面角的正切值.
解:题设中已有“线面垂直”条件,只需找到棱,依据三垂线定理或逆定理条件得到二面角的平面角.
延长BA、CD相交于点E,连接SE,则SE是所求二面角的棱.
AD/BC,BC=2AD, EA=AB=SA,.. 得面SEB上面EBC,EB是交线,又BC上EB,BC上面SEB,SB是SC在面SEB上的射影,SC1SE,△BSC是所求二面角的平面角.
SB, 即所求二面角的正切值为
求法
3、辅助平面法
(1)求二面角 的大小,可转化为求β的拓展半平面与a所成二面角大小,取其邻补角即可,
(2)对于一些无棱二面角问题有时我们不必去找棱,而通过移面法去求另一个平面角相等的二面角.即把其中一个平面平行移动使之与另一半平面相交、形成一个新的有棱二面角,求出有棱二面角的度数即为无棱二面角度数.
例3.在正方体 中,求二面角 的大小.
略解:本题的常规解法是在半平面, 和 内构作二面角的平面角,但过程较繁、而利用半平面 的延伸面A;B,D解之,过程十分简洁.
作 ,垂足为E,连结A,E,. 是二面角 的平面角.
设正方体棱长为a,可得 即二面角 大小为 又二面角 与 C互为补角,二面角 大小为
求法
4、法向量法
环节四
学以致用
1.在正方体 中,
(1)求异面直线AB与 所成的角;
(2)求异面直线AB和 所成的角
2.等腰 的顶点A在平面α外底边BC在平面α内,已知底边长 腰长 又知点A到平面α的垂线段
(1)等腰 的高AE的长;
(2)斜线AE和平面α所成的角的大小(精确到1°).
15
42°
3.已知P为二面角 内一点,且P到两个半平面的距离都等于P到棱的距离的一半,则这个二面角的度数是多少
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
