北师大版数学八年级下册同步课件:6.4 第1课时 多边形的内角和(共13张PPT)
文档属性
| 名称 | 北师大版数学八年级下册同步课件:6.4 第1课时 多边形的内角和(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 203.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 17:11:30 | ||
图片预览




文档简介
(共13张PPT)
第六章 平行四边形
6.4 第1课时 多边形的内角和
知识回顾
问题1:你还记得三角形内角和是多少度吗?
三角形内角和 180°
都是360°
问题2:你知道长方形和正方形的内角和是多少度吗?
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?21*c
问题:
获取新知
A
C
D
E
B
A
C
D
E
B
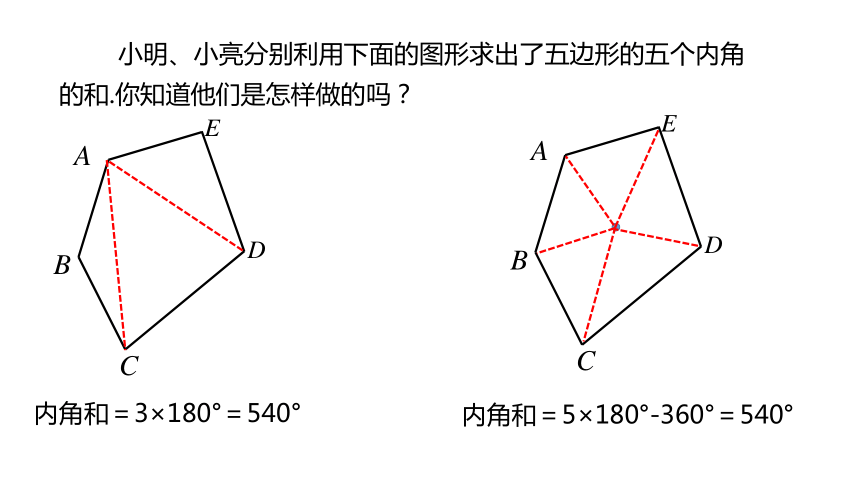
内角和=3×180°=540°
内角和=5×180°-360°=540°
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
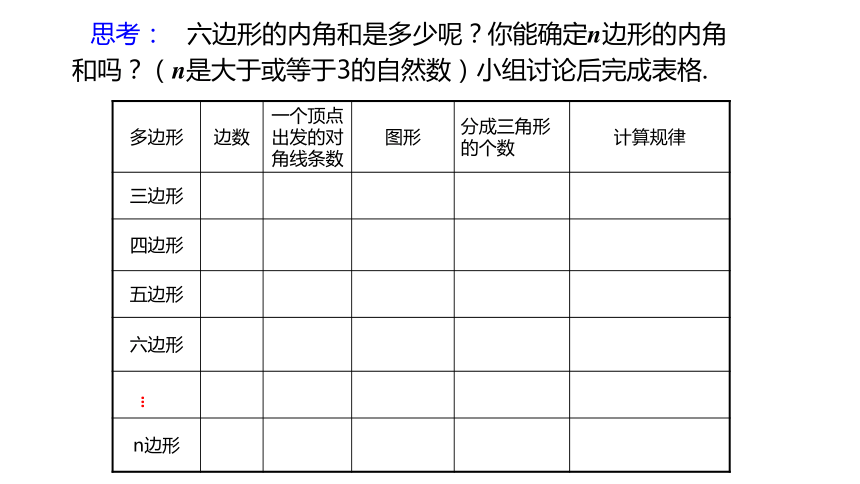
思考: 六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
总结归纳
一般地,从n边形的一个顶点出发,可以作_________
条对角线,它们将n边形分为__________个三角形,n边形
的内角和等于______________.
(n - 3)
(n - 2)
(n - 2)×180°
正n边形的每个内角的度数为
例题讲解
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B 与∠D有怎样的关系
解:∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
随堂演练
1. 内角和为540°的多边形是( )
C
2. 若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
B
3. 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
B
4. 如果两个多边形的边数之比为1∶2,这两个多边形的内角之和为1440°,请你确定这两个多边形的边数.
解:设这两个多边形的边数分别为n,2n.根据题意,得
(n-2)×180°+(2n-2)×180°=1440°,
解得n=4.所以2n=8.
故这两个多边形的边数分别为4和8.
课堂小结
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
正多
边形
内角=
第六章 平行四边形
6.4 第1课时 多边形的内角和
知识回顾
问题1:你还记得三角形内角和是多少度吗?
三角形内角和 180°
都是360°
问题2:你知道长方形和正方形的内角和是多少度吗?
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?21*c
问题:
获取新知
A
C
D
E
B
A
C
D
E
B
内角和=3×180°=540°
内角和=5×180°-360°=540°
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
思考: 六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
总结归纳
一般地,从n边形的一个顶点出发,可以作_________
条对角线,它们将n边形分为__________个三角形,n边形
的内角和等于______________.
(n - 3)
(n - 2)
(n - 2)×180°
正n边形的每个内角的度数为
例题讲解
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B 与∠D有怎样的关系
解:∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
随堂演练
1. 内角和为540°的多边形是( )
C
2. 若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
B
3. 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
B
4. 如果两个多边形的边数之比为1∶2,这两个多边形的内角之和为1440°,请你确定这两个多边形的边数.
解:设这两个多边形的边数分别为n,2n.根据题意,得
(n-2)×180°+(2n-2)×180°=1440°,
解得n=4.所以2n=8.
故这两个多边形的边数分别为4和8.
课堂小结
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
正多
边形
内角=
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
