人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试(含答案) | 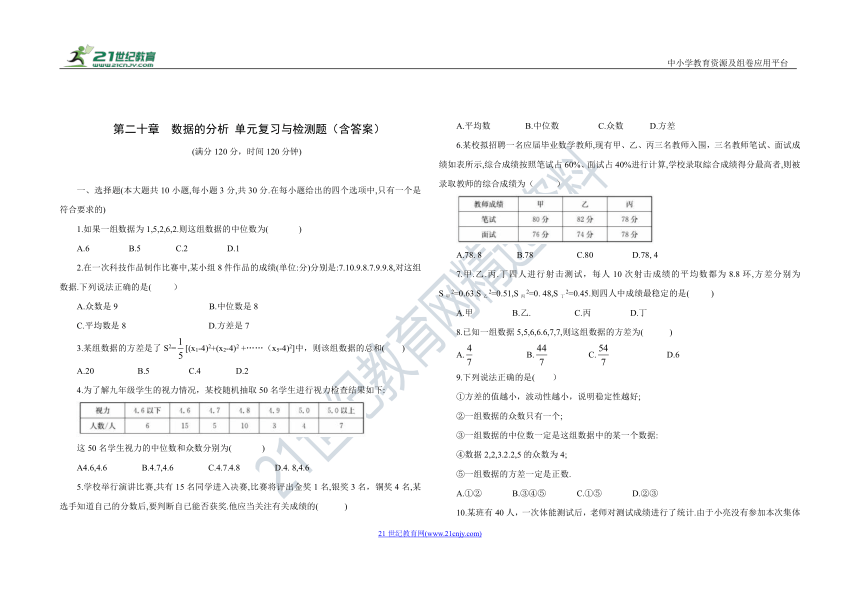 | |
| 格式 | zip | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 16:12:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十章 数据的分析 单元复习与检测题(含答案)
(满分120分,时间120分钟)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是符合要求的)
1.如果一组数据为1,5,2,6,2.则这组数据的中位数为( )
A.6 B.5 C.2 D.1
2.在一次科技作品制作比赛中,某小组8件作品的成绩(单位:分)分别是:7.10.9.8.7.9.9.8,对这组数据.下列说法正确的是( )
A.众数是9 B.中位数是8
C.平均数是8 D.方差是7
3.某组数据的方差是了S2=[(x1-4)2+(x2-4)2 +……(x5-4)2]中,则该组数据的总和( )
A.20 B.5 C.4 D.2
4.为了解九年级学生的视力情况,某校随机抽取50名学生进行视力检查结果如下:
这50名学生视力的中位数和众数分别为( )
A4.6,4.6 B.4.7,4.6 C.4.7.4.8 D.4. 8,4.6
5.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自已能否获奖.他应当关注有关成绩的( )
A.平均数 B.中位数 C.众数 D.方差
6.某校拟招聘一名应届毕业数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取綜合成绩得分最高者,则被录取教师的综合成绩为( )
A.78. 8 B.78 C.80 D.78, 4
7.甲.乙.丙.丁四人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为 S甲2=0.63.S乙2=0.51,S丙2=0. 48,S丁2=0.45.则四人中成绩最稳定的是( )
A.甲 B.乙. C.丙 D.丁
8.已知一组数据5,5,6,6.6,7,7,则这组数据的方差为( )
A. B. C. D.6
9.下列说法正确的是( )
①方差的值越小,波动性越小,说明稳定性越好;
②一组数据的众数只有一个;
③一组数据的中位数一定是这组数据中的某一个数据:
④数据2,2,3.2.2,5的众数为4;
⑤一组数据的方差一定是正数.
A.①② B.③④⑤ C.①⑤ D.②③
10.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.若一-组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分如果采访写作.计算机操作和创意设计的成绩按5:2:3计算,那么他的素质测试的最终成绩为
13.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物。也称可入肺颗粒物)指数如表,则该周PM2.5指数的众数和中位数分别是
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,那么另一组数据3x1-2,3x2- 2,3x3-2,3x4-2,3x5-2的平均数是
15.为了考察甲、乙两种小麦的长势,某农研所科技人员,分别从中随机抽取10株发苗,测得苗高(单位:cm)如下表:
则 种小麦的长势比较整齐. (选填“甲”或“乙”)
16.某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下:
由此你能给这家鞋店提供的进货建议是
17.某校组织学生参加了植树活动,八年级甲班52名学生每人植树情况统计如下表:
那么这52名学生植树情况的众数是
18.某校八年级共有三个班级,在一次数学考试中,各班人数及其平均分统计如下,则此次考试八年级数学平均分为______分。
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19. (8分)如果一组数据3,2,2,4,x的平均数为3.
(1)求x的值;
(2)求这组数据的众数.
20. (9分)某校八年级师生为了响应“绿水青山就是金山银山”的号召,在今年3月的植树月活动中到某荒山植树.如图是抽查了其中20名师生植树棵数的统计图。
(1)求这20名师生种树棵数的平均数、众数、中位数;
(2)如果该校八年级共有师生500名,所植树的存活率是90% .估计所植的树共有多少棵存活
21. (9分)为了考察包装机包装糖果质量的稳定性,从中抽取了10袋,测得它们的实际质量(单位:g)如下:505 ,504, 505, 498, 505, 502 , 507 ,505, 503,506.
(1)求平均每袋的质量是多少克;
(2)求样本的方差.
22.(10分)某公司招聘职员,对甲.乙两位候选人进行了面试,面试中包括形体、口才、专业知识.他们的成绩(百分制)如下表:
(1)如果公司根据经营性质和岗位要求,以面试成绩中形体、口才、专业知识按照2: 4 : 4的比值确定成绩,请计算甲、乙两人各自的平均成绩,看看谁将被录取
(2)如果公司根据经营性质和岗位要求,以面试成绩中形体占30%,口才占20%,专业知识占50%确定成绩,那么你认为该公司应该录取谁
23.(10分)某中学八年级举行跳绳比赛.要求每班选出5名学生参加,在规定时间每人跳绳不低于150次为优秀,冠、亚军在八(1)、八(5)两班中产生.下表是这两个班的5名学生的比赛数据(单位:次):
根据以上信息,解答下列问题:
(1)求两班的优秀率及两班数据的中位数;
(2)请你从优秀率.中位数和方差三方面进行简要分析,确定获冠军奖的班级.
24.(12分)某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
(1)根据以上数据.将下面两个表格补充完整:
王方10次射箭得分情况:
李明10次射箭得分情况:
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,选派谁参加比赛合适。
第20章测试题 参考答案
1.C 2.A 3.A 4.B 5.B 6.A 7.D 8.A 9.C 10.B.
11.4.5 12.71 分 13. 150,155 14.4 15. 乙
16.25.5 cm尺码型号的鞋子可以多进一些
17.6 18.91
19.解:(1)由题意知,数据3,2,2,4,x的平均数为3,则(3+2+2+4+x)=3X5,x=4;
(2)这组数据中2和4均出现了2次,并列最多,所以众数为2和4.
20.解:(1)这20名师生种树棵数的平均数是
(2X4+3X6+4X8+5X2)=3.4;
这组数据的众数是4;
把这些数从小到大排列,中位数是第10、11 个数的平均数,则中住数是3.5;
(2)根据题意得3. 4X90%X500=1 530(棵)。
即估计所植的树共有1 530棵存活。
21.解:(1)平均每袋的质量是X (505 +504+ 505+ 498+505+502 +507 + 505 + 503 + 506)= 504(g) ;
(2)方差为X[(505 - 504)2+ (504 - 504)2 + (505一504)2+ (498- 504)2 + (505- 504)2+ (502- 504)2 +(507-504)2+ (505 - 504)2+ (503 - 504)2 + (506一504)2]=5.8.
22.解:(1)甲的平均成绩:84(分),
己的平均成绩:82(分),
因为84>82,所以公司将录取甲;
(2)甲的平均成绩:
80X30%+ 80X20% +90X50%=24+ 16+45=85(分),
己的平均成绩:
90X30% + 70X20% +90X50%=27+14+45= 86(分),
因为85<86,所以公司将录取乙。
23.解:(1)入(1)班的优秀率为x 100% = 60%,
八(2)班的优秀率为X 100%= 40%;
因为八(1)班成绩由低到高排列为139、148、150、153、160,
八(2)班成绩由低到高排列为139、145、147、150、169.
所以八(1)班成绩的中位数为150,八(2)班成绩的中位数为147;
(2)入(1)班获冠军奖.
理由:从优秀率看,入(1)班的优秀人数多;
从中位数看,八(1)班较大,一般水平较高;
从方差看,八(1)班的成绩比八(2)班的稳定,
所以八(1)班获冠军奖.
24.解:(1)王方10次射箭得分情况:
李明10次射箭得分情况:
(2)王方的平均数=(6+14+8+ 27+ 30)= 8.5;
李明的平均数=(48+27+10)=8.5;
(3)因为S2王方=[(6-8.5)2 +2(7-8.5)2+(8-8.5)2+3(9-8.5)2+3(10-8.5)2]=1.85,
S2李明=[6(8-8.5)2+3(9-8.5)2+(10-8.5)2]=0.45,
所以选派李明参加比赛合适。
21世纪教育网(www.21cnjy.com)
第二十章 数据的分析 单元复习与检测题(含答案)
(满分120分,时间120分钟)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是符合要求的)
1.如果一组数据为1,5,2,6,2.则这组数据的中位数为( )
A.6 B.5 C.2 D.1
2.在一次科技作品制作比赛中,某小组8件作品的成绩(单位:分)分别是:7.10.9.8.7.9.9.8,对这组数据.下列说法正确的是( )
A.众数是9 B.中位数是8
C.平均数是8 D.方差是7
3.某组数据的方差是了S2=[(x1-4)2+(x2-4)2 +……(x5-4)2]中,则该组数据的总和( )
A.20 B.5 C.4 D.2
4.为了解九年级学生的视力情况,某校随机抽取50名学生进行视力检查结果如下:
这50名学生视力的中位数和众数分别为( )
A4.6,4.6 B.4.7,4.6 C.4.7.4.8 D.4. 8,4.6
5.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自已能否获奖.他应当关注有关成绩的( )
A.平均数 B.中位数 C.众数 D.方差
6.某校拟招聘一名应届毕业数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取綜合成绩得分最高者,则被录取教师的综合成绩为( )
A.78. 8 B.78 C.80 D.78, 4
7.甲.乙.丙.丁四人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为 S甲2=0.63.S乙2=0.51,S丙2=0. 48,S丁2=0.45.则四人中成绩最稳定的是( )
A.甲 B.乙. C.丙 D.丁
8.已知一组数据5,5,6,6.6,7,7,则这组数据的方差为( )
A. B. C. D.6
9.下列说法正确的是( )
①方差的值越小,波动性越小,说明稳定性越好;
②一组数据的众数只有一个;
③一组数据的中位数一定是这组数据中的某一个数据:
④数据2,2,3.2.2,5的众数为4;
⑤一组数据的方差一定是正数.
A.①② B.③④⑤ C.①⑤ D.②③
10.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.若一-组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分如果采访写作.计算机操作和创意设计的成绩按5:2:3计算,那么他的素质测试的最终成绩为
13.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物。也称可入肺颗粒物)指数如表,则该周PM2.5指数的众数和中位数分别是
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,那么另一组数据3x1-2,3x2- 2,3x3-2,3x4-2,3x5-2的平均数是
15.为了考察甲、乙两种小麦的长势,某农研所科技人员,分别从中随机抽取10株发苗,测得苗高(单位:cm)如下表:
则 种小麦的长势比较整齐. (选填“甲”或“乙”)
16.某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下:
由此你能给这家鞋店提供的进货建议是
17.某校组织学生参加了植树活动,八年级甲班52名学生每人植树情况统计如下表:
那么这52名学生植树情况的众数是
18.某校八年级共有三个班级,在一次数学考试中,各班人数及其平均分统计如下,则此次考试八年级数学平均分为______分。
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19. (8分)如果一组数据3,2,2,4,x的平均数为3.
(1)求x的值;
(2)求这组数据的众数.
20. (9分)某校八年级师生为了响应“绿水青山就是金山银山”的号召,在今年3月的植树月活动中到某荒山植树.如图是抽查了其中20名师生植树棵数的统计图。
(1)求这20名师生种树棵数的平均数、众数、中位数;
(2)如果该校八年级共有师生500名,所植树的存活率是90% .估计所植的树共有多少棵存活
21. (9分)为了考察包装机包装糖果质量的稳定性,从中抽取了10袋,测得它们的实际质量(单位:g)如下:505 ,504, 505, 498, 505, 502 , 507 ,505, 503,506.
(1)求平均每袋的质量是多少克;
(2)求样本的方差.
22.(10分)某公司招聘职员,对甲.乙两位候选人进行了面试,面试中包括形体、口才、专业知识.他们的成绩(百分制)如下表:
(1)如果公司根据经营性质和岗位要求,以面试成绩中形体、口才、专业知识按照2: 4 : 4的比值确定成绩,请计算甲、乙两人各自的平均成绩,看看谁将被录取
(2)如果公司根据经营性质和岗位要求,以面试成绩中形体占30%,口才占20%,专业知识占50%确定成绩,那么你认为该公司应该录取谁
23.(10分)某中学八年级举行跳绳比赛.要求每班选出5名学生参加,在规定时间每人跳绳不低于150次为优秀,冠、亚军在八(1)、八(5)两班中产生.下表是这两个班的5名学生的比赛数据(单位:次):
根据以上信息,解答下列问题:
(1)求两班的优秀率及两班数据的中位数;
(2)请你从优秀率.中位数和方差三方面进行简要分析,确定获冠军奖的班级.
24.(12分)某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
(1)根据以上数据.将下面两个表格补充完整:
王方10次射箭得分情况:
李明10次射箭得分情况:
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,选派谁参加比赛合适。
第20章测试题 参考答案
1.C 2.A 3.A 4.B 5.B 6.A 7.D 8.A 9.C 10.B.
11.4.5 12.71 分 13. 150,155 14.4 15. 乙
16.25.5 cm尺码型号的鞋子可以多进一些
17.6 18.91
19.解:(1)由题意知,数据3,2,2,4,x的平均数为3,则(3+2+2+4+x)=3X5,x=4;
(2)这组数据中2和4均出现了2次,并列最多,所以众数为2和4.
20.解:(1)这20名师生种树棵数的平均数是
(2X4+3X6+4X8+5X2)=3.4;
这组数据的众数是4;
把这些数从小到大排列,中位数是第10、11 个数的平均数,则中住数是3.5;
(2)根据题意得3. 4X90%X500=1 530(棵)。
即估计所植的树共有1 530棵存活。
21.解:(1)平均每袋的质量是X (505 +504+ 505+ 498+505+502 +507 + 505 + 503 + 506)= 504(g) ;
(2)方差为X[(505 - 504)2+ (504 - 504)2 + (505一504)2+ (498- 504)2 + (505- 504)2+ (502- 504)2 +(507-504)2+ (505 - 504)2+ (503 - 504)2 + (506一504)2]=5.8.
22.解:(1)甲的平均成绩:84(分),
己的平均成绩:82(分),
因为84>82,所以公司将录取甲;
(2)甲的平均成绩:
80X30%+ 80X20% +90X50%=24+ 16+45=85(分),
己的平均成绩:
90X30% + 70X20% +90X50%=27+14+45= 86(分),
因为85<86,所以公司将录取乙。
23.解:(1)入(1)班的优秀率为x 100% = 60%,
八(2)班的优秀率为X 100%= 40%;
因为八(1)班成绩由低到高排列为139、148、150、153、160,
八(2)班成绩由低到高排列为139、145、147、150、169.
所以八(1)班成绩的中位数为150,八(2)班成绩的中位数为147;
(2)入(1)班获冠军奖.
理由:从优秀率看,入(1)班的优秀人数多;
从中位数看,八(1)班较大,一般水平较高;
从方差看,八(1)班的成绩比八(2)班的稳定,
所以八(1)班获冠军奖.
24.解:(1)王方10次射箭得分情况:
李明10次射箭得分情况:
(2)王方的平均数=(6+14+8+ 27+ 30)= 8.5;
李明的平均数=(48+27+10)=8.5;
(3)因为S2王方=[(6-8.5)2 +2(7-8.5)2+(8-8.5)2+3(9-8.5)2+3(10-8.5)2]=1.85,
S2李明=[6(8-8.5)2+3(9-8.5)2+(10-8.5)2]=0.45,
所以选派李明参加比赛合适。
21世纪教育网(www.21cnjy.com)
