人教版数学二年级下册 第3单元第1课时《认识轴对称图形、平移和旋转》教案
文档属性
| 名称 | 人教版数学二年级下册 第3单元第1课时《认识轴对称图形、平移和旋转》教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 00:00:00 | ||
图片预览

文档简介
第1课时 认识轴对称图形、平移和旋转
备教材内容
1.本课时学习的是教材28~31页例1、例2、例3及相关习题。
2.例1以动态操作的方式,教学轴对称图形。例2教学图形的平移。例3呈现了风车、旋转小飞机、直升机螺旋桨的转动,让学生通过观察发现它们运动的共同点:物体的每个部分都绕同一个点或轴转动,从而认识旋转现象。
3.本课时通过剪一剪、移一移、看一看等活动,让学生在实际生活中发现并理解图形的运动,感受数学和生活的密切联系,既为学生进一步学习抽象的图形运动知识积累感性认识,又为今后从图形运动的角度认识图形(如圆柱、圆锥)、理解度量(平行四边形、三角形面积的推导等)作铺垫,同时逐步培养学生的空间想象力。
备已学知识
生活中的相关现象
备教学目标
知识与技能
1.借助生活中的对称现象,通过观察操作,使学生直观地认识轴对称图形。
2.通过观察操作,初步理解图形的平移,能辨认简单图形平移后的图形。
3.借助日常生活中的旋转现象,通过观察操作,使学生初步理解旋转。
过程与方法
经历剪一剪、移一移、看一看等过程,培养观察能力、想象能力和语言表达能力,发展初步的空间观念。
情感、态度与价值观
1.在认识、制作和欣赏轴对称图形的过程中,感受物体或图形的对称美,体会学习数学的乐趣。
2.在探究和交流活动中,初步形成空间观念,感受数学与生活的密切联系。
备重点难点
重点:认识平移、旋转现象及轴对称图形的基本特征,能准确判断生活中的轴对称图形。
难点:能找出轴对称图形的对称轴,能根据平移或旋转的特征解决相关问题。
备知识讲解
知识点一 对称现象及轴对称图形(认识)
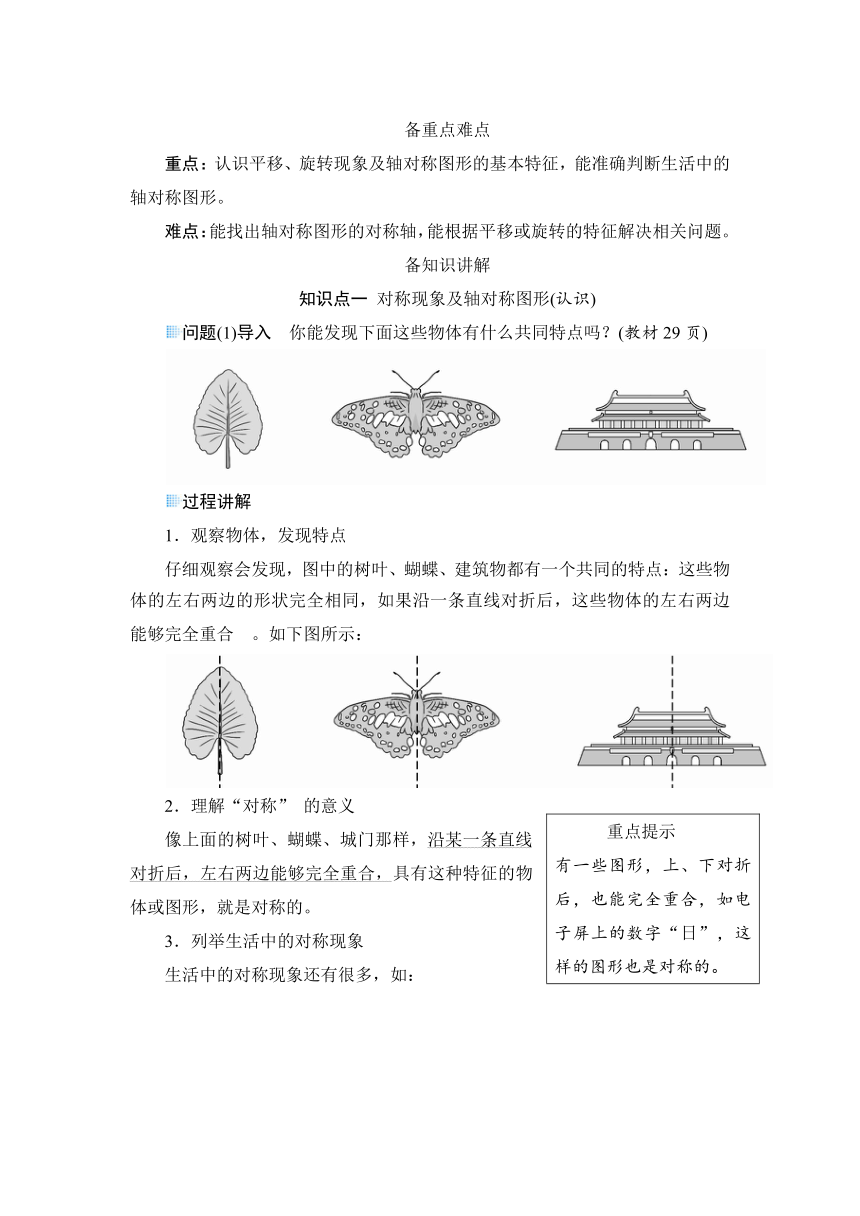
问题(1)导入 你能发现下面这些物体有什么共同特点吗?(教材29页)
过程讲解
1.观察物体,发现特点
仔细观察会发现,图中的树叶、蝴蝶、建筑物都有一个共同的特点:这些物体的左右两边的形状完全相同,如果沿一条直线对折后,这些物体的左右两边 能够完全重合 。如下图所示:
重点提示 有一些图形,上、下对折后,也能完全重合,如电子屏上的数字“日”,这样的图形也是对称的。
2.理解“对称” 的意义
像上面的树叶、蝴蝶、城门那样,沿某一条直线对折后,左右两边能够完全重合,具有这种特征的物体或图形,就是对称的。
3.列举生活中的对称现象
生活中的对称现象还有很多,如:
……
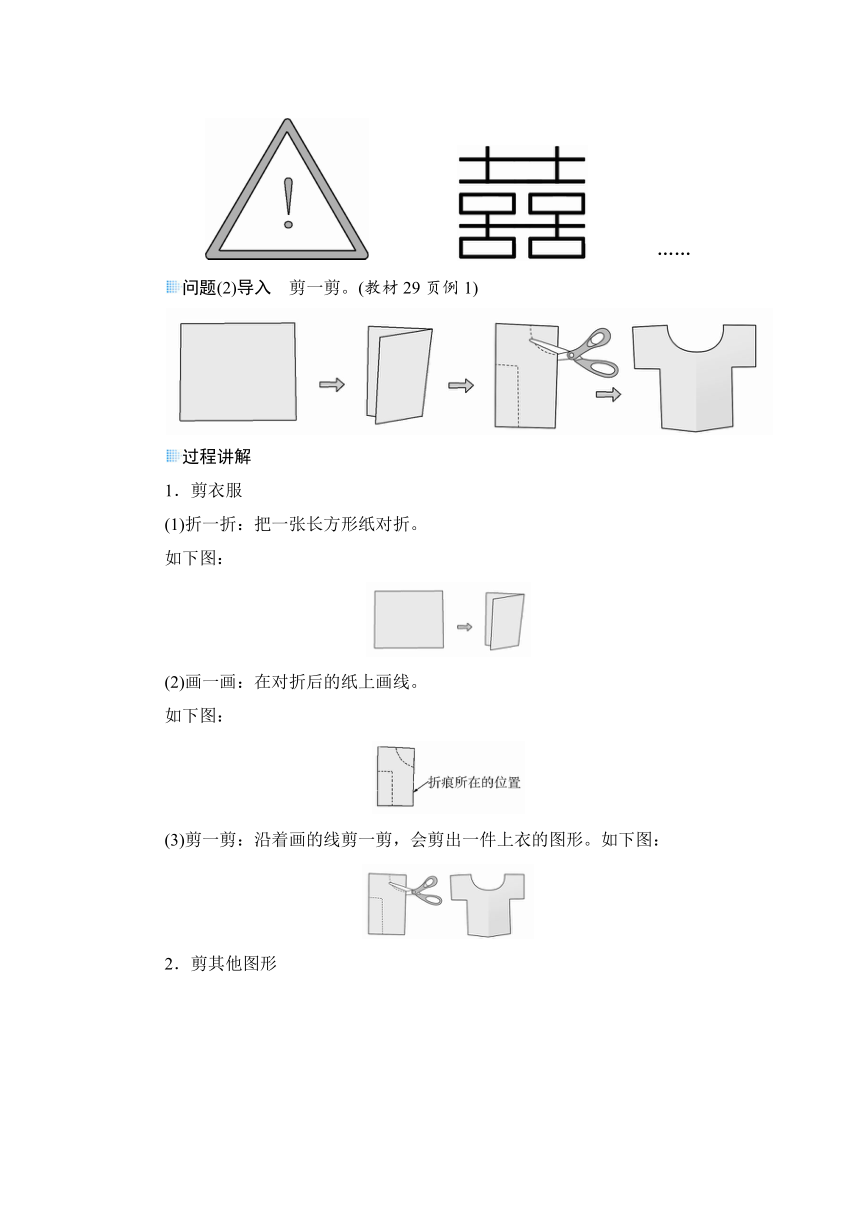
问题(2)导入 剪一剪。(教材29页例1)
过程讲解
1.剪衣服
(1)折一折:把一张长方形纸对折。
如下图:
(2)画一画:在对折后的纸上画线。
如下图:
(3)剪一剪:沿着画的线剪一剪,会剪出一件上衣的图形。如下图:
2.剪其他图形
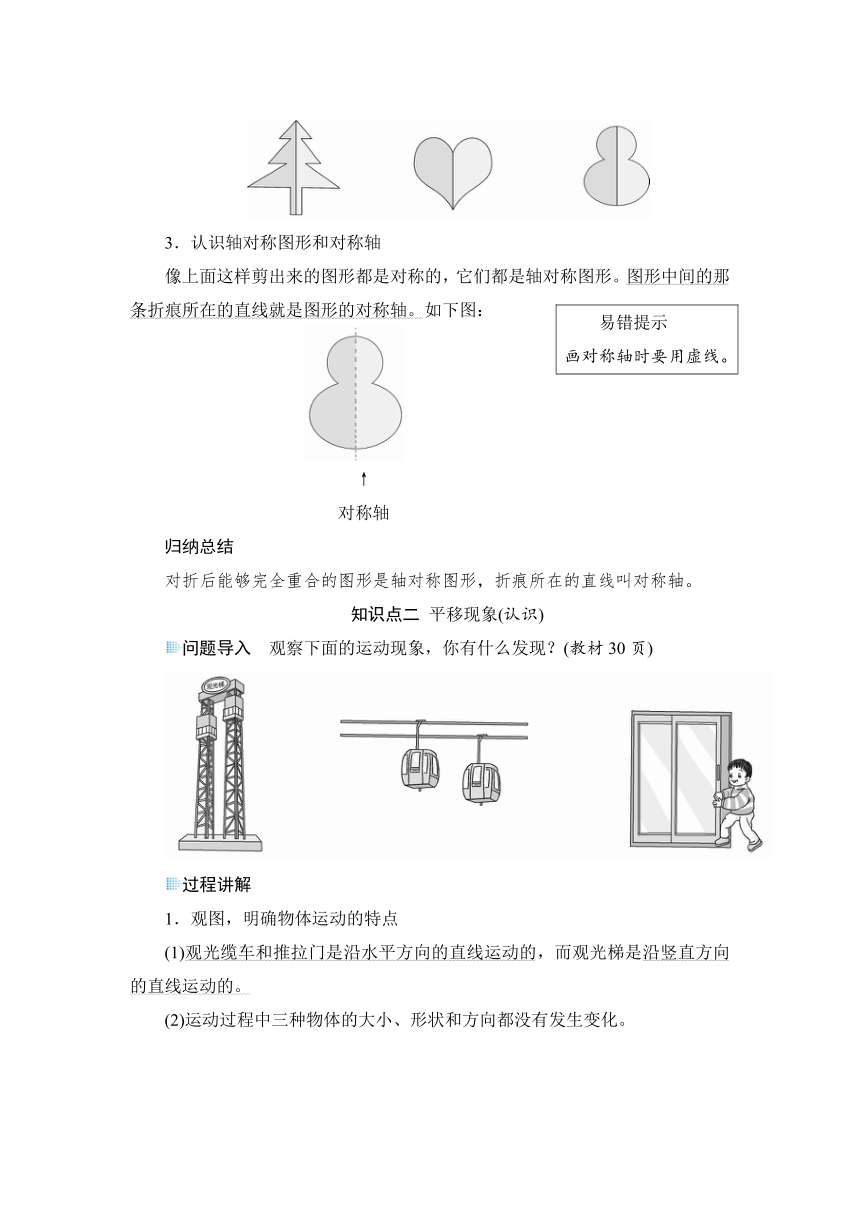
3.认识轴对称图形和对称轴
易错提示 画对称轴时要用虚线。
像上面这样剪出来的图形都是对称的,它们都是轴对称图形。图形中间的那条折痕所在的直线就是图形的对称轴。如下图:
↑
对称轴
归纳总结
对折后能够完全重合的图形是轴对称图形,折痕所在的直线叫对称轴。
知识点二 平移现象(认识)
问题导入 观察下面的运动现象,你有什么发现?(教材30页)
过程讲解
1.观图,明确物体运动的特点
(1)观光缆车和推拉门是沿水平方向的直线运动的,而观光梯是沿竖直方向的直线运动的。
(2)运动过程中三种物体的大小、形状和方向都没有发生变化。
难点点拨 物体做平移运动时,物体的位置发生改变,但物体本身的大小、形状和方向不发生改变。
(3)三种物体的位置都发生了变化。
2.明确“平移”的意义
像推拉门、观光缆车和观光梯那样,无论是沿水平方向的直线运动,还是沿竖直方向的直线运动,在运动过程中,物体本身的方向不发生改变,把这种运动现象称为平移。
3.列举生活中的平移现象
生活中的平移现象有很多,例如:火车站、飞机场运送行李的传送带上行李的移动;电视机在流水线上的移动;电梯的上升、下降;抽屉的推和拉……
归纳总结
物体或图形沿直线运动,而本身的大小、形状和方向不发生改变时,这种运动现象就是平移。
知识点三 通过平移能够相互重合的图形的特点(掌握运用)
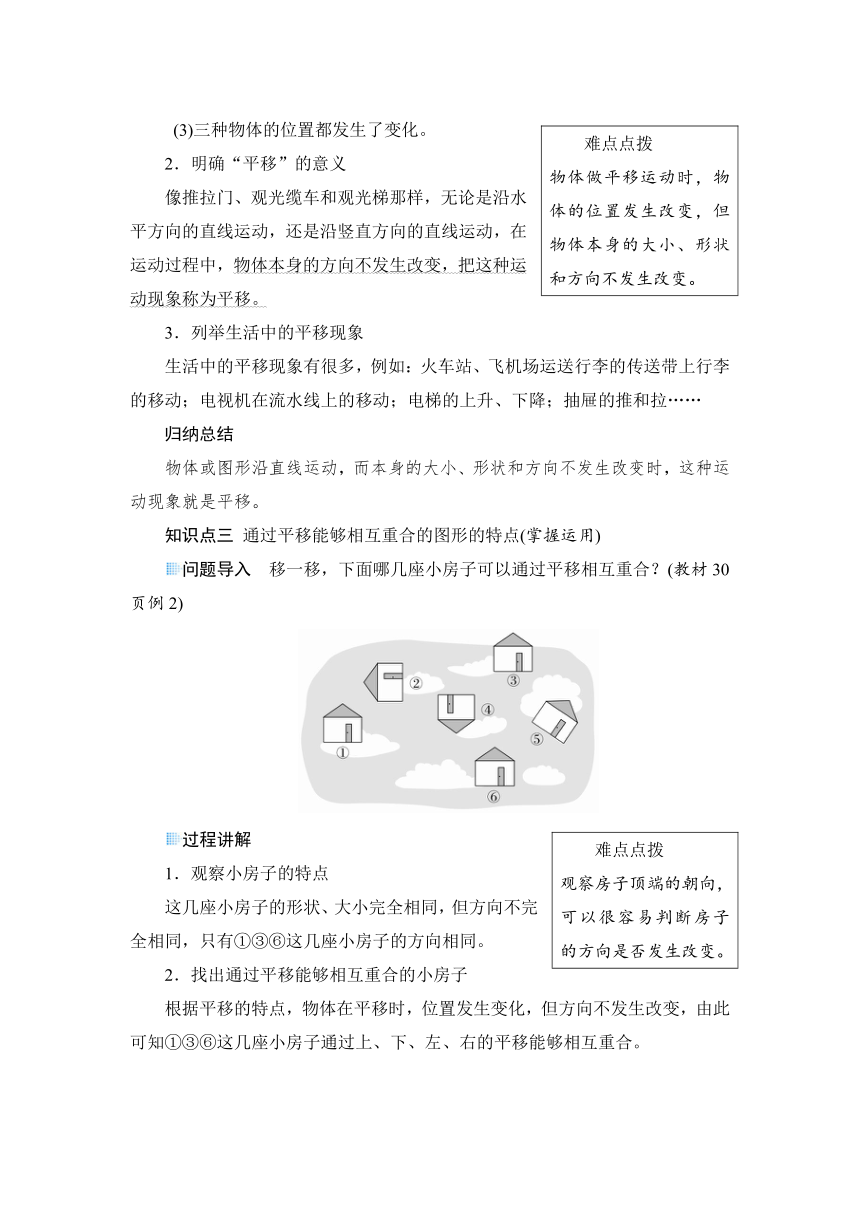
问题导入 移一移,下面哪几座小房子可以通过平移相互重合?(教材30页例2)
难点点拨 观察房子顶端的朝向,可以很容易判断房子的方向是否发生改变。
过程讲解
1.观察小房子的特点
这几座小房子的形状、大小完全相同,但方向不完全相同,只有①③⑥这几座小房子的方向相同。
2.找出通过平移能够相互重合的小房子
根据平移的特点,物体在平移时,位置发生变化,但方向不发生改变,由此可知①③⑥这几座小房子通过上、下、左、右的平移能够相互重合。
归纳总结
只有形状、大小、方向完全相同的图形通过平移才能够相互重合。
知识点四 旋转现象(认识)
问题导入 观察下面的运动现象,你有什么发现?(教材31页例3)
过程讲解
1.观图,明确物体运动的特点
风车、旋转小飞机和直升机螺旋桨的转动,都是绕着同一个点或轴来做圆周运动的。
2.明确“旋转”的意义
像上面这样,物体绕着一个点或轴进行圆周运动的现象就是旋转。
3.列举生活中的旋转现象
生活中的旋转现象有很多,例如:钟表上指针的转动;电风扇扇叶的转动;司机开车时方向盘的转动……
归纳总结
物体绕着一个点或轴进行圆周运动的现象就是旋转。
备易错易混
误区一 下面是轴对称图形的有(①②④⑤)。
错解分析 此题错在对⑤号图形判断错误。⑤号图形是平行四边形,对折后,折痕两侧的部分不能完全重合,它不属于轴对称图形。
错解改正 ①②④
温馨提示 平行四边形不属于轴对称图形。
误区二 判断:图形不是轴对称图形。(√)
错解分析 此题错在不理解轴对称图形的意义。图形沿中间的虚线上下对折,两边能够完全重合,是轴对称图形。
错解改正 ×
温馨提示 判断一个图形是不是轴对称图形,可分别从不同的位置对折,只要有一种情况能完全重合,就可判断其为轴对称图形。
误区三 填空:汽车车轮的转动是(平移)现象。
错解分析 此题错在没有正确区分平移和旋转现象。物体做平移运动时,自身方向不发生改变。汽车车轮是绕着轴心做圆周运动的,因此是旋转现象。
错解改正 旋转
温馨提示 汽车在笔直的公路上行驶是平移现象,而汽车车轮的转动是旋转现象。
误区四 判断:风车转动10圈后变小了。(√)
错解分析 此题错在没有掌握旋转的特征。无论风车转动多少圈,它的大小都不会发生改变。
错解改正 ×
温馨提示 物体在做旋转运动时,形状、大小都不会改变。
备综合能力
能力点一 运用观察法与分析法解决对称轴数量问题
典型例题 下面的轴对称图形各有几条对称轴?
思路分析 第一个图形是由上、下2个大小相同的圆组成的,可以横着画1条对称轴,也可以竖着画1条对称轴,因此它有2条对称轴,如右图。
第二个图形是由3个大小相同的圆组成的,把其中任意1个圆的中心和另外2个圆的中心连接处相连并延长,都可以画出对称轴,因此它有3条对称轴,如右图。
正确解答 2 3
方法提示 有些轴对称图形的对称轴不止1条,做题时,要仔细观察、认真思考。
能力点二 运用观察法解决图形旋转的问题
典型例题 神奇的转盘。
(1)猫转动( )格就可以转到老鼠现在的位置。
(2)当蜗牛转到猫现在的位置时,熊猫转到( )现在的位置上,老鼠转到( )现在的位置上。
思路分析 (1)首先要确定猫现在的位置到老鼠现在的位置有几格,数格子时应从猫前面的一格数起,数到老鼠现在的位置结束。
(2)如右图,蜗牛转到猫现在的位置时,转动了4格,再看熊猫转动4格后所到的位置,老鼠转动4格后所到的位置。
正确解答 (1)4 (2)蜗牛 狮子
方法总结 解决旋转了几格的问题,关键是把格数数准确,数格子时,应从起始格前面的一格数起。
备教学资料
生活中的轴对称图形
常见的图形中,线段和角都是轴对称图形,线段的垂直平分线就是它的对称轴,角的对称轴就是角平分线所在的直线。此外,等腰三角形、等腰梯形、长方形(包括正方形)、圆等也都是轴对称图形。其中圆的任意一条直径所在的直线,都是它的对称轴,因此圆有无数条对称轴。(如下图)
轴对称与轴对称图形
两个图形,如果把其中一个图形沿着某一条直线对折,能与另一个图形完全重合,我们就说这两个图形成轴对称,又称这两个图形关于该直线对称。这条直线就是对称轴,两个图形中的对应点叫做关于这条直线的对称点。
一个图形,如果沿一条直线对折, 直线两侧的部分能够完全重合, 那么这个图形就叫做轴对称图形。这条直线就是它的对称轴。(具体如下)
轴对称图形 轴对称
图形
区别 (1)轴对称图形是指一个具有特殊形状的图形,只对一个图形而言。 (2)对称轴不一定只有一条。 (1)轴对称是指两个图形的位置关系,必须涉及两个图形。 (2)只有一条对称轴。
联系 如果把轴对称图形沿对称轴分成两部分,那么这两部分就关于这条直线成轴对称。 如果把两个成轴对称的图形拼在一起看成一个整体,那么它就是一个轴对称图形。
备教材内容
1.本课时学习的是教材28~31页例1、例2、例3及相关习题。
2.例1以动态操作的方式,教学轴对称图形。例2教学图形的平移。例3呈现了风车、旋转小飞机、直升机螺旋桨的转动,让学生通过观察发现它们运动的共同点:物体的每个部分都绕同一个点或轴转动,从而认识旋转现象。
3.本课时通过剪一剪、移一移、看一看等活动,让学生在实际生活中发现并理解图形的运动,感受数学和生活的密切联系,既为学生进一步学习抽象的图形运动知识积累感性认识,又为今后从图形运动的角度认识图形(如圆柱、圆锥)、理解度量(平行四边形、三角形面积的推导等)作铺垫,同时逐步培养学生的空间想象力。
备已学知识
生活中的相关现象
备教学目标
知识与技能
1.借助生活中的对称现象,通过观察操作,使学生直观地认识轴对称图形。
2.通过观察操作,初步理解图形的平移,能辨认简单图形平移后的图形。
3.借助日常生活中的旋转现象,通过观察操作,使学生初步理解旋转。
过程与方法
经历剪一剪、移一移、看一看等过程,培养观察能力、想象能力和语言表达能力,发展初步的空间观念。
情感、态度与价值观
1.在认识、制作和欣赏轴对称图形的过程中,感受物体或图形的对称美,体会学习数学的乐趣。
2.在探究和交流活动中,初步形成空间观念,感受数学与生活的密切联系。
备重点难点
重点:认识平移、旋转现象及轴对称图形的基本特征,能准确判断生活中的轴对称图形。
难点:能找出轴对称图形的对称轴,能根据平移或旋转的特征解决相关问题。
备知识讲解
知识点一 对称现象及轴对称图形(认识)
问题(1)导入 你能发现下面这些物体有什么共同特点吗?(教材29页)
过程讲解
1.观察物体,发现特点
仔细观察会发现,图中的树叶、蝴蝶、建筑物都有一个共同的特点:这些物体的左右两边的形状完全相同,如果沿一条直线对折后,这些物体的左右两边 能够完全重合 。如下图所示:
重点提示 有一些图形,上、下对折后,也能完全重合,如电子屏上的数字“日”,这样的图形也是对称的。
2.理解“对称” 的意义
像上面的树叶、蝴蝶、城门那样,沿某一条直线对折后,左右两边能够完全重合,具有这种特征的物体或图形,就是对称的。
3.列举生活中的对称现象
生活中的对称现象还有很多,如:
……
问题(2)导入 剪一剪。(教材29页例1)
过程讲解
1.剪衣服
(1)折一折:把一张长方形纸对折。
如下图:
(2)画一画:在对折后的纸上画线。
如下图:
(3)剪一剪:沿着画的线剪一剪,会剪出一件上衣的图形。如下图:
2.剪其他图形
3.认识轴对称图形和对称轴
易错提示 画对称轴时要用虚线。
像上面这样剪出来的图形都是对称的,它们都是轴对称图形。图形中间的那条折痕所在的直线就是图形的对称轴。如下图:
↑
对称轴
归纳总结
对折后能够完全重合的图形是轴对称图形,折痕所在的直线叫对称轴。
知识点二 平移现象(认识)
问题导入 观察下面的运动现象,你有什么发现?(教材30页)
过程讲解
1.观图,明确物体运动的特点
(1)观光缆车和推拉门是沿水平方向的直线运动的,而观光梯是沿竖直方向的直线运动的。
(2)运动过程中三种物体的大小、形状和方向都没有发生变化。
难点点拨 物体做平移运动时,物体的位置发生改变,但物体本身的大小、形状和方向不发生改变。
(3)三种物体的位置都发生了变化。
2.明确“平移”的意义
像推拉门、观光缆车和观光梯那样,无论是沿水平方向的直线运动,还是沿竖直方向的直线运动,在运动过程中,物体本身的方向不发生改变,把这种运动现象称为平移。
3.列举生活中的平移现象
生活中的平移现象有很多,例如:火车站、飞机场运送行李的传送带上行李的移动;电视机在流水线上的移动;电梯的上升、下降;抽屉的推和拉……
归纳总结
物体或图形沿直线运动,而本身的大小、形状和方向不发生改变时,这种运动现象就是平移。
知识点三 通过平移能够相互重合的图形的特点(掌握运用)
问题导入 移一移,下面哪几座小房子可以通过平移相互重合?(教材30页例2)
难点点拨 观察房子顶端的朝向,可以很容易判断房子的方向是否发生改变。
过程讲解
1.观察小房子的特点
这几座小房子的形状、大小完全相同,但方向不完全相同,只有①③⑥这几座小房子的方向相同。
2.找出通过平移能够相互重合的小房子
根据平移的特点,物体在平移时,位置发生变化,但方向不发生改变,由此可知①③⑥这几座小房子通过上、下、左、右的平移能够相互重合。
归纳总结
只有形状、大小、方向完全相同的图形通过平移才能够相互重合。
知识点四 旋转现象(认识)
问题导入 观察下面的运动现象,你有什么发现?(教材31页例3)
过程讲解
1.观图,明确物体运动的特点
风车、旋转小飞机和直升机螺旋桨的转动,都是绕着同一个点或轴来做圆周运动的。
2.明确“旋转”的意义
像上面这样,物体绕着一个点或轴进行圆周运动的现象就是旋转。
3.列举生活中的旋转现象
生活中的旋转现象有很多,例如:钟表上指针的转动;电风扇扇叶的转动;司机开车时方向盘的转动……
归纳总结
物体绕着一个点或轴进行圆周运动的现象就是旋转。
备易错易混
误区一 下面是轴对称图形的有(①②④⑤)。
错解分析 此题错在对⑤号图形判断错误。⑤号图形是平行四边形,对折后,折痕两侧的部分不能完全重合,它不属于轴对称图形。
错解改正 ①②④
温馨提示 平行四边形不属于轴对称图形。
误区二 判断:图形不是轴对称图形。(√)
错解分析 此题错在不理解轴对称图形的意义。图形沿中间的虚线上下对折,两边能够完全重合,是轴对称图形。
错解改正 ×
温馨提示 判断一个图形是不是轴对称图形,可分别从不同的位置对折,只要有一种情况能完全重合,就可判断其为轴对称图形。
误区三 填空:汽车车轮的转动是(平移)现象。
错解分析 此题错在没有正确区分平移和旋转现象。物体做平移运动时,自身方向不发生改变。汽车车轮是绕着轴心做圆周运动的,因此是旋转现象。
错解改正 旋转
温馨提示 汽车在笔直的公路上行驶是平移现象,而汽车车轮的转动是旋转现象。
误区四 判断:风车转动10圈后变小了。(√)
错解分析 此题错在没有掌握旋转的特征。无论风车转动多少圈,它的大小都不会发生改变。
错解改正 ×
温馨提示 物体在做旋转运动时,形状、大小都不会改变。
备综合能力
能力点一 运用观察法与分析法解决对称轴数量问题
典型例题 下面的轴对称图形各有几条对称轴?
思路分析 第一个图形是由上、下2个大小相同的圆组成的,可以横着画1条对称轴,也可以竖着画1条对称轴,因此它有2条对称轴,如右图。
第二个图形是由3个大小相同的圆组成的,把其中任意1个圆的中心和另外2个圆的中心连接处相连并延长,都可以画出对称轴,因此它有3条对称轴,如右图。
正确解答 2 3
方法提示 有些轴对称图形的对称轴不止1条,做题时,要仔细观察、认真思考。
能力点二 运用观察法解决图形旋转的问题
典型例题 神奇的转盘。
(1)猫转动( )格就可以转到老鼠现在的位置。
(2)当蜗牛转到猫现在的位置时,熊猫转到( )现在的位置上,老鼠转到( )现在的位置上。
思路分析 (1)首先要确定猫现在的位置到老鼠现在的位置有几格,数格子时应从猫前面的一格数起,数到老鼠现在的位置结束。
(2)如右图,蜗牛转到猫现在的位置时,转动了4格,再看熊猫转动4格后所到的位置,老鼠转动4格后所到的位置。
正确解答 (1)4 (2)蜗牛 狮子
方法总结 解决旋转了几格的问题,关键是把格数数准确,数格子时,应从起始格前面的一格数起。
备教学资料
生活中的轴对称图形
常见的图形中,线段和角都是轴对称图形,线段的垂直平分线就是它的对称轴,角的对称轴就是角平分线所在的直线。此外,等腰三角形、等腰梯形、长方形(包括正方形)、圆等也都是轴对称图形。其中圆的任意一条直径所在的直线,都是它的对称轴,因此圆有无数条对称轴。(如下图)
轴对称与轴对称图形
两个图形,如果把其中一个图形沿着某一条直线对折,能与另一个图形完全重合,我们就说这两个图形成轴对称,又称这两个图形关于该直线对称。这条直线就是对称轴,两个图形中的对应点叫做关于这条直线的对称点。
一个图形,如果沿一条直线对折, 直线两侧的部分能够完全重合, 那么这个图形就叫做轴对称图形。这条直线就是它的对称轴。(具体如下)
轴对称图形 轴对称
图形
区别 (1)轴对称图形是指一个具有特殊形状的图形,只对一个图形而言。 (2)对称轴不一定只有一条。 (1)轴对称是指两个图形的位置关系,必须涉及两个图形。 (2)只有一条对称轴。
联系 如果把轴对称图形沿对称轴分成两部分,那么这两部分就关于这条直线成轴对称。 如果把两个成轴对称的图形拼在一起看成一个整体,那么它就是一个轴对称图形。
