3.2 数据与结构 第二课时课件(17PPT)-2021-2022学年高中信息技术教科版(2019)必修1
文档属性
| 名称 | 3.2 数据与结构 第二课时课件(17PPT)-2021-2022学年高中信息技术教科版(2019)必修1 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2022-06-19 19:01:59 | ||
图片预览





文档简介
(共17张PPT)
数据与结构
第二课时
第 3 单元
3.2
学习目标
★了解树、图结构的基本概念及其特点。
★根据数据结构的特点,会选用合适的数据结构组织数据解决简单的问题。
【教学重点】数据结构中的树结构和图结构。
【教学难点】数据结构中的树结构和图结构。
数据结构是存在特定关系的数据元素的集合。在解决有些问题时,些相关联的数据将集中在一起,形成一个数据的集合,这种集合能够单独或作为一个整休被访问和处理。
线性数据结构又称为线性表。在线性数据结构中,除首元素没有前趋元素、尾元素没有后继元素外,其他元素都只有个后继元素。
数据结构
线性数据结构
队列
队列是一种有限制的线性结构,它的数据元素只能在一端一次添加(进队),在另一端依次删除(出队)。
A
B
C
D
E
H
G
F
alphabat = [A,B,C,D,E,F,G,H]
我们可以通过对应的方法对列表进行操作:
pop(0)方法可以删除列表的首元素,append方法可以在列表尾部添加一个数据;
例如:
结尾添加字母“I”:alphabat.append(“I”);删除首字母“A”:alphabat.pop(0)
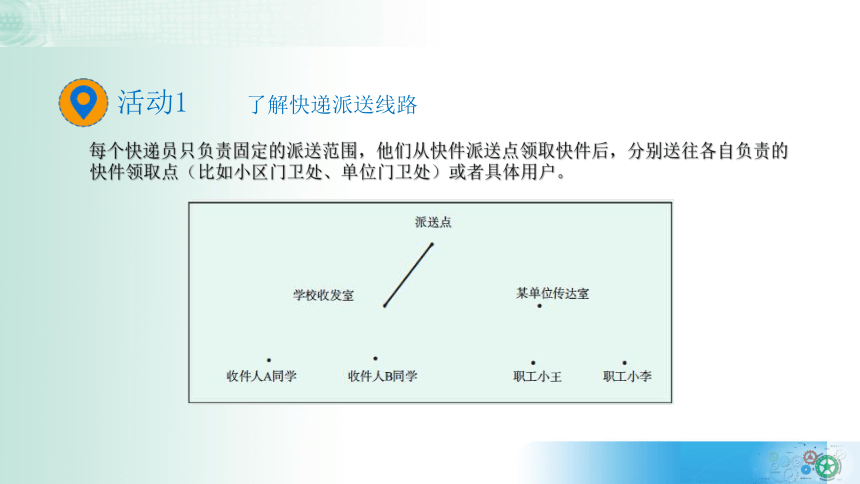
活动1 了解快递派送线路
每个快递员只负责固定的派送范围,他们从快件派送点领取快件后,分别送往各自负责的快件领取点(比如小区门卫处、单位门卫处)或者具体用户。
树结构
树结构是一种具有层次关系的非线性结构。
树是由n(n≥0)个节点组成的有限集合。若n = 0, 则称为空树。任何一个非空树均满足以下两个条件:
(1)仅有一个称为根的节点;
(2)当n>0时,其余节点可分为m(m≥0)个互不相交的有限集合,其中每个集合又是一棵树, 并称为根的子树。
1.A是B,C,D的根节点,B,C,D是A的子树;
2.B是E,F,G的根节点,E,F,G是B的子树;
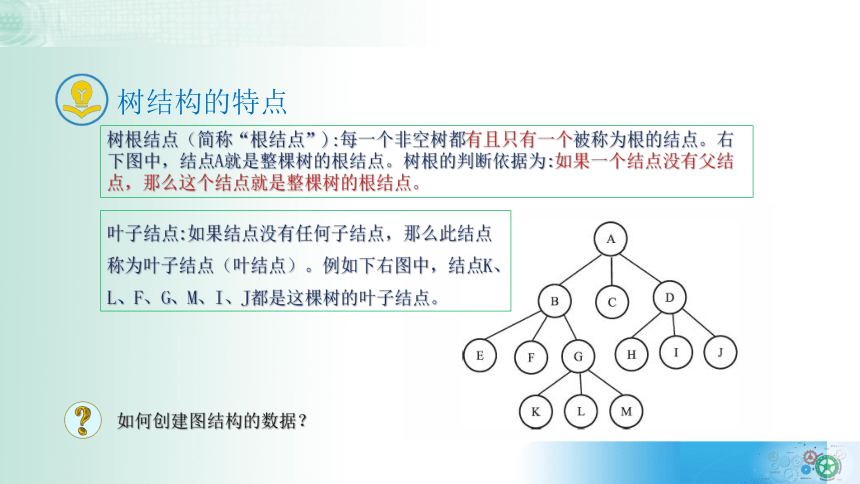
树结构的特点
树根结点(简称“根结点”):每一个非空树都有且只有一个被称为根的结点。右下图中,结点A就是整棵树的根结点。树根的判断依据为:如果一个结点没有父结点,那么这个结点就是整棵树的根结点。
如何创建图结构的数据?
叶子结点:如果结点没有任何子结点,那么此结点称为叶子结点(叶结点)。例如下右图中,结点K、L、F、G、M、I、J都是这棵树的叶子结点。
练一练
创建图结构的数据:
A
B
D
C
E
K
G
F
H
I
J
L
M
list=[“A”] ……………………………………………
list=[(“B”,“C”,“D”)] …………
list=[(“E”.“F”),(“G”),(“H”,“I”,“J”)]
打印字母“G”怎么办?
Print(list[1][0])
活动1 了解物流网络
由于需要综合考虑运营成本,商品在城市间运输的路线是需要计算和规划的。 请你查看图3.2.5中的物流过程,尝试用圆圈表示城市,用线段表示城市之间的送达关系,将图3.2.6补充完整,了解商品配送 的路线特点。
长沙
南京
泰州
图结构
图结构是由一组节点(称为顶点)和一组节点间的连线(称为边或弧)构成的一种数据结构。图结构中的每个顶点都可以与其他顶点有边相连, 图结构中数据元素之间是多对多的关系。
标为“ 1” 的顶点与两条边相连, 顶点“4”与2“,”8“ ,"9"相连。
图结构的应用场景
在物流网络中, 分拨中心、配送中心、货物需求点等可以抽象为图的顶点, 城市道路、各级铁路等可以抽象为图的边, 如城市以及城市之间的运输道路就是图结构。 利用图结构, 我们还可以解决物流中的许多问题, 如道路网络分析、车辆运营安排等。
某同学网购的书已经到达家附近的快递门店,需要他自己去取。不巧的是, 这次购买的三本书是三个不同的物流公司派送的,他家与各快递门店的位置如右图所示。
活动3 规划取快递最快路线
该同学估算了在这些地点之间步行需要的时间, 详见表3.2.2 。
活动3 规划取快递最快路线
请你帮他规划最省时的路线, 然后设计算法解决问题并在下框中描述你的算法。
从起点出发,把当前可以到达的下一个位置列举出来,再从列举出的新位置出发,继续列举下一步可以到达的位置,以此类推,直到返回 起点。
Python中的复合数据类型
我们发现
分析过程的图形是树结构,
树中的节点表示当前所在的位置, 边表示选择的线路。利用树结构,我
们能够更清晰地实现不重复、不遗漏地列举所有做法,更利千通过比较
得到最优解。
请分析队列、树、 图三种结构的区别, 并将结果填在表中
结构类型 数据(节点)之间的关系 生活中相应结构应用举例
队列(线性) 一对一 排队
树 一对多 行政区划、书的目录结构
图 多对多 全国航运图、铁路运输等
课堂小结
数据与结构
数据结构
数据结构举例
集合结构
线性结构(队列)
线性结构:排队
树结构:行政区划
图结构:交通运输
树结构
图结构
数据与结构
第二课时
第 3 单元
3.2
学习目标
★了解树、图结构的基本概念及其特点。
★根据数据结构的特点,会选用合适的数据结构组织数据解决简单的问题。
【教学重点】数据结构中的树结构和图结构。
【教学难点】数据结构中的树结构和图结构。
数据结构是存在特定关系的数据元素的集合。在解决有些问题时,些相关联的数据将集中在一起,形成一个数据的集合,这种集合能够单独或作为一个整休被访问和处理。
线性数据结构又称为线性表。在线性数据结构中,除首元素没有前趋元素、尾元素没有后继元素外,其他元素都只有个后继元素。
数据结构
线性数据结构
队列
队列是一种有限制的线性结构,它的数据元素只能在一端一次添加(进队),在另一端依次删除(出队)。
A
B
C
D
E
H
G
F
alphabat = [A,B,C,D,E,F,G,H]
我们可以通过对应的方法对列表进行操作:
pop(0)方法可以删除列表的首元素,append方法可以在列表尾部添加一个数据;
例如:
结尾添加字母“I”:alphabat.append(“I”);删除首字母“A”:alphabat.pop(0)
活动1 了解快递派送线路
每个快递员只负责固定的派送范围,他们从快件派送点领取快件后,分别送往各自负责的快件领取点(比如小区门卫处、单位门卫处)或者具体用户。
树结构
树结构是一种具有层次关系的非线性结构。
树是由n(n≥0)个节点组成的有限集合。若n = 0, 则称为空树。任何一个非空树均满足以下两个条件:
(1)仅有一个称为根的节点;
(2)当n>0时,其余节点可分为m(m≥0)个互不相交的有限集合,其中每个集合又是一棵树, 并称为根的子树。
1.A是B,C,D的根节点,B,C,D是A的子树;
2.B是E,F,G的根节点,E,F,G是B的子树;
树结构的特点
树根结点(简称“根结点”):每一个非空树都有且只有一个被称为根的结点。右下图中,结点A就是整棵树的根结点。树根的判断依据为:如果一个结点没有父结点,那么这个结点就是整棵树的根结点。
如何创建图结构的数据?
叶子结点:如果结点没有任何子结点,那么此结点称为叶子结点(叶结点)。例如下右图中,结点K、L、F、G、M、I、J都是这棵树的叶子结点。
练一练
创建图结构的数据:
A
B
D
C
E
K
G
F
H
I
J
L
M
list=[“A”] ……………………………………………
list=[(“B”,“C”,“D”)] …………
list=[(“E”.“F”),(“G”),(“H”,“I”,“J”)]
打印字母“G”怎么办?
Print(list[1][0])
活动1 了解物流网络
由于需要综合考虑运营成本,商品在城市间运输的路线是需要计算和规划的。 请你查看图3.2.5中的物流过程,尝试用圆圈表示城市,用线段表示城市之间的送达关系,将图3.2.6补充完整,了解商品配送 的路线特点。
长沙
南京
泰州
图结构
图结构是由一组节点(称为顶点)和一组节点间的连线(称为边或弧)构成的一种数据结构。图结构中的每个顶点都可以与其他顶点有边相连, 图结构中数据元素之间是多对多的关系。
标为“ 1” 的顶点与两条边相连, 顶点“4”与2“,”8“ ,"9"相连。
图结构的应用场景
在物流网络中, 分拨中心、配送中心、货物需求点等可以抽象为图的顶点, 城市道路、各级铁路等可以抽象为图的边, 如城市以及城市之间的运输道路就是图结构。 利用图结构, 我们还可以解决物流中的许多问题, 如道路网络分析、车辆运营安排等。
某同学网购的书已经到达家附近的快递门店,需要他自己去取。不巧的是, 这次购买的三本书是三个不同的物流公司派送的,他家与各快递门店的位置如右图所示。
活动3 规划取快递最快路线
该同学估算了在这些地点之间步行需要的时间, 详见表3.2.2 。
活动3 规划取快递最快路线
请你帮他规划最省时的路线, 然后设计算法解决问题并在下框中描述你的算法。
从起点出发,把当前可以到达的下一个位置列举出来,再从列举出的新位置出发,继续列举下一步可以到达的位置,以此类推,直到返回 起点。
Python中的复合数据类型
我们发现
分析过程的图形是树结构,
树中的节点表示当前所在的位置, 边表示选择的线路。利用树结构,我
们能够更清晰地实现不重复、不遗漏地列举所有做法,更利千通过比较
得到最优解。
请分析队列、树、 图三种结构的区别, 并将结果填在表中
结构类型 数据(节点)之间的关系 生活中相应结构应用举例
队列(线性) 一对一 排队
树 一对多 行政区划、书的目录结构
图 多对多 全国航运图、铁路运输等
课堂小结
数据与结构
数据结构
数据结构举例
集合结构
线性结构(队列)
线性结构:排队
树结构:行政区划
图结构:交通运输
树结构
图结构
