华东师大版数学八年级下册教案:第20章数据的整理与初步处理20.3数据的离散程度
文档属性
| 名称 | 华东师大版数学八年级下册教案:第20章数据的整理与初步处理20.3数据的离散程度 |

|
|
| 格式 | docx | ||
| 文件大小 | 794.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 21:17:04 | ||
图片预览


文档简介
第20章 数据的整理与初步处理
20.3 数据的离散程度
教学目标 1.理解极差、方差与标准差的概念与作用. 2.灵活运用方差与标准差来处理数据. 3.能用计算器求数据的方差和标准差. 教学重难点 重点:对方差和标准差概念的理解. 难点:应用方差和标准差分析数据,并做出决策. 教学过程 新课导入 小明七年级时对数学不感兴趣,遇到问题不爱动脑筋,因此他的数学成绩不太好,七年级的一学年中四次考试的数学成绩分别是分,分,分,分.七年级暑假时,小明参加了科技活动小组,在活动中,小明体会到学好数学的重要性,逐渐对数学产生了兴趣,因此小明的数学成绩进步很快.八年级的一学年中,小明在四次考试中的数学成绩分别是分,分,分,分. 看完这则小通讯,请你谈谈你的看法.你认为在这些数据中最能反映学习兴趣重要性的是哪一对数据?两者相差多少? 分析:最能反映学习兴趣重要性的是七年级时的分和八年级时的分,两者相差达分. 【设计】教师提问,学生回答,教师根据学生的答案进行引导,引出本节课的课题. 合作探究 1.最大值与最小值的差(极差) 下表显示的是上海市年月下旬和年同期的每日最高气温,如何对这两段时间的气温进行比较呢 上海市每日最高气温统计表(单位:℃) 2月 21日2月 22日2月 23日2月 24日2月 25日2月 26日2月 27日2月 28日2001年12131422689122002年131312911161210
(1)试对这两段时间的气温进行比较. 由表中的数据可知,年月下旬和年同期的气温相比,有天的温度相对高些,有天的温度相对低些,还有天的温度相同. (2)我们可以由此认为年月下旬的气温总体上比年同期高吗? 经计算可以看出,对于月下旬的这段时间而言,年和年上海地区的平均气温相等,都是℃. (3)这是不是说,两个时段的气温情况总体上没有什么差异呢?请同学们根据上表提供的数据,绘制出相应的折线图.下面是根据两段时间的气温情况绘成的折线图. (4)观察一下,你感觉它们有没有差异呢?把你通过观察得到的判断写在下面的横线上:_____________________________________________________. 通过观察,我们可以发现:图(a)中折线波动的范围比较大——从℃到℃,图(b)中折线波动的范围则比较小——从℃到℃. 【讨论交流】什么样的指标可以反映一组数据变化范围的大小? 【总结】我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.它反映一组数据的两个极端值之间的差异情况,对其他数据的波动情况不敏感. 例如在上图中我们可以看出,图(a)中最高气温与最低气温之间差距很大,相差℃;图(b)中最高气温与最低气温之间的差距为℃,所以从图中看,总体上气温变化的范围不太大. 2.方差 【交流发现】(1)我们来看这样一个问题:小明和小兵参加体育项目训练,近期的次测试成绩如表1: 表1 测试次数12345小明1314131213小兵1013161412
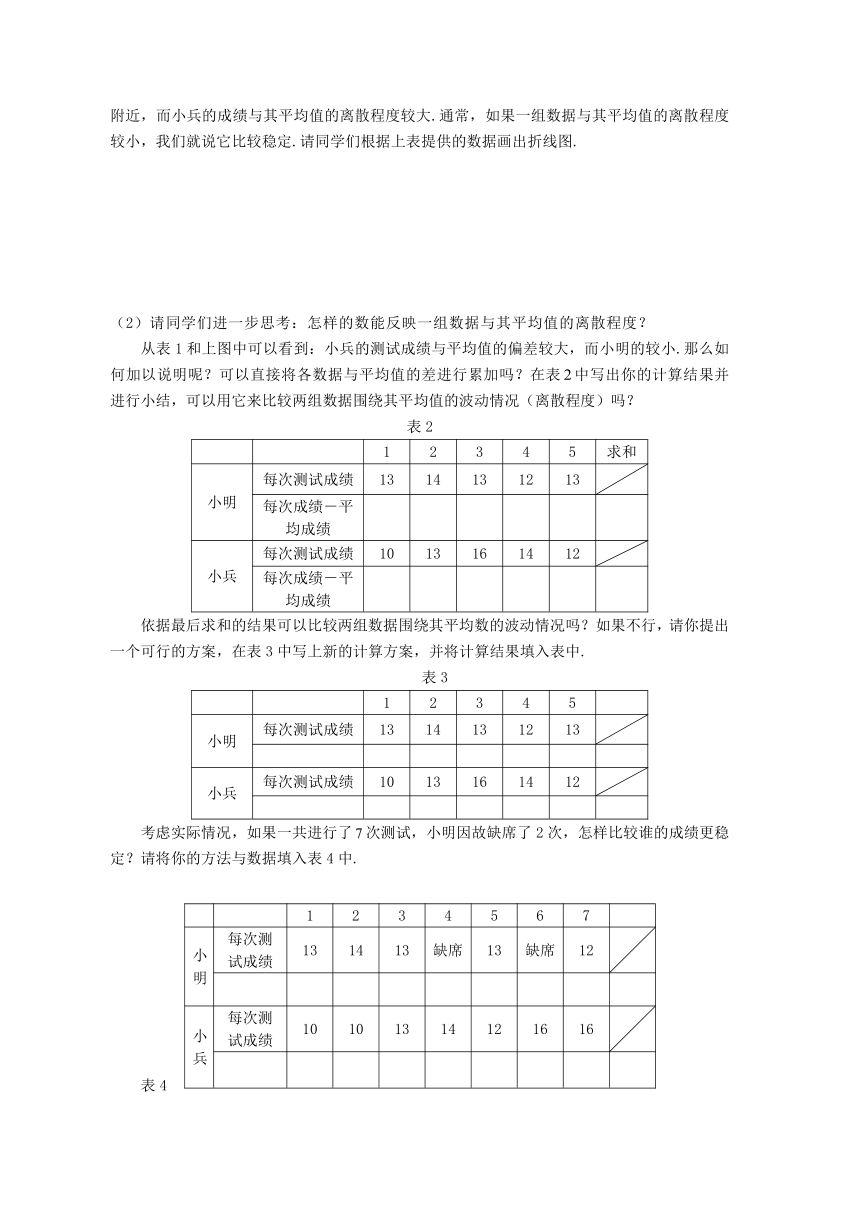
谁的成绩较为稳定?为什么? 由计算可知,两人测试成绩的平均值都是分,但相比之下,小明的成绩大都集中在分附近,而小兵的成绩与其平均值的离散程度较大.通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.请同学们根据上表提供的数据画出折线图. (2)请同学们进一步思考:怎样的数能反映一组数据与其平均值的离散程度? 从表1和上图中可以看到:小兵的测试成绩与平均值的偏差较大,而小明的较小.那么如何加以说明呢?可以直接将各数据与平均值的差进行累加吗?在表中写出你的计算结果并进行小结,可以用它来比较两组数据围绕其平均值的波动情况(离散程度)吗? 表2 12345求和小明每次测试成绩1314131213每次成绩-平均成绩小兵每次测试成绩1013161412每次成绩-平均成绩
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?如果不行,请你提出一个可行的方案,在表3中写上新的计算方案,并将计算结果填入表中. 表3 12345小明每次测试成绩1314131213小兵每次测试成绩1013161412
考虑实际情况,如果一共进行了次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表4中. 1234567小明每次测试成绩131413缺席13缺席12小兵每次测试成绩10101314121616
表4 通过两张表格的对比让学生进一步明白:为什么要用“每次成绩”和“平均成绩”相减?为什么要“平方”?为什么求“平均数”比“求和”好? 【归纳总结】我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差(variance). 我们通常用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是. 【注意】(1)方差是用来描述一组数据中每一个数据与这组数据的平均数的偏离程度的量.一组数据的方差越大,说明数据的波动越大,同时离散程度也越大. (2)方差的计算方法是 “先平均,再求差,然后平方,最后再平均.” 例题讲解 例1 求数据7,6,8,8,5,9,7,7,6,7的方差. 【问题探索】怎样求一组数据的方差? 解法一:因为这组数据的平均数为 , 所以 . 解法二:将各数据减7,得新数据:0,-1,1,1,-2,2,0,0,-1,0. 由题易知,新数据的平均数为0, 所以. 例2 对盆同一种的花施肥,用甲、乙两种保花肥,把盆花分成两组,每组盆,对其花期记录如下:(单位:天) 甲组2523282227乙组2724242723
(1)盆花的花期最多相差几天? (2)施用哪种保花肥,使得花的平均花期较长? (3)施用哪种保花肥效果比较可靠? 分析:花的平均花期就是分别求出甲、乙两组数据的平均数,而看哪种保花肥效果可靠,就是比较它们的方差. 解:(1)(天). (2)由平均数计算公式可得: (天); (天) 因为,所以无论施用哪种花肥,花的平均花期一样长. (3)由方差计算公式,得,.因为,所以施用乙种保花肥比较可靠. 3.用计算器求方差 下面以计算年月下旬上海最高气温的方差为例. 年月下旬上海每日最高气温统计表 日期2122232425262728温度/℃131312911161210
按键顺序如下: (1) ,打开计算器; (2),启动“单变量统计”计算功能; (3) ,输入所有数据; (4) ,即可获得这组数据的统计值,其中方差=4. 例题讲解 例3 用科学计算器求下列数据的方差: 271,315,263,289,300,277,286,293,297,280. 【思考】用科学计算器求方差的步骤是什么? 解:(1),打开计算器; (2),启动“单变量统计”计算功能; (3)输入所有数据; (4),计算出数据的方差σ2x=207.49. 【总结】(学生总结,老师点评)熟悉用科学计算器求方差的方法和步骤是关键. 课堂练习 1.人数相同的八年级(1)(2)两班学生在同一次数学单元测试成绩中班级平均分和方差如下:,,成绩较为稳定的班级是( ) A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定 2.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是( ) A.4,15 B.3,15 C.4,16 D.3,16 3.将一组数据中的每个数据都减去同一个数,那么下列结论成立的是( ) A.方差改变,平均数不变 B.方差和平均数都不变 C.方差改变,平均数改变 D.方差不变,平均数改变 4.(1)已知一组数据1,2,3,4,5的方差为2,则另一组数据11,12,13,14,15的方差为 . (2)已知一组数据的方差是,则新的一组数据 (a为常数,a≠0)的方差为 .(用含a,s的代数式表示) 参考答案 1.B 2.A 3. D 4.(1)2 (2) 课堂小结 用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是 【注意】(1)方差是用来描述一组数据中每一个数据与这组数据的平均数的偏离程度的量.一组数据的方差越大,说明数据的波动越大,同时离散程度也越大. (2)方差的计算方法是 “先平均,再求差,然后平方,最后再平均.” 布置作业 教材P155习题 板书设计 20.3 数据的离散程度 1. 方差的概念 用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是 2.利用方差的大小判断数据稳定性的步骤 (1)计算数据的平均数; (2)计算方差; (3)根据方差大小作出判断. 例题
20.3 数据的离散程度
教学目标 1.理解极差、方差与标准差的概念与作用. 2.灵活运用方差与标准差来处理数据. 3.能用计算器求数据的方差和标准差. 教学重难点 重点:对方差和标准差概念的理解. 难点:应用方差和标准差分析数据,并做出决策. 教学过程 新课导入 小明七年级时对数学不感兴趣,遇到问题不爱动脑筋,因此他的数学成绩不太好,七年级的一学年中四次考试的数学成绩分别是分,分,分,分.七年级暑假时,小明参加了科技活动小组,在活动中,小明体会到学好数学的重要性,逐渐对数学产生了兴趣,因此小明的数学成绩进步很快.八年级的一学年中,小明在四次考试中的数学成绩分别是分,分,分,分. 看完这则小通讯,请你谈谈你的看法.你认为在这些数据中最能反映学习兴趣重要性的是哪一对数据?两者相差多少? 分析:最能反映学习兴趣重要性的是七年级时的分和八年级时的分,两者相差达分. 【设计】教师提问,学生回答,教师根据学生的答案进行引导,引出本节课的课题. 合作探究 1.最大值与最小值的差(极差) 下表显示的是上海市年月下旬和年同期的每日最高气温,如何对这两段时间的气温进行比较呢 上海市每日最高气温统计表(单位:℃) 2月 21日2月 22日2月 23日2月 24日2月 25日2月 26日2月 27日2月 28日2001年12131422689122002年131312911161210
(1)试对这两段时间的气温进行比较. 由表中的数据可知,年月下旬和年同期的气温相比,有天的温度相对高些,有天的温度相对低些,还有天的温度相同. (2)我们可以由此认为年月下旬的气温总体上比年同期高吗? 经计算可以看出,对于月下旬的这段时间而言,年和年上海地区的平均气温相等,都是℃. (3)这是不是说,两个时段的气温情况总体上没有什么差异呢?请同学们根据上表提供的数据,绘制出相应的折线图.下面是根据两段时间的气温情况绘成的折线图. (4)观察一下,你感觉它们有没有差异呢?把你通过观察得到的判断写在下面的横线上:_____________________________________________________. 通过观察,我们可以发现:图(a)中折线波动的范围比较大——从℃到℃,图(b)中折线波动的范围则比较小——从℃到℃. 【讨论交流】什么样的指标可以反映一组数据变化范围的大小? 【总结】我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.它反映一组数据的两个极端值之间的差异情况,对其他数据的波动情况不敏感. 例如在上图中我们可以看出,图(a)中最高气温与最低气温之间差距很大,相差℃;图(b)中最高气温与最低气温之间的差距为℃,所以从图中看,总体上气温变化的范围不太大. 2.方差 【交流发现】(1)我们来看这样一个问题:小明和小兵参加体育项目训练,近期的次测试成绩如表1: 表1 测试次数12345小明1314131213小兵1013161412
谁的成绩较为稳定?为什么? 由计算可知,两人测试成绩的平均值都是分,但相比之下,小明的成绩大都集中在分附近,而小兵的成绩与其平均值的离散程度较大.通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.请同学们根据上表提供的数据画出折线图. (2)请同学们进一步思考:怎样的数能反映一组数据与其平均值的离散程度? 从表1和上图中可以看到:小兵的测试成绩与平均值的偏差较大,而小明的较小.那么如何加以说明呢?可以直接将各数据与平均值的差进行累加吗?在表中写出你的计算结果并进行小结,可以用它来比较两组数据围绕其平均值的波动情况(离散程度)吗? 表2 12345求和小明每次测试成绩1314131213每次成绩-平均成绩小兵每次测试成绩1013161412每次成绩-平均成绩
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?如果不行,请你提出一个可行的方案,在表3中写上新的计算方案,并将计算结果填入表中. 表3 12345小明每次测试成绩1314131213小兵每次测试成绩1013161412
考虑实际情况,如果一共进行了次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表4中. 1234567小明每次测试成绩131413缺席13缺席12小兵每次测试成绩10101314121616
表4 通过两张表格的对比让学生进一步明白:为什么要用“每次成绩”和“平均成绩”相减?为什么要“平方”?为什么求“平均数”比“求和”好? 【归纳总结】我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差(variance). 我们通常用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是. 【注意】(1)方差是用来描述一组数据中每一个数据与这组数据的平均数的偏离程度的量.一组数据的方差越大,说明数据的波动越大,同时离散程度也越大. (2)方差的计算方法是 “先平均,再求差,然后平方,最后再平均.” 例题讲解 例1 求数据7,6,8,8,5,9,7,7,6,7的方差. 【问题探索】怎样求一组数据的方差? 解法一:因为这组数据的平均数为 , 所以 . 解法二:将各数据减7,得新数据:0,-1,1,1,-2,2,0,0,-1,0. 由题易知,新数据的平均数为0, 所以. 例2 对盆同一种的花施肥,用甲、乙两种保花肥,把盆花分成两组,每组盆,对其花期记录如下:(单位:天) 甲组2523282227乙组2724242723
(1)盆花的花期最多相差几天? (2)施用哪种保花肥,使得花的平均花期较长? (3)施用哪种保花肥效果比较可靠? 分析:花的平均花期就是分别求出甲、乙两组数据的平均数,而看哪种保花肥效果可靠,就是比较它们的方差. 解:(1)(天). (2)由平均数计算公式可得: (天); (天) 因为,所以无论施用哪种花肥,花的平均花期一样长. (3)由方差计算公式,得,.因为,所以施用乙种保花肥比较可靠. 3.用计算器求方差 下面以计算年月下旬上海最高气温的方差为例. 年月下旬上海每日最高气温统计表 日期2122232425262728温度/℃131312911161210
按键顺序如下: (1) ,打开计算器; (2),启动“单变量统计”计算功能; (3) ,输入所有数据; (4) ,即可获得这组数据的统计值,其中方差=4. 例题讲解 例3 用科学计算器求下列数据的方差: 271,315,263,289,300,277,286,293,297,280. 【思考】用科学计算器求方差的步骤是什么? 解:(1),打开计算器; (2),启动“单变量统计”计算功能; (3)输入所有数据; (4),计算出数据的方差σ2x=207.49. 【总结】(学生总结,老师点评)熟悉用科学计算器求方差的方法和步骤是关键. 课堂练习 1.人数相同的八年级(1)(2)两班学生在同一次数学单元测试成绩中班级平均分和方差如下:,,成绩较为稳定的班级是( ) A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定 2.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是( ) A.4,15 B.3,15 C.4,16 D.3,16 3.将一组数据中的每个数据都减去同一个数,那么下列结论成立的是( ) A.方差改变,平均数不变 B.方差和平均数都不变 C.方差改变,平均数改变 D.方差不变,平均数改变 4.(1)已知一组数据1,2,3,4,5的方差为2,则另一组数据11,12,13,14,15的方差为 . (2)已知一组数据的方差是,则新的一组数据 (a为常数,a≠0)的方差为 .(用含a,s的代数式表示) 参考答案 1.B 2.A 3. D 4.(1)2 (2) 课堂小结 用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是 【注意】(1)方差是用来描述一组数据中每一个数据与这组数据的平均数的偏离程度的量.一组数据的方差越大,说明数据的波动越大,同时离散程度也越大. (2)方差的计算方法是 “先平均,再求差,然后平方,最后再平均.” 布置作业 教材P155习题 板书设计 20.3 数据的离散程度 1. 方差的概念 用表示一组数据的方差,用表示一组数据的平均数,,,…,表示各原始数据.那么这个数据的方差公式是 2.利用方差的大小判断数据稳定性的步骤 (1)计算数据的平均数; (2)计算方差; (3)根据方差大小作出判断. 例题
