6.3 三角形的中位线 课件(共27张PPT)
文档属性
| 名称 | 6.3 三角形的中位线 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 21:28:51 | ||
图片预览



文档简介
(共27张PPT)
6.3 三角形的中位线
第六章
平行四边形
八年级数学下册同步(北师大版)
1.理解三角形中位线的概念;
2.经历探索三角形中位线定理的过程,会证明三角形的中位线定理;
3.能应用三角形中位线定理解决简单问题;
4.体会转化思想,培养几何直观、推理能力.
学习目标
导入新课
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
导入新课
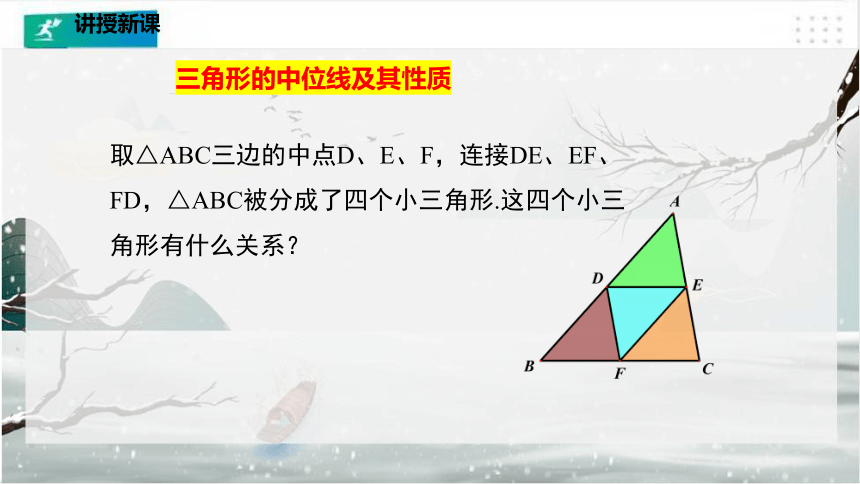
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC,你知道为什么吗?
A
B
C
D
E
讲授新课
三角形的中位线及其性质
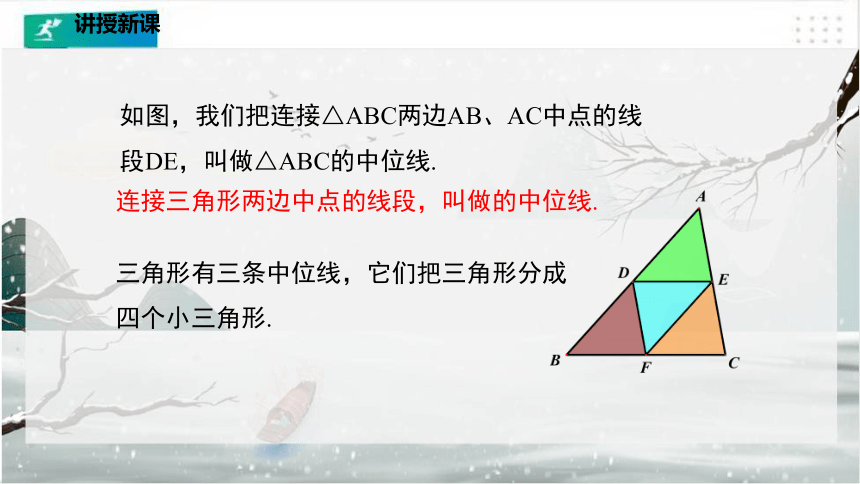
取△ABC三边的中点D、E、F,连接DE、EF、FD,△ABC被分成了四个小三角形.这四个小三角形有什么关系?
讲授新课
三角形有三条中位线,它们把三角形分成四个小三角形.
连接三角形两边中点的线段,叫做的中位线.
如图,我们把连接△ABC两边AB、AC中点的线段DE,叫做△ABC的中位线.
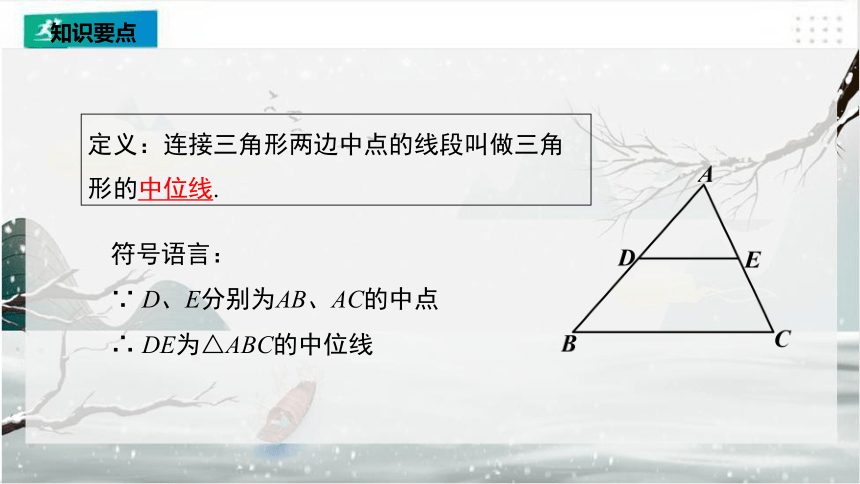
定义:连接三角形两边中点的线段叫做三角形的中位线.
符号语言:
∵ D、E分别为AB、AC的中点
∴ DE为△ABC的中位线
知识要点
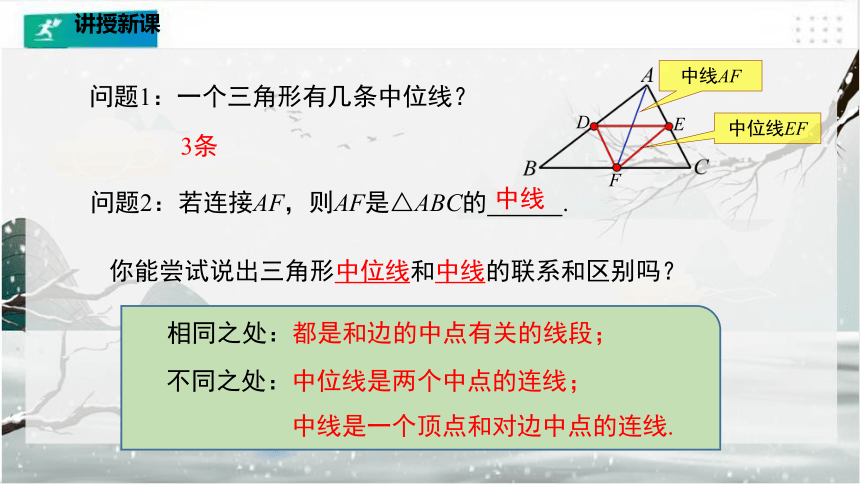
不同之处:中位线是两个中点的连线;
中线是一个顶点和对边中点的连线.
相同之处:都是和边的中点有关的线段;
讲授新课
问题1:一个三角形有几条中位线?
D
E
F
3条
问题2:若连接AF,则AF是△ABC的 .
中线AF
中位线EF
你能尝试说出三角形中位线和中线的联系和区别吗?
中线
讲授新课
B
A
C
D
E
F
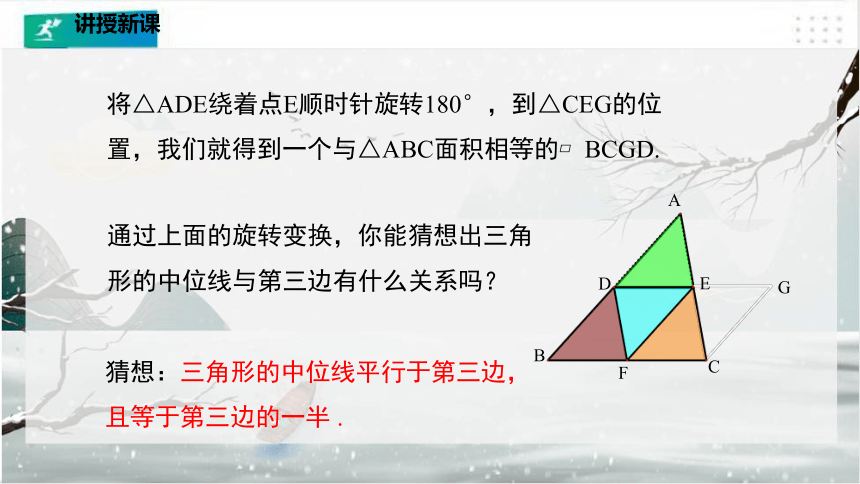
将△ADE绕着点E顺时针旋转180°,到△CEG的位置,我们就得到一个与△ABC面积相等的 BCGD.
G
通过上面的旋转变换,你能猜想出三角形的中位线与第三边有什么关系吗?
猜想:三角形的中位线平行于第三边,且等于第三边的一半 .
讲授新课
已知:在△ABC中,DE是△ABC的中位线.
求证:DE∥BC,DE= BC
E
A
B
C
D
如何将两个问题转化为一个问题呢?作辅助线:倍长DE
讲授新课
如图,延长DE到F,使FE=DE,连接CF.
在△ADE和△CFE中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE≌△CFE.
∴∠A=∠ECF,AD=CF.∴CF∥AB.
∵BD=AD,∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等
的四边形是平行四边形).
∴ DF∥BC(平行四边形的定义),
DF=BC(平行四边形的对边相等).
∴DE∥BC,DE= BC
E
A
B
C
D
F
2
1
三角形的中位线平行于第三边,并且等于第三边的一半.
∵ DE是△ABC的中位线
∴ DE∥BC,DE= BC
(位置关系)(数量关系)
符号语言:
作用:1、证明两条线段平行;
2、证明一条线段是另一条线段的2倍或 .
知识要点
讲授新课
中点四边形
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
∴EF∥AC,,
HG∥AC,.
顺次连接四边形各边中点的线段组成一个平行四边形.
讲授新课
(1) 顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
(3)顺次连结正方形各边中点所得的四边形是什么?
平行四边形
矩形
正方形
试一试
讲授新课
试一试
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
讲授新课
试一试
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
知识要点
当堂检测
1. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3, E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
A.12 B.14 C.24 D.21
A
当堂检测
2. 如图,已知长方形ABCD中,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长先增大后减小
C
当堂检测
3、如图2,D,E,F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
A.5 B.10 C.20 D.40
C
当堂检测
4. 如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m B.48 m
C.45 m D.35 m
B
当堂检测
5.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点:
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
当堂检测
6. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
当堂检测
7.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂小结
三角形的中位线
定 义
连结三角形两边中点的线段叫做三角形的中位线.
性质
三角形的中位线平行于第三边,且等于第三边的一半.
应用
①周长;
②面积;
③综合应用.
https://www.21cnjy.com/help/help_extract.php
6.3 三角形的中位线
第六章
平行四边形
八年级数学下册同步(北师大版)
1.理解三角形中位线的概念;
2.经历探索三角形中位线定理的过程,会证明三角形的中位线定理;
3.能应用三角形中位线定理解决简单问题;
4.体会转化思想,培养几何直观、推理能力.
学习目标
导入新课
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
导入新课
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC,你知道为什么吗?
A
B
C
D
E
讲授新课
三角形的中位线及其性质
取△ABC三边的中点D、E、F,连接DE、EF、FD,△ABC被分成了四个小三角形.这四个小三角形有什么关系?
讲授新课
三角形有三条中位线,它们把三角形分成四个小三角形.
连接三角形两边中点的线段,叫做的中位线.
如图,我们把连接△ABC两边AB、AC中点的线段DE,叫做△ABC的中位线.
定义:连接三角形两边中点的线段叫做三角形的中位线.
符号语言:
∵ D、E分别为AB、AC的中点
∴ DE为△ABC的中位线
知识要点
不同之处:中位线是两个中点的连线;
中线是一个顶点和对边中点的连线.
相同之处:都是和边的中点有关的线段;
讲授新课
问题1:一个三角形有几条中位线?
D
E
F
3条
问题2:若连接AF,则AF是△ABC的 .
中线AF
中位线EF
你能尝试说出三角形中位线和中线的联系和区别吗?
中线
讲授新课
B
A
C
D
E
F
将△ADE绕着点E顺时针旋转180°,到△CEG的位置,我们就得到一个与△ABC面积相等的 BCGD.
G
通过上面的旋转变换,你能猜想出三角形的中位线与第三边有什么关系吗?
猜想:三角形的中位线平行于第三边,且等于第三边的一半 .
讲授新课
已知:在△ABC中,DE是△ABC的中位线.
求证:DE∥BC,DE= BC
E
A
B
C
D
如何将两个问题转化为一个问题呢?作辅助线:倍长DE
讲授新课
如图,延长DE到F,使FE=DE,连接CF.
在△ADE和△CFE中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE≌△CFE.
∴∠A=∠ECF,AD=CF.∴CF∥AB.
∵BD=AD,∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等
的四边形是平行四边形).
∴ DF∥BC(平行四边形的定义),
DF=BC(平行四边形的对边相等).
∴DE∥BC,DE= BC
E
A
B
C
D
F
2
1
三角形的中位线平行于第三边,并且等于第三边的一半.
∵ DE是△ABC的中位线
∴ DE∥BC,DE= BC
(位置关系)(数量关系)
符号语言:
作用:1、证明两条线段平行;
2、证明一条线段是另一条线段的2倍或 .
知识要点
讲授新课
中点四边形
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
∴EF∥AC,,
HG∥AC,.
顺次连接四边形各边中点的线段组成一个平行四边形.
讲授新课
(1) 顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
(3)顺次连结正方形各边中点所得的四边形是什么?
平行四边形
矩形
正方形
试一试
讲授新课
试一试
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
讲授新课
试一试
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
知识要点
当堂检测
1. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3, E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
A.12 B.14 C.24 D.21
A
当堂检测
2. 如图,已知长方形ABCD中,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长先增大后减小
C
当堂检测
3、如图2,D,E,F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
A.5 B.10 C.20 D.40
C
当堂检测
4. 如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m B.48 m
C.45 m D.35 m
B
当堂检测
5.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点:
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
当堂检测
6. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
当堂检测
7.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂小结
三角形的中位线
定 义
连结三角形两边中点的线段叫做三角形的中位线.
性质
三角形的中位线平行于第三边,且等于第三边的一半.
应用
①周长;
②面积;
③综合应用.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
