三角函数的图像与性质
图片预览






文档简介
课件27张PPT。三角函数图像与性质 正弦、余弦函数的图象 三角函数三角函数线正弦函数
余弦函数
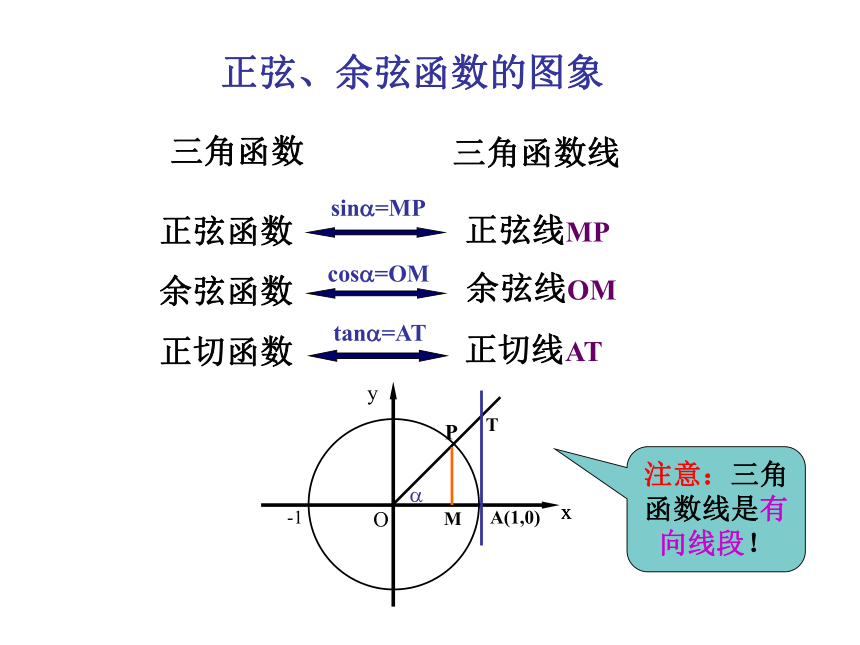
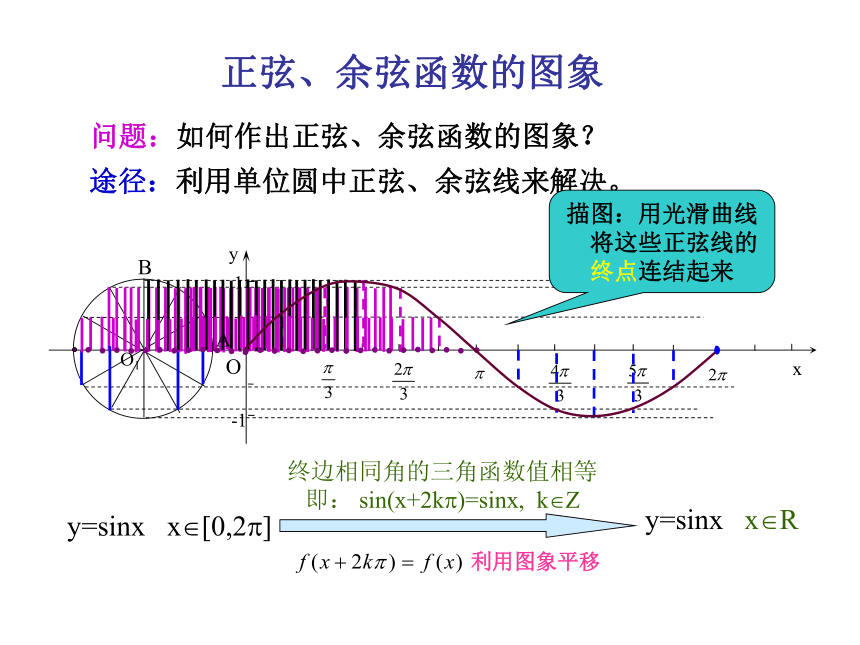
正切函数正切线AT 正弦、余弦函数的图象 ?PMA(1,0)Tsin?=MPcos?=OMtan?=AT注意:三角函数线是有向线段!正弦线MP余弦线OM 正弦、余弦函数的图象 问题:如何作出正弦、余弦函数的图象?途径:利用单位圆中正弦、余弦线来解决。 y=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 描图:用光滑曲线
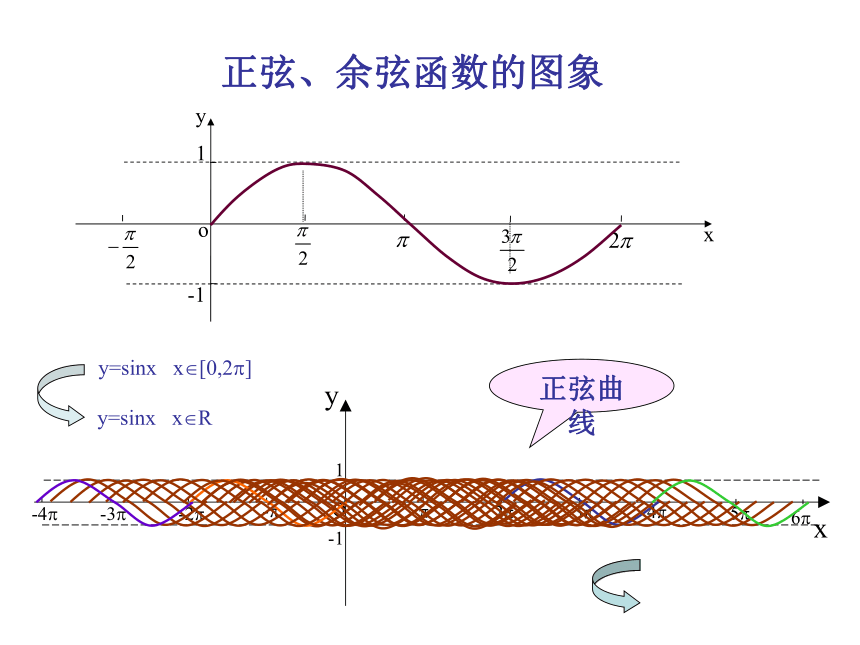
将这些正弦线的终点连结起来利用图象平移AB 正弦、余弦函数的图象 正弦曲线 正弦、余弦函数的图象 如何作出正弦函数的图象(在精确度要求不太高时)?(0,0)( ? ,0)( 2? ,0)五点画图法五点法—— 定义域(1) 值域x?R[ -1, 1 ] 二、正弦函数的性质观察正弦曲线,得出正弦函数的性质:新授周 期 的 概 念 一般地,对于函数 f (x),如果存在一个非零常数 T ,使得当 x 取定义域内的每一个值时,都有 f ( x+T )= f (x),那么函数 f (x) 就叫做周期函数,非零常数 T 叫做这个函数的周期.
对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.新授 由公式 sin (x+k · 2 ?)=sin x (k?Z) 可知:
正弦函数是一个周期函数,2? ,4? ,… ,-2? ,-4? ,… , 2k ?(k?Z 且 k≠0)都是正弦函数的周期.
2 ? 是其最小正周期 . (2) 正弦函数的周期性新授 (3) 正弦函数的奇偶性由公式 sin(-x)=-sin x图象关于原点成中心对称 .正弦函数是奇函数.新授在闭区间 上, 是增函数; (4) 正弦函数的单调性-1 0 1 0 -1在闭区间 上,是减函数.观察正弦函数图象新授1. 诱导公式.
2. 正弦曲线的五点作图法.
3. 填表:10-1010复习一、余弦函数的图象 余弦函数图象的五个关键点:与 x 轴的交点图象的最高点图象的最低点五点
作图法
新授 由诱导公式 cos( x+2k?)=cos x,将 y=cos x ,x?[0,2 ?] 的图象沿 x 轴向左、右平移2 ?, 4 ? ,…,
就可得到 y=cos x的图象.余 弦 曲 线 新授二、余弦函数的性质 定义域 x ? R ,值 域 y?[- 1, 1]. 当 x=2 k?,k ? Z 时,
y=cos x 取得最大值1,即 ymax=1;
当 x= (2 k+1) ? , k ? Z 时,
y=cos x 取得最小值 -1,即 ymin=-1. 观察余弦曲线(1) 余弦函数的值域新授 由公式 cos(x+k · 2? )=cos x ( k ? Z )
可知:
余弦函数是一个周期函数,2? ,4? ,…,-2? ,-4? ,… , 2k? ( k ? Z 且 k≠0 )
都是余弦函数的周期;
2? 是其最小正周期. (2) 余弦函数的周期 余弦函数的图象每隔 2? 重复出现. 新授(3) 余弦函数的奇偶性 由公式 cos(-x)=cos x 余弦函数是偶函数.图象关于 y 轴成轴对称 . 新授(4) 余弦函数的单调性 观察余弦曲线-1 0 1 0 -1在 [(2 k-1) ?, 2 k?] (k?Z)上,是增函数; 在 [2 k?,(2 k+1)? ] (k?Z)上,是减函数. 新授 正弦、余弦函数的图象 例1 画出函数y=1+sinx,x?[0, 2?]的简图:010-10 1 2 1 0 1 o1-12y=sinx,x?[0, 2?]y=1+sinx,x?[0, 2?]步骤:
1.列表
2.描点
3.连线例 2 求使函数 y=2+sin x 取最大值、最小值
的 x 的集合,并求出这个函数的最大值,
最小值和周期 T .解例题讲解 正弦、余弦函数的图象 y=sinx,x?[0, 2?]100-10 正弦、余弦函数的图象 正弦、余弦函数的图象 小
结1. 正弦曲线、余弦曲线2.注意与诱导公式、三角函数线等知识的联系y=sinx,x?[0, 2?]y=cosx,x?[0, 2?] 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 余弦曲线(0,1)( ? ,-1)( 2? ,1)正弦曲线形状完全一样只是位置不同
余弦函数
正切函数正切线AT 正弦、余弦函数的图象 ?PMA(1,0)Tsin?=MPcos?=OMtan?=AT注意:三角函数线是有向线段!正弦线MP余弦线OM 正弦、余弦函数的图象 问题:如何作出正弦、余弦函数的图象?途径:利用单位圆中正弦、余弦线来解决。 y=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 描图:用光滑曲线
将这些正弦线的终点连结起来利用图象平移AB 正弦、余弦函数的图象 正弦曲线 正弦、余弦函数的图象 如何作出正弦函数的图象(在精确度要求不太高时)?(0,0)( ? ,0)( 2? ,0)五点画图法五点法—— 定义域(1) 值域x?R[ -1, 1 ] 二、正弦函数的性质观察正弦曲线,得出正弦函数的性质:新授周 期 的 概 念 一般地,对于函数 f (x),如果存在一个非零常数 T ,使得当 x 取定义域内的每一个值时,都有 f ( x+T )= f (x),那么函数 f (x) 就叫做周期函数,非零常数 T 叫做这个函数的周期.
对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.新授 由公式 sin (x+k · 2 ?)=sin x (k?Z) 可知:
正弦函数是一个周期函数,2? ,4? ,… ,-2? ,-4? ,… , 2k ?(k?Z 且 k≠0)都是正弦函数的周期.
2 ? 是其最小正周期 . (2) 正弦函数的周期性新授 (3) 正弦函数的奇偶性由公式 sin(-x)=-sin x图象关于原点成中心对称 .正弦函数是奇函数.新授在闭区间 上, 是增函数; (4) 正弦函数的单调性-1 0 1 0 -1在闭区间 上,是减函数.观察正弦函数图象新授1. 诱导公式.
2. 正弦曲线的五点作图法.
3. 填表:10-1010复习一、余弦函数的图象 余弦函数图象的五个关键点:与 x 轴的交点图象的最高点图象的最低点五点
作图法
新授 由诱导公式 cos( x+2k?)=cos x,将 y=cos x ,x?[0,2 ?] 的图象沿 x 轴向左、右平移2 ?, 4 ? ,…,
就可得到 y=cos x的图象.余 弦 曲 线 新授二、余弦函数的性质 定义域 x ? R ,值 域 y?[- 1, 1]. 当 x=2 k?,k ? Z 时,
y=cos x 取得最大值1,即 ymax=1;
当 x= (2 k+1) ? , k ? Z 时,
y=cos x 取得最小值 -1,即 ymin=-1. 观察余弦曲线(1) 余弦函数的值域新授 由公式 cos(x+k · 2? )=cos x ( k ? Z )
可知:
余弦函数是一个周期函数,2? ,4? ,…,-2? ,-4? ,… , 2k? ( k ? Z 且 k≠0 )
都是余弦函数的周期;
2? 是其最小正周期. (2) 余弦函数的周期 余弦函数的图象每隔 2? 重复出现. 新授(3) 余弦函数的奇偶性 由公式 cos(-x)=cos x 余弦函数是偶函数.图象关于 y 轴成轴对称 . 新授(4) 余弦函数的单调性 观察余弦曲线-1 0 1 0 -1在 [(2 k-1) ?, 2 k?] (k?Z)上,是增函数; 在 [2 k?,(2 k+1)? ] (k?Z)上,是减函数. 新授 正弦、余弦函数的图象 例1 画出函数y=1+sinx,x?[0, 2?]的简图:010-10 1 2 1 0 1 o1-12y=sinx,x?[0, 2?]y=1+sinx,x?[0, 2?]步骤:
1.列表
2.描点
3.连线例 2 求使函数 y=2+sin x 取最大值、最小值
的 x 的集合,并求出这个函数的最大值,
最小值和周期 T .解例题讲解 正弦、余弦函数的图象 y=sinx,x?[0, 2?]100-10 正弦、余弦函数的图象 正弦、余弦函数的图象 小
结1. 正弦曲线、余弦曲线2.注意与诱导公式、三角函数线等知识的联系y=sinx,x?[0, 2?]y=cosx,x?[0, 2?] 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 余弦曲线(0,1)( ? ,-1)( 2? ,1)正弦曲线形状完全一样只是位置不同
