湘教版七年级数学下册《6. 1.2中位数 》教学设计
文档属性
| 名称 | 湘教版七年级数学下册《6. 1.2中位数 》教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 31.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 10:01:22 | ||
图片预览

文档简介
中位数教学设计
教学目标
知识与技能
使学生在实际情境中认识、理解中位数的统计意义。会求数据的中位数,了解中位数与平均数的联系与区别。
过程与方法
能根据具体的问题选择适当的统计量来反映一组数据的一般水平。
情感、态度与价值观
感受统计在生活中的应用,增强统计意识,发展统计观念。
重点难点
重点:认识中位数,理解中位数的统计意义,并会计算中位数。
难点:根据数据的具体情况合理地选择统计量。
教学过程
一、情境导入
1、当你以后长大了去找工作,看到这样的两家公司在招聘员工,你会选择哪一家?
旭日公司招聘启示
为了发展壮大,我公司营销部欲招聘员工若干名。营销部工资待遇优厚,员工每月平均工资3000元以上,希望有识之士加盟。
-----旭日公司
朝阳公司招聘启示
为了开发市场,我公司市场部欲招聘员工若干名。市场部工资待遇优厚,员工每月平均工资2800元以上,希望有识之士加盟。
----朝阳公司
生:……
教师进一步引导,发掘学生做选择的各种依据。这个问题情境中出现的已知数是平均数,所以学生大多数选择旭日公司。教师要从另一个角度的数据来引出本节课的内容。“那么,当你走进这两家公司,了解到他们的工资报表以后,你会如何选择呢?”
旭日公司营销部员工5月的工资情况:
经理:6680元;会计:2800元;专员甲:2850元;专员乙:2695元;
员工甲:2100元;员工乙:2250元; 员工丙:1890元。
朝阳公司市场部员工5月的工资情况:
总监:4500元;会计:2800元; 调查员甲:2880元;调查员乙:2855元
员工甲:2100元;员工乙:2850元; 员工丙:1950元。
学生思考,然后交流讨论,学生代表说出他们的想法。
师置疑:这种情况下,平均数还能代表公司员工工资的一般水平吗?哪一个数才能更好地反映他们的一般工资水平?
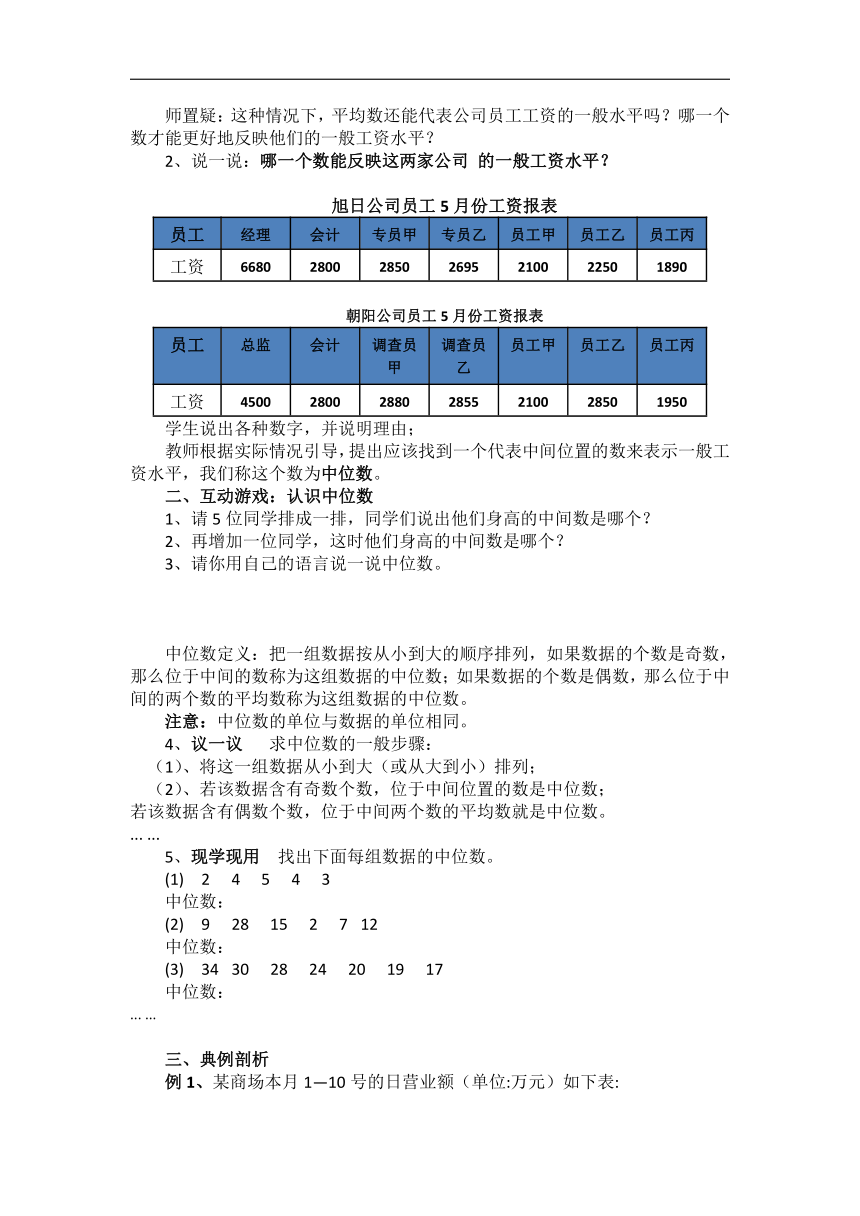
2、说一说:哪一个数能反映这两家公司 的一般工资水平?
旭日公司员工5月份工资报表
员工 经理 会计 专员甲 专员乙 员工甲 员工乙 员工丙
工资 6680 2800 2850 2695 2100 2250 1890
朝阳公司员工5月份工资报表
员工 总监 会计 调查员甲 调查员乙 员工甲 员工乙 员工丙
工资 4500 2800 2880 2855 2100 2850 1950
学生说出各种数字,并说明理由;
教师根据实际情况引导,提出应该找到一个代表中间位置的数来表示一般工资水平,我们称这个数为中位数。
二、互动游戏:认识中位数
1、请5位同学排成一排,同学们说出他们身高的中间数是哪个?
2、再增加一位同学,这时他们身高的中间数是哪个?
3、请你用自己的语言说一说中位数。
中位数定义:把一组数据按从小到大的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数。
注意:中位数的单位与数据的单位相同。
4、议一议 求中位数的一般步骤:
(1)、将这一组数据从小到大(或从大到小)排列;
(2)、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。
... ...
5、现学现用 找出下面每组数据的中位数。
(1) 2 4 5 4 3
中位数:
(2) 9 28 15 2 7 12
中位数:
(3) 34 30 28 24 20 19 17
中位数:
... ...
三、典例剖析
例1、某商场本月1—10号的日营业额(单位:万元)如下表:
日期 1 2 3 4 5 6 7 8 9 10
日营业额(万元) 5.3 6.2 3.6 4.5 8.6 6.8 4.5 6.3 6.5 6.6
(1)、请求出这10天日常营业额的平均数和中位数
解:(1)这10天的的日营业额的平均数为……5.89
将这组数据由小到大的顺序排列为:
3.6, 4.5, 4.5,5.3, 6.2, 6.3, 6.5, 6.6, 6.8, 8.6
处于中间位置的两个数据为:6.2和6.3
这组数据的中位数为……6.25(万元)
(2)、如果1—9号的日营业额不变,10日这一天的的日营业额变为16.6万元,那么这10天的日营业额的平均数和中位数是多少?
解:(2)这10天的的日营业额的平均数为……6.89
将这组数据由小到大的顺序排列为:
3.6, 4.5, 4.5,5.3, 6.2, 6.3, 6.5, 6.8, 8.6,16.6
处于中间位置的两个数据为:6.2和6.3
这组数据的中位数为……6.25(万元)
(3)、 请你对该商场本月2号的营业情况作出评价。
该商场本月2号的营业额为6.2万元,高于该月1—10号的日平均营业额,因而营业情况还是不错的,但是,该天的营业额略低于1—10号日营业额的中位数,这说明该天的营业额在这10天中,处于中等偏下水平。
想一想:平均数、中位数的区别
区别:
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值(偏大数或偏小数)的影响。但它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。不受极端值的影响。但不能充分利用所有的数据信息。
... ...
四、小试牛刀
1、下列说法中:
(1)一组数据中的中位数只有一个。
(2)一组数据中的中位数可能是这组数据中的一个,也可能不是这组数据中的一个。
(3)在一组数据中,大于中位数的数据与小于中位数的数据的个数相等。
正确的说法有 。
2、已知数据1 , 3 , 2 ,x, 2的平均是3,则这组数据的中位数是 。
3、一组数据23 27 20 18 x 12 ,它的中位数是21,则x的值是 。
4、如果在一组数据中,23、25、28、22
出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的中位数分别是( )
A.26 B.24 C.25 D.27
5、 数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数为( )
学生数
答对题数
A. 8 B. 7 C. 9 D. 10
6、综合提升:这组数据的中位数可以是几?
6 8 10 18 a
如果8是中位数,a可以是(a≤8)
如果10是中位数,a可以是(a≥10)
如果a是中位数,a可以是(8≤a≤10)
五、交流反思
回顾这节课,你都有哪些的收获?
无论是今天我们认识的中位数,还是以前学习过的平均数,其实都只是一种数据代表的方法,一个看问题的角度。面对纷繁复杂的事物还需要我们擦亮眼睛、小心选择,具体问题、具体分析。
六、布置作业
1、数据8、9、9、8、10、8、99、8、10、7、9、9、8的中位数是 。
2、随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) 5 7 10 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1)、该组数据的中位数是什么?
(2)、若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
教学目标
知识与技能
使学生在实际情境中认识、理解中位数的统计意义。会求数据的中位数,了解中位数与平均数的联系与区别。
过程与方法
能根据具体的问题选择适当的统计量来反映一组数据的一般水平。
情感、态度与价值观
感受统计在生活中的应用,增强统计意识,发展统计观念。
重点难点
重点:认识中位数,理解中位数的统计意义,并会计算中位数。
难点:根据数据的具体情况合理地选择统计量。
教学过程
一、情境导入
1、当你以后长大了去找工作,看到这样的两家公司在招聘员工,你会选择哪一家?
旭日公司招聘启示
为了发展壮大,我公司营销部欲招聘员工若干名。营销部工资待遇优厚,员工每月平均工资3000元以上,希望有识之士加盟。
-----旭日公司
朝阳公司招聘启示
为了开发市场,我公司市场部欲招聘员工若干名。市场部工资待遇优厚,员工每月平均工资2800元以上,希望有识之士加盟。
----朝阳公司
生:……
教师进一步引导,发掘学生做选择的各种依据。这个问题情境中出现的已知数是平均数,所以学生大多数选择旭日公司。教师要从另一个角度的数据来引出本节课的内容。“那么,当你走进这两家公司,了解到他们的工资报表以后,你会如何选择呢?”
旭日公司营销部员工5月的工资情况:
经理:6680元;会计:2800元;专员甲:2850元;专员乙:2695元;
员工甲:2100元;员工乙:2250元; 员工丙:1890元。
朝阳公司市场部员工5月的工资情况:
总监:4500元;会计:2800元; 调查员甲:2880元;调查员乙:2855元
员工甲:2100元;员工乙:2850元; 员工丙:1950元。
学生思考,然后交流讨论,学生代表说出他们的想法。
师置疑:这种情况下,平均数还能代表公司员工工资的一般水平吗?哪一个数才能更好地反映他们的一般工资水平?
2、说一说:哪一个数能反映这两家公司 的一般工资水平?
旭日公司员工5月份工资报表
员工 经理 会计 专员甲 专员乙 员工甲 员工乙 员工丙
工资 6680 2800 2850 2695 2100 2250 1890
朝阳公司员工5月份工资报表
员工 总监 会计 调查员甲 调查员乙 员工甲 员工乙 员工丙
工资 4500 2800 2880 2855 2100 2850 1950
学生说出各种数字,并说明理由;
教师根据实际情况引导,提出应该找到一个代表中间位置的数来表示一般工资水平,我们称这个数为中位数。
二、互动游戏:认识中位数
1、请5位同学排成一排,同学们说出他们身高的中间数是哪个?
2、再增加一位同学,这时他们身高的中间数是哪个?
3、请你用自己的语言说一说中位数。
中位数定义:把一组数据按从小到大的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数。
注意:中位数的单位与数据的单位相同。
4、议一议 求中位数的一般步骤:
(1)、将这一组数据从小到大(或从大到小)排列;
(2)、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。
... ...
5、现学现用 找出下面每组数据的中位数。
(1) 2 4 5 4 3
中位数:
(2) 9 28 15 2 7 12
中位数:
(3) 34 30 28 24 20 19 17
中位数:
... ...
三、典例剖析
例1、某商场本月1—10号的日营业额(单位:万元)如下表:
日期 1 2 3 4 5 6 7 8 9 10
日营业额(万元) 5.3 6.2 3.6 4.5 8.6 6.8 4.5 6.3 6.5 6.6
(1)、请求出这10天日常营业额的平均数和中位数
解:(1)这10天的的日营业额的平均数为……5.89
将这组数据由小到大的顺序排列为:
3.6, 4.5, 4.5,5.3, 6.2, 6.3, 6.5, 6.6, 6.8, 8.6
处于中间位置的两个数据为:6.2和6.3
这组数据的中位数为……6.25(万元)
(2)、如果1—9号的日营业额不变,10日这一天的的日营业额变为16.6万元,那么这10天的日营业额的平均数和中位数是多少?
解:(2)这10天的的日营业额的平均数为……6.89
将这组数据由小到大的顺序排列为:
3.6, 4.5, 4.5,5.3, 6.2, 6.3, 6.5, 6.8, 8.6,16.6
处于中间位置的两个数据为:6.2和6.3
这组数据的中位数为……6.25(万元)
(3)、 请你对该商场本月2号的营业情况作出评价。
该商场本月2号的营业额为6.2万元,高于该月1—10号的日平均营业额,因而营业情况还是不错的,但是,该天的营业额略低于1—10号日营业额的中位数,这说明该天的营业额在这10天中,处于中等偏下水平。
想一想:平均数、中位数的区别
区别:
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值(偏大数或偏小数)的影响。但它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。不受极端值的影响。但不能充分利用所有的数据信息。
... ...
四、小试牛刀
1、下列说法中:
(1)一组数据中的中位数只有一个。
(2)一组数据中的中位数可能是这组数据中的一个,也可能不是这组数据中的一个。
(3)在一组数据中,大于中位数的数据与小于中位数的数据的个数相等。
正确的说法有 。
2、已知数据1 , 3 , 2 ,x, 2的平均是3,则这组数据的中位数是 。
3、一组数据23 27 20 18 x 12 ,它的中位数是21,则x的值是 。
4、如果在一组数据中,23、25、28、22
出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的中位数分别是( )
A.26 B.24 C.25 D.27
5、 数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数为( )
学生数
答对题数
A. 8 B. 7 C. 9 D. 10
6、综合提升:这组数据的中位数可以是几?
6 8 10 18 a
如果8是中位数,a可以是(a≤8)
如果10是中位数,a可以是(a≥10)
如果a是中位数,a可以是(8≤a≤10)
五、交流反思
回顾这节课,你都有哪些的收获?
无论是今天我们认识的中位数,还是以前学习过的平均数,其实都只是一种数据代表的方法,一个看问题的角度。面对纷繁复杂的事物还需要我们擦亮眼睛、小心选择,具体问题、具体分析。
六、布置作业
1、数据8、9、9、8、10、8、99、8、10、7、9、9、8的中位数是 。
2、随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) 5 7 10 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1)、该组数据的中位数是什么?
(2)、若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
