湘教版七年级数学下册《4.1.2 相交直线所成的角》教学设计
文档属性
| 名称 | 湘教版七年级数学下册《4.1.2 相交直线所成的角》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 10:24:07 | ||
图片预览



文档简介
4.1.2 相交直线所成的角
教学目标:
1.理解相交直线所成的角意义,理解对顶角、同位角、内错角、同旁内角的概念。能准确地找出三条直线相交所构成的八个角的关系。
2.理解对顶角相等的性质。
3.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系。
教学难点:
准确找出三条直线相交所构成的八个角的关系,对顶角的性质及等量代换得到他们之间的等量关系
教学重点:
三条直线所构成的八个角的关系、对顶角的性质。
教学内容:
1、 对顶角
【自主学习】
(一)动手操作
观察思考:要求学生拿出事先准备好的纸和剪刀,用剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。两把手之间的角逐渐变大,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。
(2)自主探究
问题1:两条相交直线相交形成的四个角有什么位置关系?
(1)观察∠AOC与∠BOC,它们的位置有什么关系?它们的数量有什么关系?(引出邻补角定义)
(2)观察∠AOC与∠BOD,它们的位置有什么关系?有什么特点?(引出对顶角定义)
对顶角的定义:∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角叫做对顶角.
问题2:你所画的图形中还有哪些对顶角?
问题3:判断下列图形中哪对角是对顶角?
问题4:∠1与∠3有怎样的数量关系?你能说出∠1=∠3的道理吗?
解:因为 ∠1与∠2互补,
∠3与∠2互补(邻补角的定义)
所以∠1=∠3(同角的补角相等)
同理∠2=∠4 .
【应用】如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数。
2、 探究
问题1:∠1与∠3有怎样的数量关系?比较它们的大小(用自己喜欢的方式)。
你能说出∠1=∠3的道理吗?
解:因为 ∠1与∠2互补,
∠3与∠2互补(补角的定义),
所以 ∠1=∠3(同角的补角相等)
同理 ∠2=∠4 .
对顶角的性质:对顶角相等.
3、 探究“三线八角
我们来探究:两条直线被第三条直线所截,所构成的角中没有公共顶点的角之间的关系。
【合作交流】
如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截)构成 8 个角。现在,我们来研究其中没有公共顶点的两个角的关系。
(一)同位角
1、定义:如图,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 。而它们的图像可近似地看成英文字母“F”,具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成同位角?
3、两条直线被第三条直线所截构成的八个角中,共有 对同位角。
(二)内错角
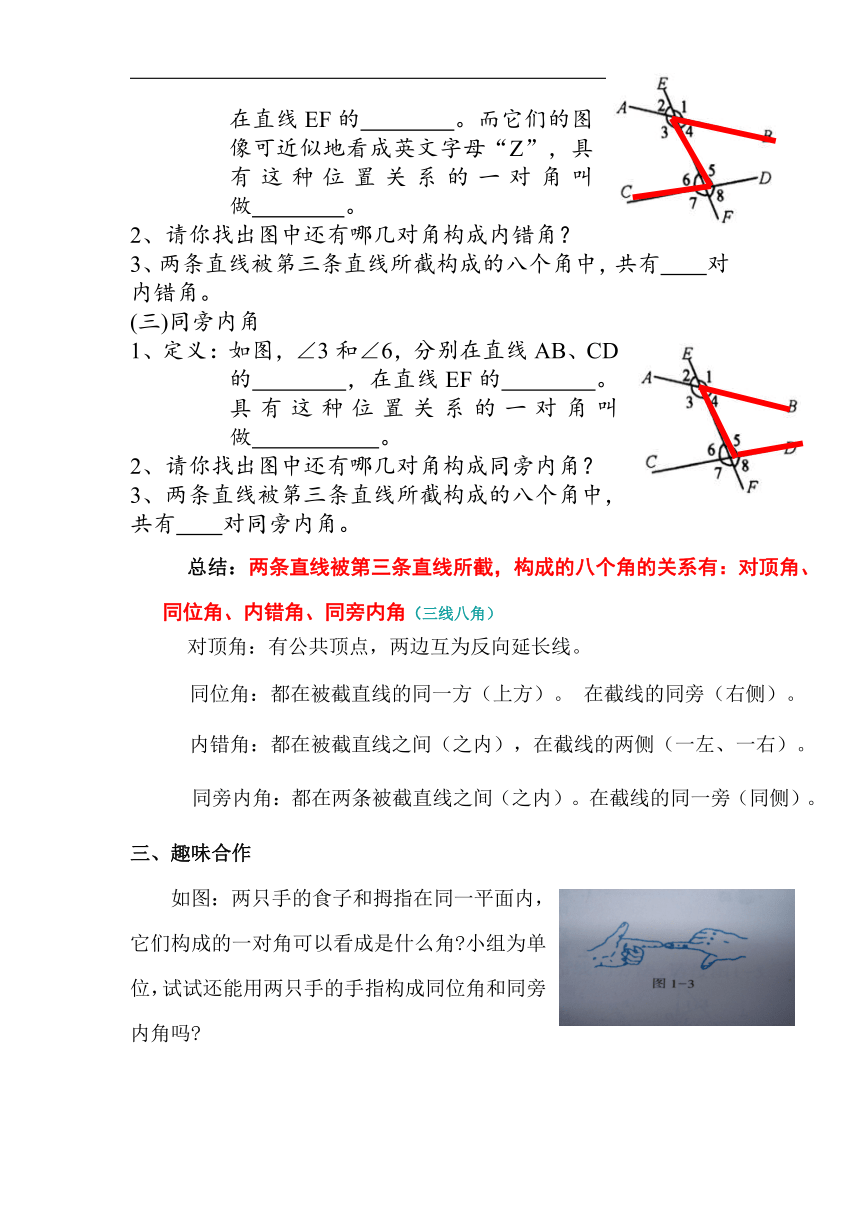
1、定义:如图,∠3和∠5,分别在直线AB、CD的 ,在直线EF的 。而它们的图像可近似地看成英文字母“Z”,具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成内错角?
3、两条直线被第三条直线所截构成的八个角中,共有 对内错角。
(三)同旁内角
1、定义:如图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成同旁内角?
3、两条直线被第三条直线所截构成的八个角中,共有 对同旁内角。
三、趣味合作
如图:两只手的食子和拇指在同一平面内,它们构成的一对角可以看成是什么角 小组为单位,试试还能用两只手的手指构成同位角和同旁内角吗
四、例题讲解
例1: 如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4, ∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2: 例2 如图,直线AB,CD被直线MN所截,同位角∠1 与∠2相等;
(1)那么内错角∠2与∠3相等吗?
(2)∠4与∠2具有怎样的数量关系?为什么?
深化概念,提升能力:
如果两条直线被第三条直线所截,下列三个条件中,只要其中的一个成立,则另外两个也成立。
(1)有一对同位角相等
(2)有一对内错角相等
(3)有一对同旁内角互补
3、练习
(1)如果把图看成是直线AB、EF被直线CD所截,那么∠1与∠2是一对什么角?∠3与∠4呢? ∠2与∠4呢?
解:∠1与∠2是同位角;∠3与∠4内错角;∠2与∠4是同旁内角
(2)直线a、b与直线c相交,设∠1=∠4=108°,求其他角的度数.
解:∠1与∠4,∠2与∠5是同位角;∠3与∠4是内错角;∠2与∠4是同旁内角. 因有一对同位角相等, 即∠1=∠4=108°,
所以∠3=∠4=108°;
∠2 = 180°-∠1 = 72°;
∠5 = 180°-∠4 = 72°.
5、扩展延伸
如图,AB、DC被BD所截得的内错角是 ,AD、BC被AC所截得的内错角是 ,∠ABC的同旁内角是 。
六、课堂小结
1. 你能总结一下对顶角、同位角、内错角、 同旁内角分别具有哪些特征吗?
2. 你认为在图形中识别对顶角、同位角、内错角、同旁内角的关键是什么?
3. 对顶角一定相等;同位角、内错角、同旁内角之间一定具有什么数量关系吗?
七、教学反思
本课设计旨在遵循从具体到抽象、从感性到理性的渐进认识规律,以启发探究式教学为主导,以学生熟悉的中国传统剪纸艺术引入课题,增加了学生的学习兴趣,让学生动手操作观察剪刀相对的角的大小变化,培养学生动手实践能力。
教师应发扬教学民主,成为学生数学活动的组织者、引导者和合作者。通过多媒体教学辅助手段,引导学生在活动中观察,启发学生用比较直观的语言来叙述邻补角和对顶角的概念,充分体现“数学教学主要是数学活动的教学”这一教育精神。在教学中充分发挥学生的直觉形象思维特点,让学生去发现同位角象“F”,内错角象“Z”,同旁内角象“U”,通过建立数学模型,有助于学生认识问题的本质。
本节课用手势表示同位角、内错角、同旁内角,学生表现出了极大的兴趣,大家都兴致盎然,其乐无穷。象这样采用多种方式调动学生的耳、眼、口、手多种感官共同参与活动,让学生既动脑又动手,既提高学生学习数学的兴趣,又加深了对数学知识的理解,使学生更进一步地参与数学、喜欢数学、热爱数学。
组织好小组合作学习,加强师生之间的互动,培养学生在独立思考问题的基础上,能够尊重与理解他人的意见,并培养与他人合作的能力。
1
2
1
2
1
2
总结:两条直线被第三条直线所截,构成的八个角的关系有:对顶角、同位角、内错角、同旁内角(三线八角)
同位角:都在被截直线的同一方(上方)。 在截线的同旁(右侧)。
内错角:都在被截直线之间(之内),在截线的两侧(一左、一右)。
同旁内角:都在两条被截直线之间(之内)。在截线的同一旁(同侧)。
对顶角:有公共顶点,两边互为反向延长线。
6
4
5
8
2
5
3
4
1
E
F
A
B
D
C
图3-47
教学目标:
1.理解相交直线所成的角意义,理解对顶角、同位角、内错角、同旁内角的概念。能准确地找出三条直线相交所构成的八个角的关系。
2.理解对顶角相等的性质。
3.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系。
教学难点:
准确找出三条直线相交所构成的八个角的关系,对顶角的性质及等量代换得到他们之间的等量关系
教学重点:
三条直线所构成的八个角的关系、对顶角的性质。
教学内容:
1、 对顶角
【自主学习】
(一)动手操作
观察思考:要求学生拿出事先准备好的纸和剪刀,用剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。两把手之间的角逐渐变大,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。
(2)自主探究
问题1:两条相交直线相交形成的四个角有什么位置关系?
(1)观察∠AOC与∠BOC,它们的位置有什么关系?它们的数量有什么关系?(引出邻补角定义)
(2)观察∠AOC与∠BOD,它们的位置有什么关系?有什么特点?(引出对顶角定义)
对顶角的定义:∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角叫做对顶角.
问题2:你所画的图形中还有哪些对顶角?
问题3:判断下列图形中哪对角是对顶角?
问题4:∠1与∠3有怎样的数量关系?你能说出∠1=∠3的道理吗?
解:因为 ∠1与∠2互补,
∠3与∠2互补(邻补角的定义)
所以∠1=∠3(同角的补角相等)
同理∠2=∠4 .
【应用】如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数。
2、 探究
问题1:∠1与∠3有怎样的数量关系?比较它们的大小(用自己喜欢的方式)。
你能说出∠1=∠3的道理吗?
解:因为 ∠1与∠2互补,
∠3与∠2互补(补角的定义),
所以 ∠1=∠3(同角的补角相等)
同理 ∠2=∠4 .
对顶角的性质:对顶角相等.
3、 探究“三线八角
我们来探究:两条直线被第三条直线所截,所构成的角中没有公共顶点的角之间的关系。
【合作交流】
如图,直线AB、CD与EF相交(或两条直线AB、CD被第三条直线EF所截)构成 8 个角。现在,我们来研究其中没有公共顶点的两个角的关系。
(一)同位角
1、定义:如图,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 。而它们的图像可近似地看成英文字母“F”,具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成同位角?
3、两条直线被第三条直线所截构成的八个角中,共有 对同位角。
(二)内错角
1、定义:如图,∠3和∠5,分别在直线AB、CD的 ,在直线EF的 。而它们的图像可近似地看成英文字母“Z”,具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成内错角?
3、两条直线被第三条直线所截构成的八个角中,共有 对内错角。
(三)同旁内角
1、定义:如图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 。具有这种位置关系的一对角叫做 。
2、请你找出图中还有哪几对角构成同旁内角?
3、两条直线被第三条直线所截构成的八个角中,共有 对同旁内角。
三、趣味合作
如图:两只手的食子和拇指在同一平面内,它们构成的一对角可以看成是什么角 小组为单位,试试还能用两只手的手指构成同位角和同旁内角吗
四、例题讲解
例1: 如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4, ∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2: 例2 如图,直线AB,CD被直线MN所截,同位角∠1 与∠2相等;
(1)那么内错角∠2与∠3相等吗?
(2)∠4与∠2具有怎样的数量关系?为什么?
深化概念,提升能力:
如果两条直线被第三条直线所截,下列三个条件中,只要其中的一个成立,则另外两个也成立。
(1)有一对同位角相等
(2)有一对内错角相等
(3)有一对同旁内角互补
3、练习
(1)如果把图看成是直线AB、EF被直线CD所截,那么∠1与∠2是一对什么角?∠3与∠4呢? ∠2与∠4呢?
解:∠1与∠2是同位角;∠3与∠4内错角;∠2与∠4是同旁内角
(2)直线a、b与直线c相交,设∠1=∠4=108°,求其他角的度数.
解:∠1与∠4,∠2与∠5是同位角;∠3与∠4是内错角;∠2与∠4是同旁内角. 因有一对同位角相等, 即∠1=∠4=108°,
所以∠3=∠4=108°;
∠2 = 180°-∠1 = 72°;
∠5 = 180°-∠4 = 72°.
5、扩展延伸
如图,AB、DC被BD所截得的内错角是 ,AD、BC被AC所截得的内错角是 ,∠ABC的同旁内角是 。
六、课堂小结
1. 你能总结一下对顶角、同位角、内错角、 同旁内角分别具有哪些特征吗?
2. 你认为在图形中识别对顶角、同位角、内错角、同旁内角的关键是什么?
3. 对顶角一定相等;同位角、内错角、同旁内角之间一定具有什么数量关系吗?
七、教学反思
本课设计旨在遵循从具体到抽象、从感性到理性的渐进认识规律,以启发探究式教学为主导,以学生熟悉的中国传统剪纸艺术引入课题,增加了学生的学习兴趣,让学生动手操作观察剪刀相对的角的大小变化,培养学生动手实践能力。
教师应发扬教学民主,成为学生数学活动的组织者、引导者和合作者。通过多媒体教学辅助手段,引导学生在活动中观察,启发学生用比较直观的语言来叙述邻补角和对顶角的概念,充分体现“数学教学主要是数学活动的教学”这一教育精神。在教学中充分发挥学生的直觉形象思维特点,让学生去发现同位角象“F”,内错角象“Z”,同旁内角象“U”,通过建立数学模型,有助于学生认识问题的本质。
本节课用手势表示同位角、内错角、同旁内角,学生表现出了极大的兴趣,大家都兴致盎然,其乐无穷。象这样采用多种方式调动学生的耳、眼、口、手多种感官共同参与活动,让学生既动脑又动手,既提高学生学习数学的兴趣,又加深了对数学知识的理解,使学生更进一步地参与数学、喜欢数学、热爱数学。
组织好小组合作学习,加强师生之间的互动,培养学生在独立思考问题的基础上,能够尊重与理解他人的意见,并培养与他人合作的能力。
1
2
1
2
1
2
总结:两条直线被第三条直线所截,构成的八个角的关系有:对顶角、同位角、内错角、同旁内角(三线八角)
同位角:都在被截直线的同一方(上方)。 在截线的同旁(右侧)。
内错角:都在被截直线之间(之内),在截线的两侧(一左、一右)。
同旁内角:都在两条被截直线之间(之内)。在截线的同一旁(同侧)。
对顶角:有公共顶点,两边互为反向延长线。
6
4
5
8
2
5
3
4
1
E
F
A
B
D
C
图3-47
