人教版 八年级下册 19.2.2 一次函数的解析式 教案
文档属性
| 名称 | 人教版 八年级下册 19.2.2 一次函数的解析式 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 49.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 00:00:00 | ||
图片预览

文档简介
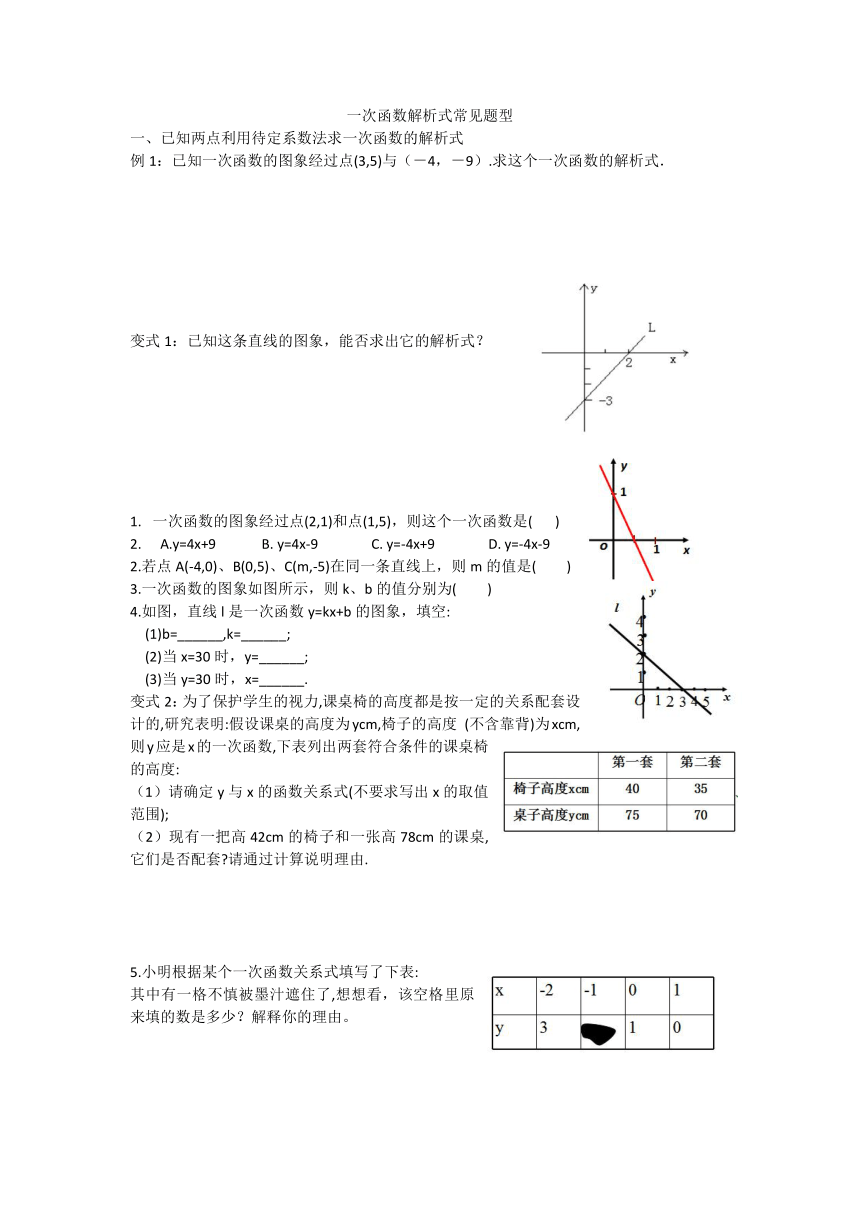
一次函数解析式常见题型
一、已知两点利用待定系数法求一次函数的解析式
例1:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
变式1:已知这条直线的图象,能否求出它的解析式?
一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9
2.若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
3.一次函数的图象如图所示,则k、b的值分别为( )
4.如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
变式2:为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度 (不含靠背)为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度:
(1)请确定y与x的函数关系式(不要求写出x的取值范围);
(2)现有一把高42cm的椅子和一张高78cm的课桌,它们是否配套 请通过计算说明理由.
5.小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
变式3:已知弹簧的长度y(厘米)在一定的限度内是所挂重物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.
6、为打赢脱贫攻坚战,一农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约90cm时,才开始开花结果,试问这种瓜苗移至大棚后,继续生长大约多少天,才开始开花结果?
二、已知一点利用待定系数法求一次函数的解析式
1、若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),你能求出这条直线的解析式吗?
2、已知一次函数y=kx+b的图象与y=2x平行且过点(2,-1),求这个一次函数解析式
3、已知一次函数y=kx+b的图象经过点(-2,4)且与直线y=3x垂直,求这个一次函数的解析式.
4、如图所示,直线l1与x轴交于点A,与y轴交于B,直线l2与直线l1关于y轴对称,且与x轴交于点C,已知直线l1的解析式为y=x+4.
(1)求直线l2的解析式;
(2)D为OC的中点,P是线段BC上一动点,求使OP+PD值最小的点P的坐标.
三、已知X与Y的关系求一次函数的解析式
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是
5.已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
四、由取值范围求一次函数的解析式
已知一次函数y=kx+b(k≠0)中,自变量x的取值范围是﹣2≤x≤6,函数值y的取值范围是﹣11≤y≤9,求个一次函数的解析式。
6.已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6,相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
五、知面积,求解析式
1、直线y=kx-2k与x轴交于点A,与y轴交于点B,且S△ABO=4,求直线AB的解析式。
2、已知直线y=kx-4与两坐标轴所围成的三角形面积等于4,求直线解析式.
一、已知两点利用待定系数法求一次函数的解析式
例1:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
变式1:已知这条直线的图象,能否求出它的解析式?
一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9
2.若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
3.一次函数的图象如图所示,则k、b的值分别为( )
4.如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
变式2:为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度 (不含靠背)为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度:
(1)请确定y与x的函数关系式(不要求写出x的取值范围);
(2)现有一把高42cm的椅子和一张高78cm的课桌,它们是否配套 请通过计算说明理由.
5.小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
变式3:已知弹簧的长度y(厘米)在一定的限度内是所挂重物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.
6、为打赢脱贫攻坚战,一农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约90cm时,才开始开花结果,试问这种瓜苗移至大棚后,继续生长大约多少天,才开始开花结果?
二、已知一点利用待定系数法求一次函数的解析式
1、若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),你能求出这条直线的解析式吗?
2、已知一次函数y=kx+b的图象与y=2x平行且过点(2,-1),求这个一次函数解析式
3、已知一次函数y=kx+b的图象经过点(-2,4)且与直线y=3x垂直,求这个一次函数的解析式.
4、如图所示,直线l1与x轴交于点A,与y轴交于B,直线l2与直线l1关于y轴对称,且与x轴交于点C,已知直线l1的解析式为y=x+4.
(1)求直线l2的解析式;
(2)D为OC的中点,P是线段BC上一动点,求使OP+PD值最小的点P的坐标.
三、已知X与Y的关系求一次函数的解析式
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是
5.已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
四、由取值范围求一次函数的解析式
已知一次函数y=kx+b(k≠0)中,自变量x的取值范围是﹣2≤x≤6,函数值y的取值范围是﹣11≤y≤9,求个一次函数的解析式。
6.已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6,相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
五、知面积,求解析式
1、直线y=kx-2k与x轴交于点A,与y轴交于点B,且S△ABO=4,求直线AB的解析式。
2、已知直线y=kx-4与两坐标轴所围成的三角形面积等于4,求直线解析式.
