2.2.1向量的加法运算及其几何意义(下)
文档属性
| 名称 | 2.2.1向量的加法运算及其几何意义(下) |  | |
| 格式 | zip | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-25 22:33:33 | ||
图片预览




文档简介
课件16张PPT。2.2.1向量的加法(下)湖南省耒阳市振兴学校
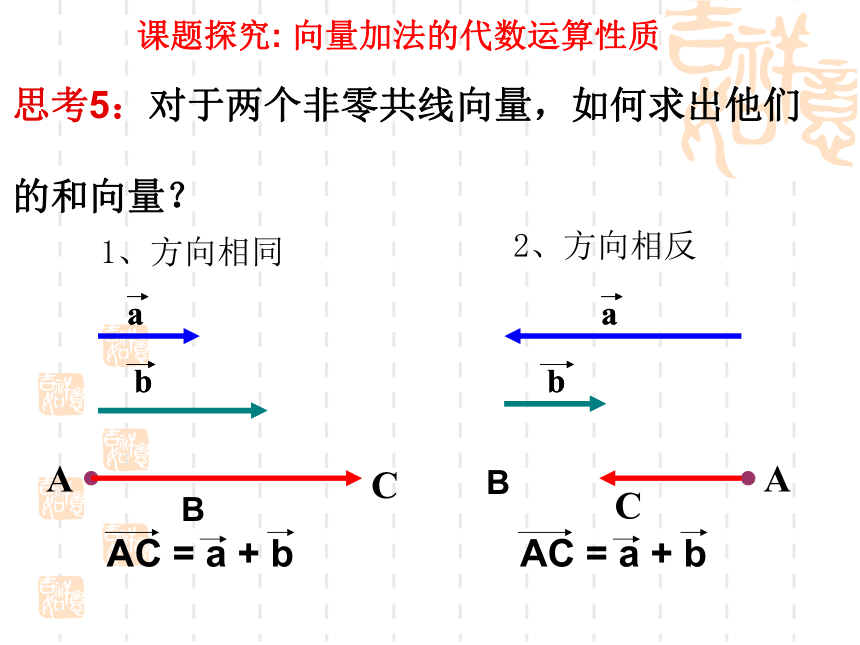
高中数学老师欧阳文丰制作1、向量加法的三角形法则(首尾相接,首尾连)复习巩固:2、向量加法的平行四边形法则(起点相同) 以第一个向量的终点作为第二个向量的起点,则由第一个向量的起点指向第二个向量的终点的向量就是和向量。 以同一起点的两个向量为邻边作平行四边形,则以公共起点为起点的对角线所对应向量就是和向量。思考5:对于两个非零共线向量,如何求出他们
的和向量?2、方向相反ABBACC1、方向相同课题探究: 向量加法的代数运算性质思考:1.若两向量互为相反向量,则它们的和为什么?3:若向量a与b同向,则向量a+b的方向如何?
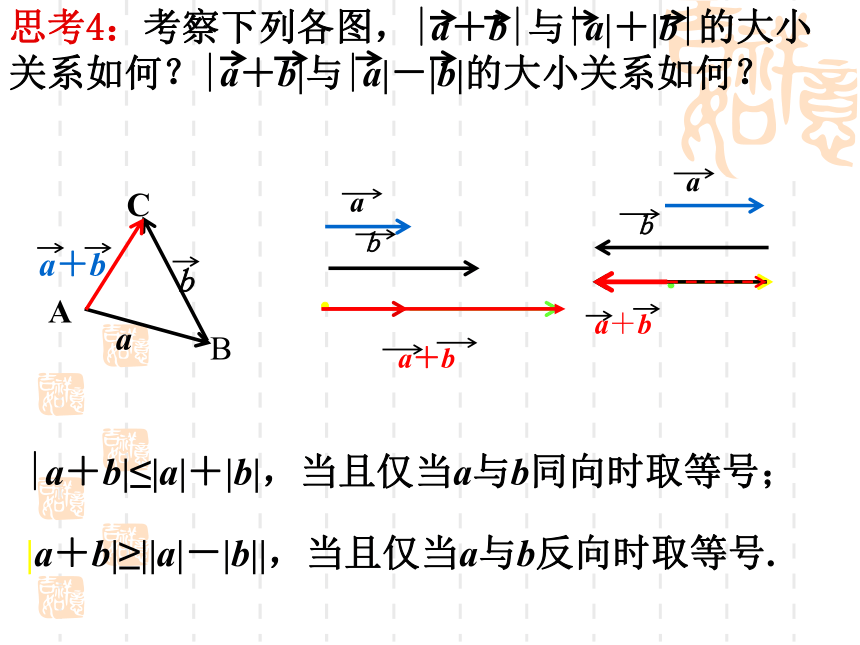
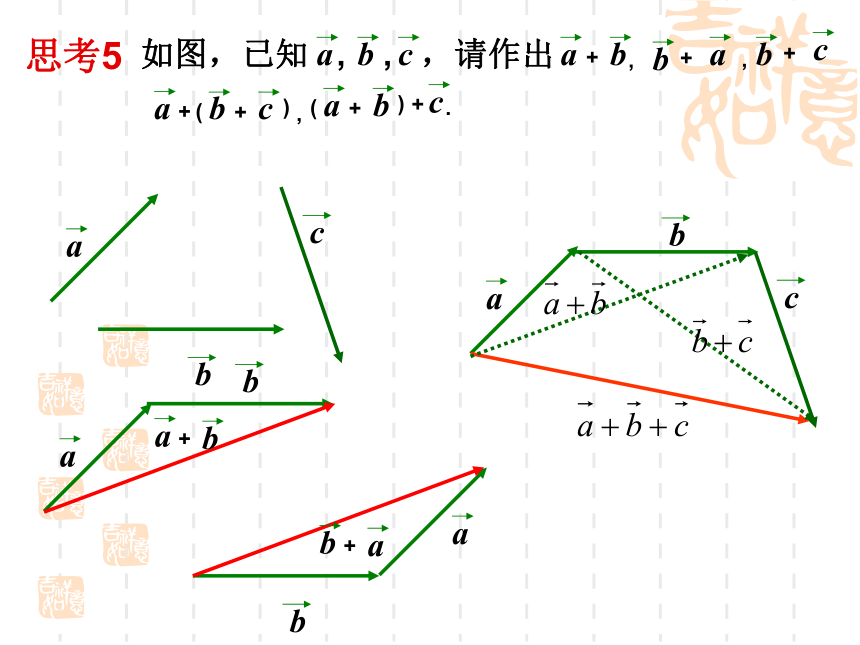
若向量a与b反向,则向量a+b的方向如何?ABCba+baaba+baba+b|a+b|≤|a|+|b|,当且仅当a与b同向时取等号;|a+b|≥||a|-|b||,当且仅当a与b反向时取等号.思考4:考察下列各图,|a+b|与|a|+|b|的大小关系如何?|a+b|与|a|-|b|的大小关系如何?思考5向量加法的运算律交换律:结合律:思考6: 等于什么向量?等于什么向量?探究A1A2A3An+1AnA4若平面内有n个首尾相接的向量,构成一个折线,那么这n个向量的和是多少呢?多边形法则探究A1A2A3AnAn-1A4若平面内有n个首尾相接的向量,构成一个封闭图形,那么这n个向量的和是多少呢?1.化简 例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以 km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)使用向量表示江水速度、船速以及船的实际航行的速度;
(2)求船实际航行速度的大小与方向.典型例题讲解解:如图,设用向量 表示船向垂直于对岸的速度,用向量 表示水流的速度答:船实际行驶速度的大小为4km/h,方向与水流速度间的夹角 .典型例题讲解课后思考练习题向 量 加 法 向 量 加 法课堂小结:向量加法的物理背景向量的加法运算向量加法的运算律平行四边形法则三角形法则向 量 加 法 向量加法实际应用作业:
P91习题2.2A组:1,2,3,4.
高中数学老师欧阳文丰制作1、向量加法的三角形法则(首尾相接,首尾连)复习巩固:2、向量加法的平行四边形法则(起点相同) 以第一个向量的终点作为第二个向量的起点,则由第一个向量的起点指向第二个向量的终点的向量就是和向量。 以同一起点的两个向量为邻边作平行四边形,则以公共起点为起点的对角线所对应向量就是和向量。思考5:对于两个非零共线向量,如何求出他们
的和向量?2、方向相反ABBACC1、方向相同课题探究: 向量加法的代数运算性质思考:1.若两向量互为相反向量,则它们的和为什么?3:若向量a与b同向,则向量a+b的方向如何?
若向量a与b反向,则向量a+b的方向如何?ABCba+baaba+baba+b|a+b|≤|a|+|b|,当且仅当a与b同向时取等号;|a+b|≥||a|-|b||,当且仅当a与b反向时取等号.思考4:考察下列各图,|a+b|与|a|+|b|的大小关系如何?|a+b|与|a|-|b|的大小关系如何?思考5向量加法的运算律交换律:结合律:思考6: 等于什么向量?等于什么向量?探究A1A2A3An+1AnA4若平面内有n个首尾相接的向量,构成一个折线,那么这n个向量的和是多少呢?多边形法则探究A1A2A3AnAn-1A4若平面内有n个首尾相接的向量,构成一个封闭图形,那么这n个向量的和是多少呢?1.化简 例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以 km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)使用向量表示江水速度、船速以及船的实际航行的速度;
(2)求船实际航行速度的大小与方向.典型例题讲解解:如图,设用向量 表示船向垂直于对岸的速度,用向量 表示水流的速度答:船实际行驶速度的大小为4km/h,方向与水流速度间的夹角 .典型例题讲解课后思考练习题向 量 加 法 向 量 加 法课堂小结:向量加法的物理背景向量的加法运算向量加法的运算律平行四边形法则三角形法则向 量 加 法 向量加法实际应用作业:
P91习题2.2A组:1,2,3,4.
