23.1.2 旋转作图 课件(共21张PPT)
文档属性
| 名称 | 23.1.2 旋转作图 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 17:24:19 | ||
图片预览






文档简介
(共21张PPT)
23.1.2 旋转作图
人教版九年级上册
教学目标
教学目标:1.掌握旋转及旋转作图的概念及基本性质.
2.能够根据旋转的基本性质解决实际问题和进行简单作图.
教学重点:会按照要求作出旋转后的图形.
教学难点:了解旋转角和旋转中心的改变可以得到不同效果的美丽的
图案,体验旋转在现实生活中的应用.
新知导入
情境引入
问题1:将线段 AB 绕点 O 顺时针旋转 90°.
A
B
O
A'
B'
作法:
1.将点A绕点O顺时针旋转90 ,得点A'
2.将点B绕点O顺时针旋转90 ,得点B'
3.连接A' B', 则线段A' B'即为所求.
线段的旋转作法
线段旋转的本质:找对应点
新知讲解
合作学习
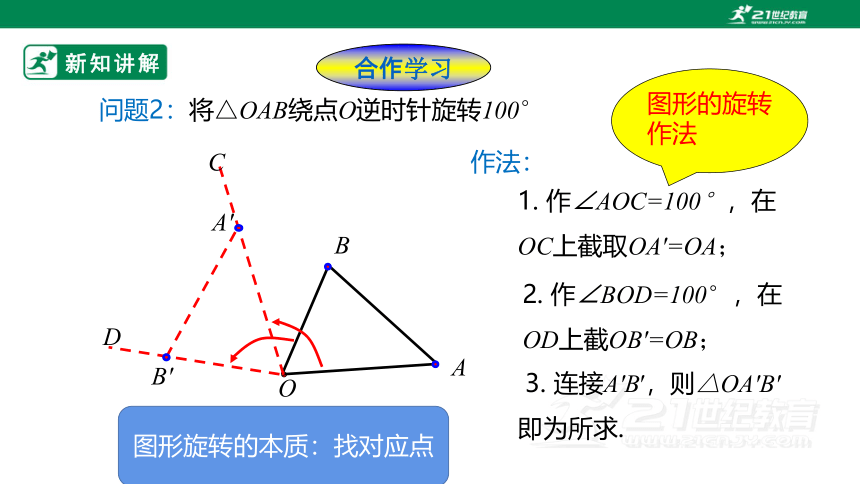
问题2:将△OAB绕点O逆时针旋转100°
B
A
O
A′
B′
1. 作∠AOC=100°,在OC上截取OA′=OA;
2. 作∠BOD=100°,在OD上截OB′=OB;
C
D
3. 连接A′B′,则△OA′B′即为所求.
作法:
图形的旋转作法
图形旋转的本质:找对应点
提炼概念
(1)审:明确旋转三要素:旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找:找出关键点(如顶点、中点、端点、圆心等等);
(3)作:作出关键点的对应点;
(4)画:画出新图形;
(5)写:写出结论.
典例精讲
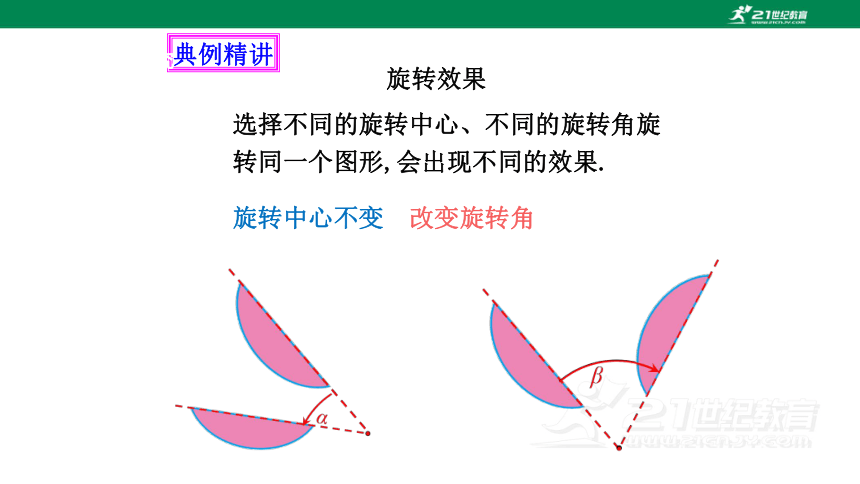
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形,会出现不同的效果.
旋转中心不变,改变旋转角
合作探究
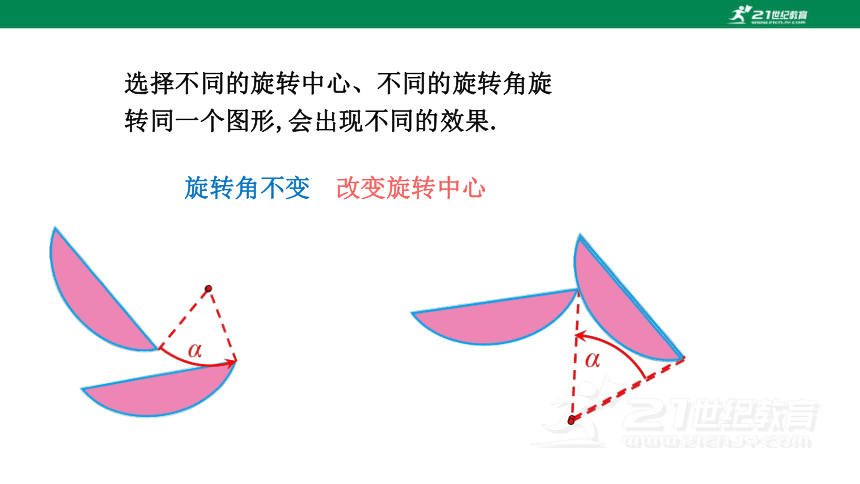
选择不同的旋转中心、不同的旋转角旋转同一个图形,会出现不同的效果.
旋转角不变,改变旋转中心
O1
O2
设计图案
我们可以借助旋转设计出许多美丽的图案.
课堂练习
1.如图,该图形围绕点O按下列角度旋转后,不能与自身重合的是( )
A.72° B.108°
C.144° D.216°
B
2.如图 ,正方形网格中, △MNP绕某点旋转一定的角度,得到△M1N1P1,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
N1
M1
N
M
P1
D
P
A
B
C
B
解析:作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
3.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,12)
B.(-2,0)
C.(2,12)或(-2,0)
D.(12,2)或(-2,0)
知识点拨:要注意分顺时针旋转和逆时针旋转两种情况讨论解答.
C
4. 如图是一个风车的轮廓,它可以看作是一个风叶经过几次旋转得到的 每次旋转了多少度 这个风车的形成还有哪些旋转方式
5. 如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
B
O
C
A
D
B
O
C
A
D
E
F
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形,
如图所示.
M
N
解:∵∠ABO=90°,∠A=30°,∴∠AOB=60°,
(1)若顺时针旋150°,如图,点 A′ 在 y 轴负半轴,
则 OA′=OA=4,
所以,点 A′ 的坐标为(0,-4);
6.如图,在△AOB中,AB⊥OB,∠A=30°,OA=4 ,将△OAB绕点O旋转150°得△OA'B',求点A'的坐标
(2)若逆时针旋150°,如图,点 A′ 在 第三象限,
则 OA′=OA=4,
所以,点 A′的坐标为( ,-2);
所以,点 A′的坐标为(0,-4)或( ,-2)
课堂总结
旋转
作图
作旋转图形
作图基本步骤五步
设计图案
改变旋转中心
改变旋转角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
23.1.2 旋转作图
人教版九年级上册
教学目标
教学目标:1.掌握旋转及旋转作图的概念及基本性质.
2.能够根据旋转的基本性质解决实际问题和进行简单作图.
教学重点:会按照要求作出旋转后的图形.
教学难点:了解旋转角和旋转中心的改变可以得到不同效果的美丽的
图案,体验旋转在现实生活中的应用.
新知导入
情境引入
问题1:将线段 AB 绕点 O 顺时针旋转 90°.
A
B
O
A'
B'
作法:
1.将点A绕点O顺时针旋转90 ,得点A'
2.将点B绕点O顺时针旋转90 ,得点B'
3.连接A' B', 则线段A' B'即为所求.
线段的旋转作法
线段旋转的本质:找对应点
新知讲解
合作学习
问题2:将△OAB绕点O逆时针旋转100°
B
A
O
A′
B′
1. 作∠AOC=100°,在OC上截取OA′=OA;
2. 作∠BOD=100°,在OD上截OB′=OB;
C
D
3. 连接A′B′,则△OA′B′即为所求.
作法:
图形的旋转作法
图形旋转的本质:找对应点
提炼概念
(1)审:明确旋转三要素:旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找:找出关键点(如顶点、中点、端点、圆心等等);
(3)作:作出关键点的对应点;
(4)画:画出新图形;
(5)写:写出结论.
典例精讲
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形,会出现不同的效果.
旋转中心不变,改变旋转角
合作探究
选择不同的旋转中心、不同的旋转角旋转同一个图形,会出现不同的效果.
旋转角不变,改变旋转中心
O1
O2
设计图案
我们可以借助旋转设计出许多美丽的图案.
课堂练习
1.如图,该图形围绕点O按下列角度旋转后,不能与自身重合的是( )
A.72° B.108°
C.144° D.216°
B
2.如图 ,正方形网格中, △MNP绕某点旋转一定的角度,得到△M1N1P1,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
N1
M1
N
M
P1
D
P
A
B
C
B
解析:作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
3.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,12)
B.(-2,0)
C.(2,12)或(-2,0)
D.(12,2)或(-2,0)
知识点拨:要注意分顺时针旋转和逆时针旋转两种情况讨论解答.
C
4. 如图是一个风车的轮廓,它可以看作是一个风叶经过几次旋转得到的 每次旋转了多少度 这个风车的形成还有哪些旋转方式
5. 如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
B
O
C
A
D
B
O
C
A
D
E
F
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形,
如图所示.
M
N
解:∵∠ABO=90°,∠A=30°,∴∠AOB=60°,
(1)若顺时针旋150°,如图,点 A′ 在 y 轴负半轴,
则 OA′=OA=4,
所以,点 A′ 的坐标为(0,-4);
6.如图,在△AOB中,AB⊥OB,∠A=30°,OA=4 ,将△OAB绕点O旋转150°得△OA'B',求点A'的坐标
(2)若逆时针旋150°,如图,点 A′ 在 第三象限,
则 OA′=OA=4,
所以,点 A′的坐标为( ,-2);
所以,点 A′的坐标为(0,-4)或( ,-2)
课堂总结
旋转
作图
作旋转图形
作图基本步骤五步
设计图案
改变旋转中心
改变旋转角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
