华师大版八年级上册11.2实数 课件(共19张PPT)
文档属性
| 名称 | 华师大版八年级上册11.2实数 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 651.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 17:01:35 | ||
图片预览





文档简介
(共19张PPT)
初中数学 八年级 上册
第十一章 第二节
实 数
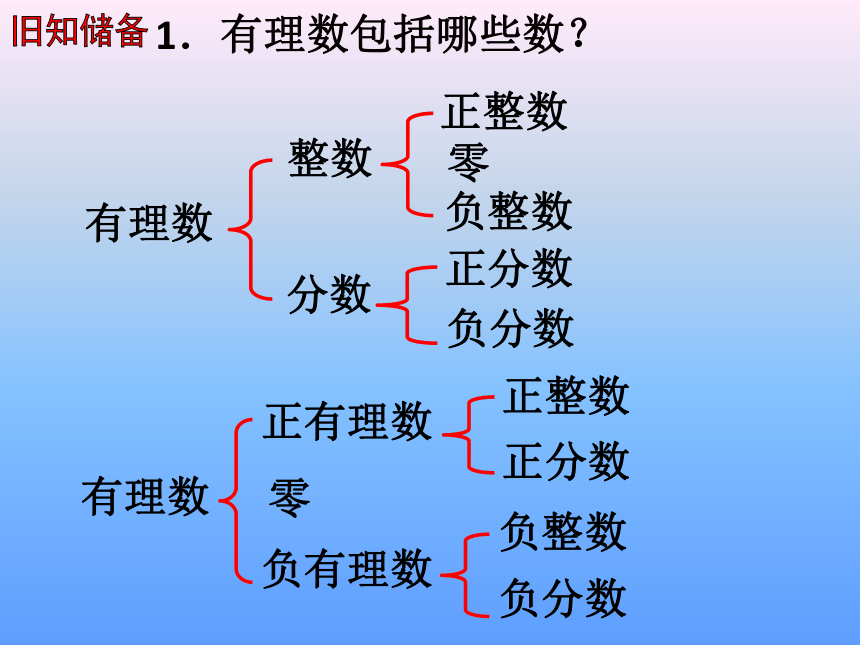
1.有理数包括哪些数?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
2.有理数中的分数能化为小数吗 化为什么样的小数?举例加以说明。
答:任何一个分数写成小数的形式,必是
有限小数或者无限循环小数
例如
是无限不循环小数。
=1.4142135623730950488016887242096980785696
71875376948073176679737990732478462107038
85038753432764157273501384623091229702492
48360558507372126441214970999358314132226
659275055927557999505011527820605715…
是怎样的数?
无限不循环的小数叫做无理数。
无理数:
无理数史话
大约公元600年,古希腊的毕达哥拉斯( Pythagoras) 学派认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,最后他遭到毕氏成员的追捕,被投入大海。
但真理是不可战胜的,后来古希腊人终于正视了希伯索斯的发现。关于无理数的发现是发现者付出了昂贵的代价的。他为真理而献出了宝贵的生命。
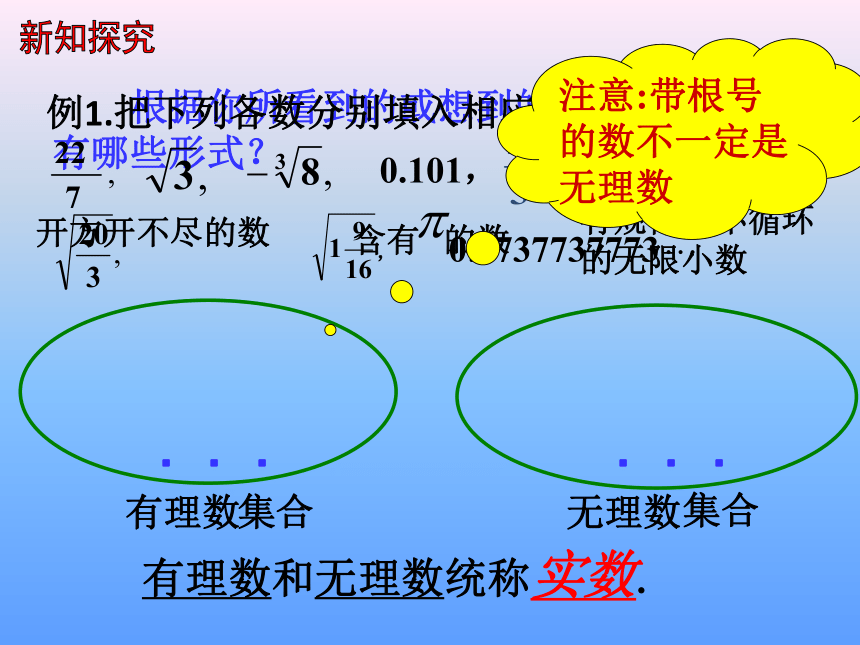
根据你所看到的或想到的,你觉得无理数都有哪些形式?
例1.把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
有理数和无理数统称实数.
...
...
开方开不尽的数
有规律但不循环
的无限小数
含有 的数
注意:带根号的数不一定是无理数
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
实数的分类:
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类:
例2. 把下列各数填入相应的集合内.
(1)无理数集合:{ …};
(2)有理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
你能在数轴上表示出 吗?
无理数能在数轴上表示出来吗?
0
-1
1
2
1
A
B
如图:OA=OB,数轴上A点对应的数是什么
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
你能在数轴上表示 吗?
实数和数轴上的点是一一对应的。
反过来,数轴上的每一点都表示一个实数。
每一个实数都可以用数轴上的一个点来表示;
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
8.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
×
×
×
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
7.两个无理数之和一定是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
练习1:填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
注意:在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
练习2:把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)
解:
在数轴上表示如下。
由上图得,
- <-1.4< <1.5<π<3.3
-2 -1 0 1 2 3 4 5
·
·
·
·
1.5
3.3
·
·
-1.4
在数轴上表示的两个实数,右边的数总比左边的数大。
…
实数
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
初中数学 八年级 上册
第十一章 第二节
实 数
1.有理数包括哪些数?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
2.有理数中的分数能化为小数吗 化为什么样的小数?举例加以说明。
答:任何一个分数写成小数的形式,必是
有限小数或者无限循环小数
例如
是无限不循环小数。
=1.4142135623730950488016887242096980785696
71875376948073176679737990732478462107038
85038753432764157273501384623091229702492
48360558507372126441214970999358314132226
659275055927557999505011527820605715…
是怎样的数?
无限不循环的小数叫做无理数。
无理数:
无理数史话
大约公元600年,古希腊的毕达哥拉斯( Pythagoras) 学派认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,最后他遭到毕氏成员的追捕,被投入大海。
但真理是不可战胜的,后来古希腊人终于正视了希伯索斯的发现。关于无理数的发现是发现者付出了昂贵的代价的。他为真理而献出了宝贵的生命。
根据你所看到的或想到的,你觉得无理数都有哪些形式?
例1.把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
有理数和无理数统称实数.
...
...
开方开不尽的数
有规律但不循环
的无限小数
含有 的数
注意:带根号的数不一定是无理数
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
实数的分类:
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类:
例2. 把下列各数填入相应的集合内.
(1)无理数集合:{ …};
(2)有理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
你能在数轴上表示出 吗?
无理数能在数轴上表示出来吗?
0
-1
1
2
1
A
B
如图:OA=OB,数轴上A点对应的数是什么
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
你能在数轴上表示 吗?
实数和数轴上的点是一一对应的。
反过来,数轴上的每一点都表示一个实数。
每一个实数都可以用数轴上的一个点来表示;
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
8.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
×
×
×
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
7.两个无理数之和一定是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
1.实数不是有理数就是无理数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
1.实数不是有理数就是无理数。( )
6.两个无理数之积不一定是无理数。( )
5.无理数一定都带根号。( )
4.带根号的数都是无理数。( )
3.无理数都是无限小数。( )
2. 无限小数都是无理数。( )
练习1:填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
注意:在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
练习2:把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)
解:
在数轴上表示如下。
由上图得,
- <-1.4< <1.5<π<3.3
-2 -1 0 1 2 3 4 5
·
·
·
·
1.5
3.3
·
·
-1.4
在数轴上表示的两个实数,右边的数总比左边的数大。
…
实数
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
