华师大版八年级上册13.2.3边角边课件(共20张PPT)
文档属性
| 名称 | 华师大版八年级上册13.2.3边角边课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 17:15:22 | ||
图片预览



文档简介
(共23张PPT)
三角形全等的判定
边角边
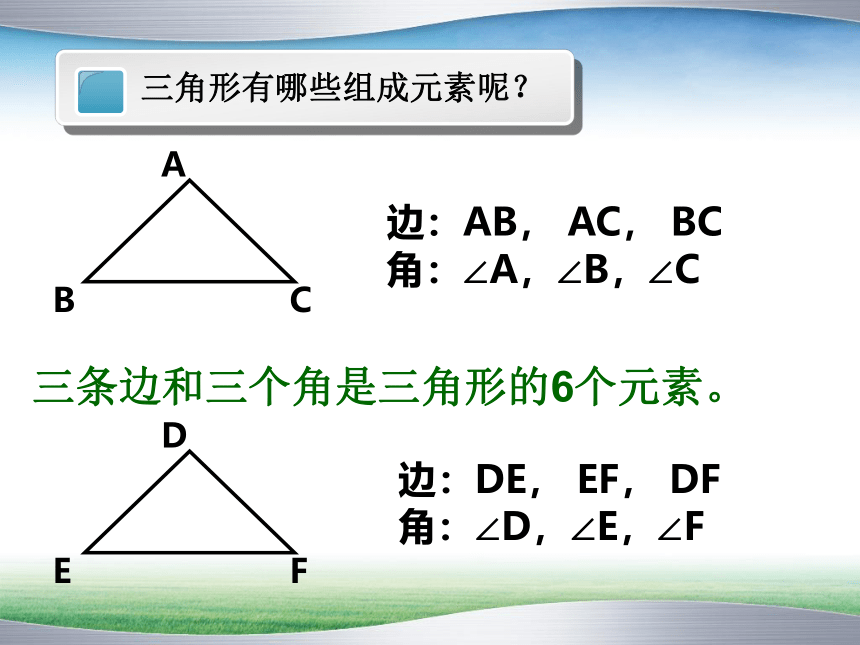
三条边和三个角是三角形的6个元素。
C
B
A
F
E
D
边:AB, AC, BC
角:∠A,∠B,∠C
边:DE, EF, DF
角:∠D,∠E,∠F
三角形有哪些组成元素呢?
A
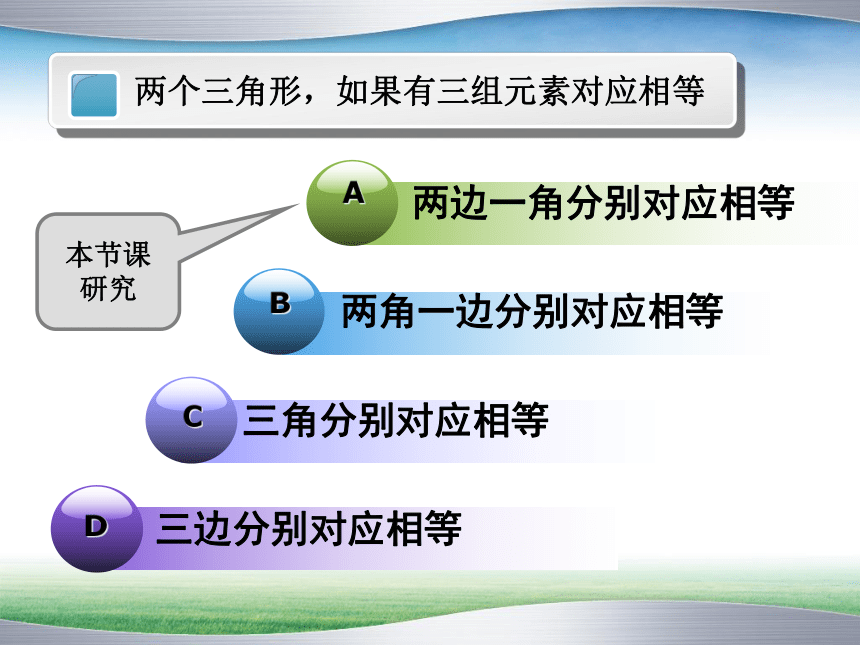
两边一角分别对应相等
本节课研究
B
两角一边分别对应相等
C
三角分别对应相等
D
三边分别对应相等
两个三角形,如果有三组元素对应相等
两边及其夹角
两边及一边对角
(边角边)
(边边角)
边角边
边边角
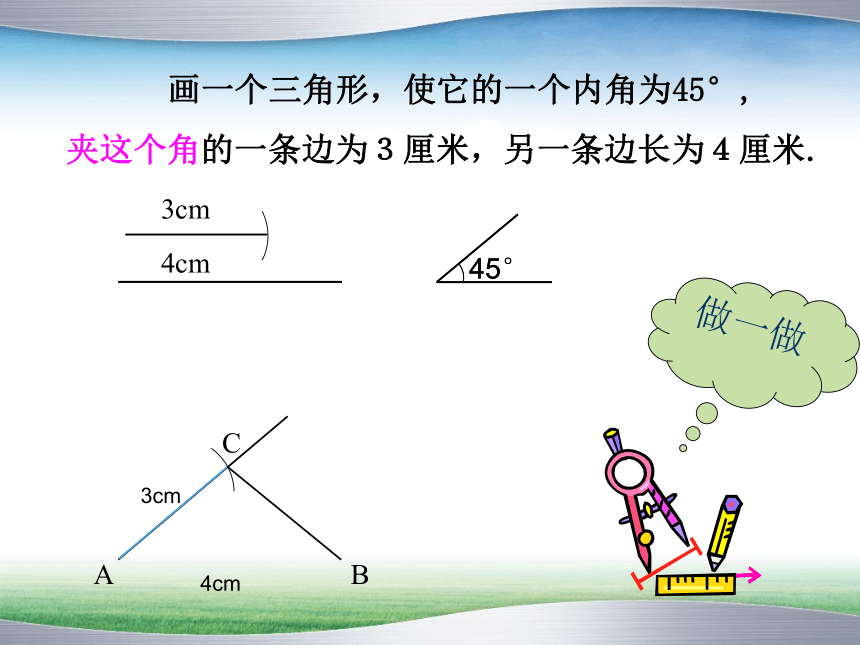
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
两边一角分别对应相等
4cm
3cm
45°
45°
C
B
A
4cm
3cm
画一个三角形,使它的一个内角为45°,
夹这个角的一条边为3厘米,另一条边长为4厘米.
做一做
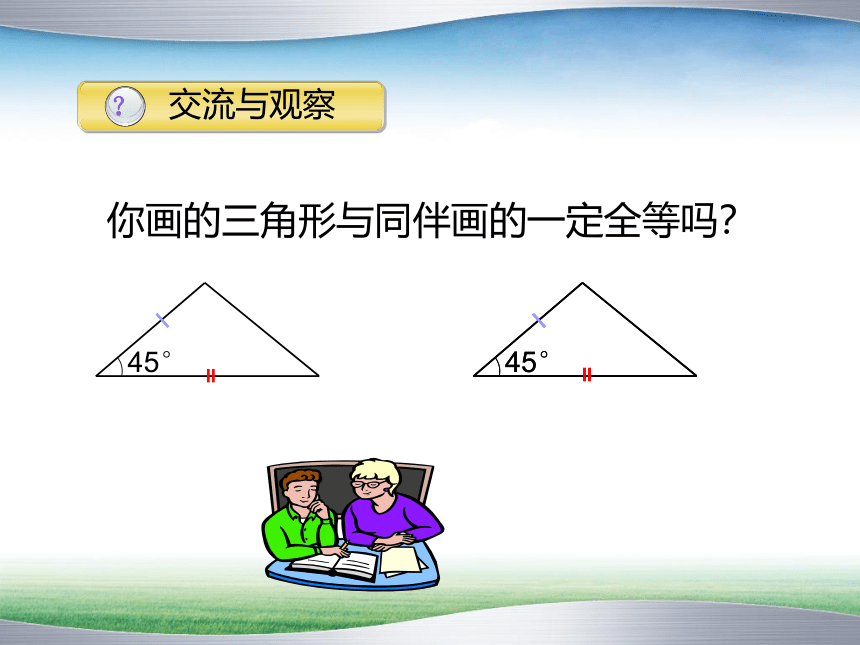
你画的三角形与同伴画的一定全等吗?
45°
45°
45°
交流与观察
?
一起来总结
如果两个三角形有两边及其夹角分别对应相等,
那么这两个三角形全等。
(简记为SAS)
要点
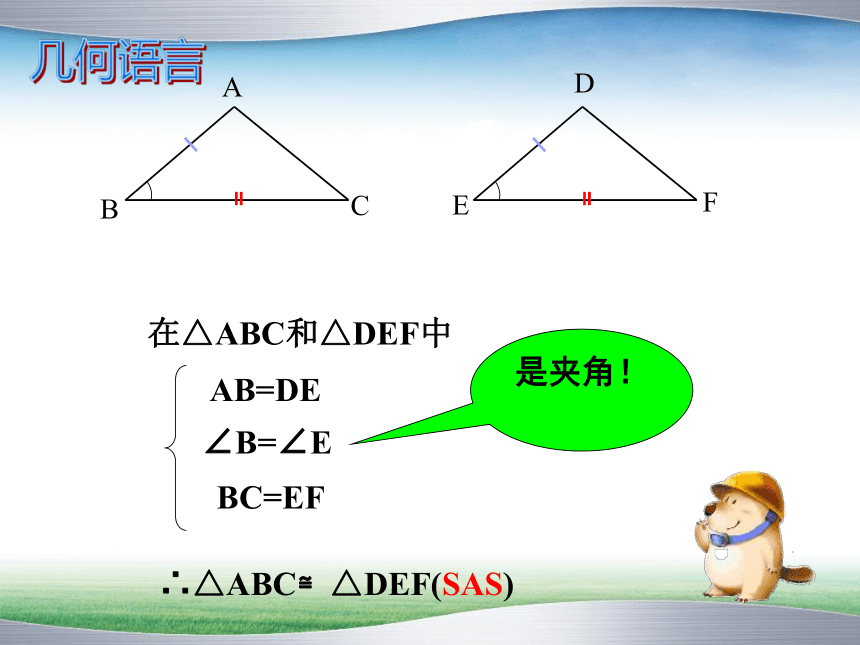
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
是夹角!
B
A
C
E
D
F
B
A
D
C
O
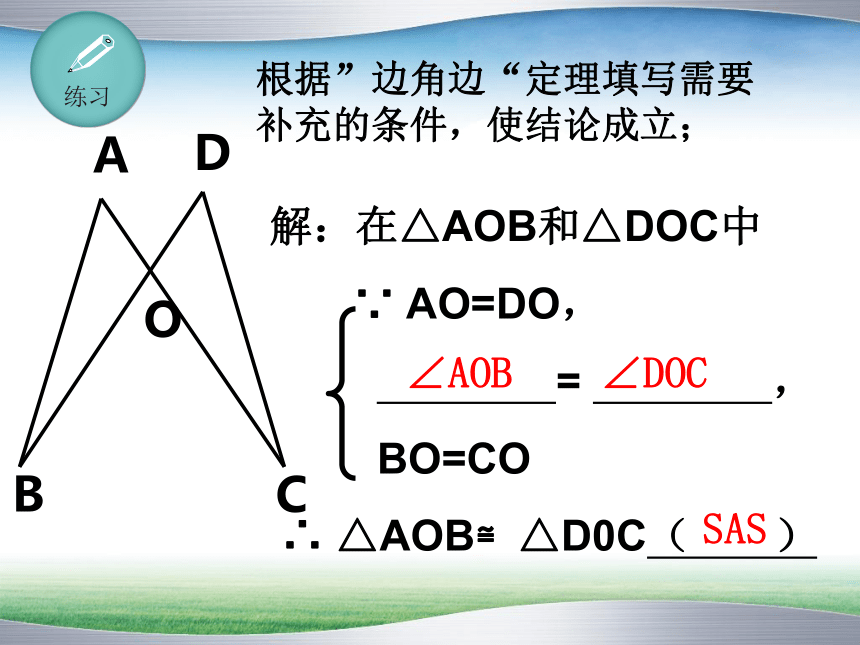
根据”边角边“定理填写需要补充的条件,使结论成立;
解:在△AOB和△DOC中
∵ AO=DO,
= ,
BO=CO
∴ △AOB≌△D0C( )
∠AOB ∠DOC
SAS
练习
≌
AB DC
练习
以3cm,4cm为三角形的两边,长度为3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
3cm
4cm
45°
45°
4cm
3cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
两边及其夹角
两边及一边对角
(边角边)
(边边角)
两边一角分别对应相等
边角边
边边角
(可判别)
(不能判别)
要点
若AB=AC
则添加什么条件可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD= ∠ CAD
练习
若∠BAD= ∠CAD则添加什么条件可使ΔABD≌ΔACD
A
B
D
C
ΔABD≌ΔACD
S
A
S
AD=AD
∠BAD= ∠ CAD
AB=AC
练习
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (S.A.S)
解:在△OAD 和△OBC中
C
B
A
D
O
2
1
例1
如图,已知AB和CD相交与O,
OA=OB, OC=OD.
说明 △ OAD与△ OBC全等的理由
例2
如图,点A,B,C,D在同一条直线上,
AB=CD,∠D=∠ECA,EC=FD
请说明:AE=BF
AC = BD
∠ECA =∠D(已知)
EC = FD (已知)
∴ △ACE ≌△BDF (S.A.S)
解:∵AB=CD
∴AC=BD
在△ACE 和△BDF中
∴ AE =BF
如图,AB=AE,∠B=∠E,BC=DE,点F是CD的中点.试说明:AF⊥CD.
证明:连接AC,AD
在△ABC和△AED中:
AB=AE(已知)
∠B=∠E(已知)
BC=DE(已知)
∴ △ABC≌ △AE(S.A.S)
∴ AC=AD(全等三角形对应边相等)
又∵点F是CD的中点
∴AF⊥CD(等腰三角形三线合一)
练习
如图,已知,AB=AC,AD=AE,∠BAE=∠CAD
试说明:∠B=∠C
练习
(2)连结BE,你还能得到什么结论 请写出来.(不要求说明理由)
练习
课堂小结:
如果两个三角形有两边及其夹角分别
SSA不成立
对应相等,那么这两个三角形全等。
简记为(SAS)
三角形全等的判定
边角边
三条边和三个角是三角形的6个元素。
C
B
A
F
E
D
边:AB, AC, BC
角:∠A,∠B,∠C
边:DE, EF, DF
角:∠D,∠E,∠F
三角形有哪些组成元素呢?
A
两边一角分别对应相等
本节课研究
B
两角一边分别对应相等
C
三角分别对应相等
D
三边分别对应相等
两个三角形,如果有三组元素对应相等
两边及其夹角
两边及一边对角
(边角边)
(边边角)
边角边
边边角
如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?
两边一角分别对应相等
4cm
3cm
45°
45°
C
B
A
4cm
3cm
画一个三角形,使它的一个内角为45°,
夹这个角的一条边为3厘米,另一条边长为4厘米.
做一做
你画的三角形与同伴画的一定全等吗?
45°
45°
45°
交流与观察
?
一起来总结
如果两个三角形有两边及其夹角分别对应相等,
那么这两个三角形全等。
(简记为SAS)
要点
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
是夹角!
B
A
C
E
D
F
B
A
D
C
O
根据”边角边“定理填写需要补充的条件,使结论成立;
解:在△AOB和△DOC中
∵ AO=DO,
= ,
BO=CO
∴ △AOB≌△D0C( )
∠AOB ∠DOC
SAS
练习
≌
AB DC
练习
以3cm,4cm为三角形的两边,长度为3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
3cm
4cm
45°
45°
4cm
3cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
两边及其夹角
两边及一边对角
(边角边)
(边边角)
两边一角分别对应相等
边角边
边边角
(可判别)
(不能判别)
要点
若AB=AC
则添加什么条件可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD= ∠ CAD
练习
若∠BAD= ∠CAD则添加什么条件可使ΔABD≌ΔACD
A
B
D
C
ΔABD≌ΔACD
S
A
S
AD=AD
∠BAD= ∠ CAD
AB=AC
练习
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (S.A.S)
解:在△OAD 和△OBC中
C
B
A
D
O
2
1
例1
如图,已知AB和CD相交与O,
OA=OB, OC=OD.
说明 △ OAD与△ OBC全等的理由
例2
如图,点A,B,C,D在同一条直线上,
AB=CD,∠D=∠ECA,EC=FD
请说明:AE=BF
AC = BD
∠ECA =∠D(已知)
EC = FD (已知)
∴ △ACE ≌△BDF (S.A.S)
解:∵AB=CD
∴AC=BD
在△ACE 和△BDF中
∴ AE =BF
如图,AB=AE,∠B=∠E,BC=DE,点F是CD的中点.试说明:AF⊥CD.
证明:连接AC,AD
在△ABC和△AED中:
AB=AE(已知)
∠B=∠E(已知)
BC=DE(已知)
∴ △ABC≌ △AE(S.A.S)
∴ AC=AD(全等三角形对应边相等)
又∵点F是CD的中点
∴AF⊥CD(等腰三角形三线合一)
练习
如图,已知,AB=AC,AD=AE,∠BAE=∠CAD
试说明:∠B=∠C
练习
(2)连结BE,你还能得到什么结论 请写出来.(不要求说明理由)
练习
课堂小结:
如果两个三角形有两边及其夹角分别
SSA不成立
对应相等,那么这两个三角形全等。
简记为(SAS)
