新版华东师大版2022年春七年级数学下册 6.2.1 等式的基本性质 课件(共21张PPT)
文档属性
| 名称 | 新版华东师大版2022年春七年级数学下册 6.2.1 等式的基本性质 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 22:41:02 | ||
图片预览






文档简介
(共21张PPT)
6.2 解一元一次方程
第6章 一元一次方程
第1课时 等式的性质
1
课堂讲解
等式的基本性质1
等式的基本性质2
方程的变形规则
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
等式的基本性质1
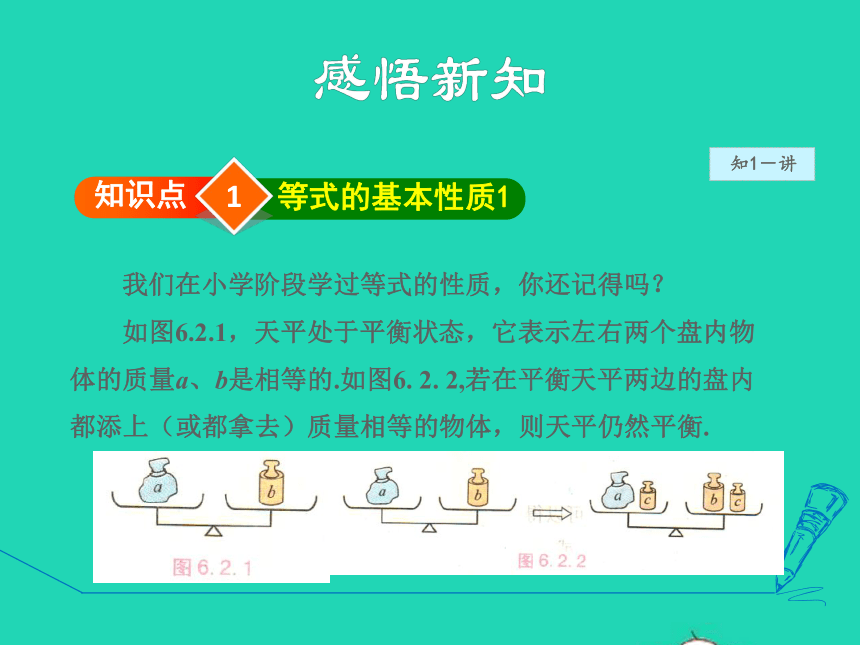
我们在小学阶段学过等式的性质,你还记得吗?
如图6.2.1,天平处于平衡状态,它表示左右两个盘内物
体的质量a、b是相等的.如图6. 2. 2,若在平衡天平两边的盘内
都添上(或都拿去)质量相等的物体,则天平仍然平衡.
知1-讲
知1-讲
总 结
这个事实反映了等式的基本性质1:
等式两边都加上(或都减去)同一个数或同一个整式,
所得结果仍是等式.
如果 a=b,那么 a+c=b+c,a-c=b-c.
例1
根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果4x=x-2,那么4x-___=-2( );
(2)如果2x+9=1,那么2x=1-____( );
知1-讲
导引:
(1)中方程的右边由x-2到-2,减了x,所以左边
也要减x;
(2)中方程的左边由2x+9到2x,减了9,所以右边
也要减9;
x
等式的性质1
9
等式的性质1
知1-讲
总 结
解答这类题一般是从已变化的一边入手,看它是
怎样从原等式变形到变形后的等式(如(1)中它是怎样从
x-2到-2),再把另一边也以同样的方式进行变形.
知1-练
1 填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(1)如果x-2=5,那么x=5+_____;
(2)如果 3x=10-2x,那么 3x+_____=10.
2 已知m+a=n+b,根据等式性质变形为m=n,那么a,b必须符合的条件是( )
A.a=-b B.ab=1
C.a=b D.a,b可以是任意整式
知1-练
3 下列各种变形中,不正确的是( )
A.从2+x=5可得到x=5-2
B.从3x=2x-1可得到3x-2x=-1
C.从5x=4x+1可得到4x-5x=1
D.从6x-2x=-3可得到6x=2x-3
2
知识点
等式的基本性质2
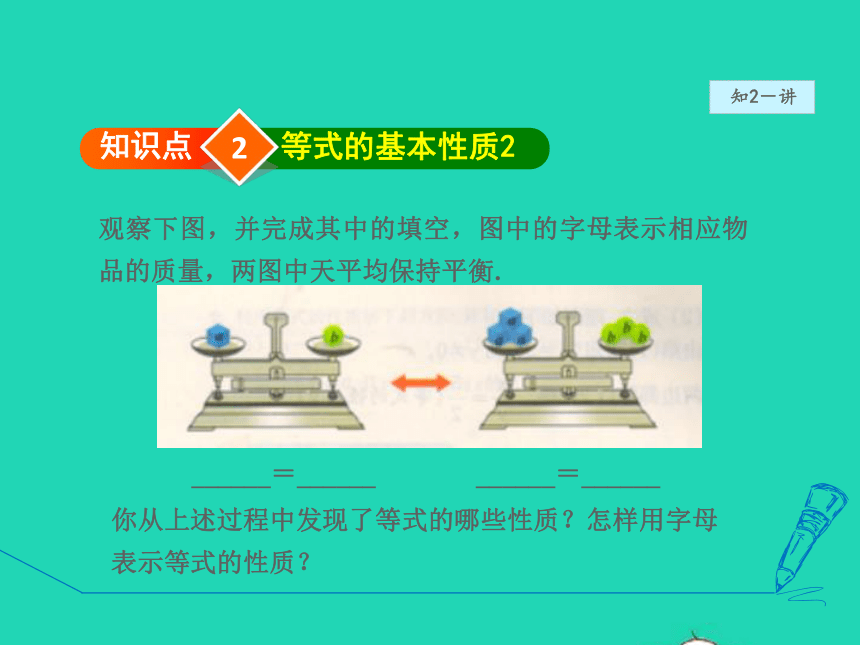
观察下图,并完成其中的填空,图中的字母表示相应物品的质量,两图中天平均保持平衡.
知2-讲
______=______
______=______
你从上述过程中发现了等式的哪些性质?怎样用字母
表示等式的性质?
知2-讲
总 结
等式的性质2
等式两边都乘以(或都除以)同一个数(除数不能为0),
所得结果仍是等式.
如果 a=b,那么 ac=bc, (c≠0).
例2
根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果- = ,那么x=____( );
(2)如果0.4a=3b,那么a=____( ).
知2-讲
导引:
(1)中方程的左边由- 到x,乘了-3,所以右边也
要乘-3;
(2)中方程的左边由0.4a到a除以了0.4,所以右边也
要除以0.4,即乘
等式的性质2
等式的性质2
知2-讲
总 结
等式的性质2中,除以的同一个数不能为0,并且
不能随便除以同一个式子.
知2-练
1 填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(1)如果2x=7,那么x=_____;
(2)如果 =3,那么x-1=_____.
2 等式2x-y=10变形为-4x+2y=-20的依据为( )
A.等式基本性质1 B.等式基本性质2
C.分数的基本性质 D.乘法分配律
知2-练
3 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 =x,那么2x+1-1=5x
3
知识点
方程的变形规则
知3-讲
利用等式的两个基本性质进行等式变形时,应
分析变形前、后式子的区别,发生加、减变形根据
等式的性质1,发生乘除变形的根据等式的性质2.
知3-讲
例3
〈易错题〉解方程:
(1)3x+1=10;(2)-8x=-6-7x;
(3) - +1= +2;(4)17y+5=10y-5-4y.
导引:
解方程就是经过移项、合并同类项、系数化为1
等适当的变形,最终得到x=a的形式.
知3-讲
(1)移项,得3x=10-1,合并同类项,得3x=9,
方程两边同除以3,得x=3.
(2)移项,得-8x+7x=-6,
合并同类项,得-x=-6,
方程两边同除以-1,得x=6.
(3)移项,得 =2-1,合并同类项,得
方程两边同除以 得x=
(4)移项,得17y-10y+4y=-5-5,合并同类项,
得11y=-10,方程两边同除以11,得y=
解:
知3-讲
总 结
移项时一般习惯将含未知数的项移到方程的左边,
常数项移到方程的右边.
知3-练
1 解方程:
(1)10=8+2x;
(2)
(3)
(4)-2x+7+5x=8-2x+2.
知3-练
2 在方程的变形中,移项的依据是( )
A.加法交换律 B.加法结合律
C.方程的变形规则1 D.方程的变形规则2
3 下列各选项中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
利用等式的基本性质变形的过程是由一个等式变形到
另一个等式的过程,变形时应注意:
(1)等式两边都要参加运算,并且进行的是同一种运算;
(2)等式两边加减乘除的整式一定是同一个整式;
(3)除以的整式不能为0.
6.2 解一元一次方程
第6章 一元一次方程
第1课时 等式的性质
1
课堂讲解
等式的基本性质1
等式的基本性质2
方程的变形规则
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
等式的基本性质1
我们在小学阶段学过等式的性质,你还记得吗?
如图6.2.1,天平处于平衡状态,它表示左右两个盘内物
体的质量a、b是相等的.如图6. 2. 2,若在平衡天平两边的盘内
都添上(或都拿去)质量相等的物体,则天平仍然平衡.
知1-讲
知1-讲
总 结
这个事实反映了等式的基本性质1:
等式两边都加上(或都减去)同一个数或同一个整式,
所得结果仍是等式.
如果 a=b,那么 a+c=b+c,a-c=b-c.
例1
根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果4x=x-2,那么4x-___=-2( );
(2)如果2x+9=1,那么2x=1-____( );
知1-讲
导引:
(1)中方程的右边由x-2到-2,减了x,所以左边
也要减x;
(2)中方程的左边由2x+9到2x,减了9,所以右边
也要减9;
x
等式的性质1
9
等式的性质1
知1-讲
总 结
解答这类题一般是从已变化的一边入手,看它是
怎样从原等式变形到变形后的等式(如(1)中它是怎样从
x-2到-2),再把另一边也以同样的方式进行变形.
知1-练
1 填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(1)如果x-2=5,那么x=5+_____;
(2)如果 3x=10-2x,那么 3x+_____=10.
2 已知m+a=n+b,根据等式性质变形为m=n,那么a,b必须符合的条件是( )
A.a=-b B.ab=1
C.a=b D.a,b可以是任意整式
知1-练
3 下列各种变形中,不正确的是( )
A.从2+x=5可得到x=5-2
B.从3x=2x-1可得到3x-2x=-1
C.从5x=4x+1可得到4x-5x=1
D.从6x-2x=-3可得到6x=2x-3
2
知识点
等式的基本性质2
观察下图,并完成其中的填空,图中的字母表示相应物品的质量,两图中天平均保持平衡.
知2-讲
______=______
______=______
你从上述过程中发现了等式的哪些性质?怎样用字母
表示等式的性质?
知2-讲
总 结
等式的性质2
等式两边都乘以(或都除以)同一个数(除数不能为0),
所得结果仍是等式.
如果 a=b,那么 ac=bc, (c≠0).
例2
根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果- = ,那么x=____( );
(2)如果0.4a=3b,那么a=____( ).
知2-讲
导引:
(1)中方程的左边由- 到x,乘了-3,所以右边也
要乘-3;
(2)中方程的左边由0.4a到a除以了0.4,所以右边也
要除以0.4,即乘
等式的性质2
等式的性质2
知2-讲
总 结
等式的性质2中,除以的同一个数不能为0,并且
不能随便除以同一个式子.
知2-练
1 填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(1)如果2x=7,那么x=_____;
(2)如果 =3,那么x-1=_____.
2 等式2x-y=10变形为-4x+2y=-20的依据为( )
A.等式基本性质1 B.等式基本性质2
C.分数的基本性质 D.乘法分配律
知2-练
3 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 =x,那么2x+1-1=5x
3
知识点
方程的变形规则
知3-讲
利用等式的两个基本性质进行等式变形时,应
分析变形前、后式子的区别,发生加、减变形根据
等式的性质1,发生乘除变形的根据等式的性质2.
知3-讲
例3
〈易错题〉解方程:
(1)3x+1=10;(2)-8x=-6-7x;
(3) - +1= +2;(4)17y+5=10y-5-4y.
导引:
解方程就是经过移项、合并同类项、系数化为1
等适当的变形,最终得到x=a的形式.
知3-讲
(1)移项,得3x=10-1,合并同类项,得3x=9,
方程两边同除以3,得x=3.
(2)移项,得-8x+7x=-6,
合并同类项,得-x=-6,
方程两边同除以-1,得x=6.
(3)移项,得 =2-1,合并同类项,得
方程两边同除以 得x=
(4)移项,得17y-10y+4y=-5-5,合并同类项,
得11y=-10,方程两边同除以11,得y=
解:
知3-讲
总 结
移项时一般习惯将含未知数的项移到方程的左边,
常数项移到方程的右边.
知3-练
1 解方程:
(1)10=8+2x;
(2)
(3)
(4)-2x+7+5x=8-2x+2.
知3-练
2 在方程的变形中,移项的依据是( )
A.加法交换律 B.加法结合律
C.方程的变形规则1 D.方程的变形规则2
3 下列各选项中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
利用等式的基本性质变形的过程是由一个等式变形到
另一个等式的过程,变形时应注意:
(1)等式两边都要参加运算,并且进行的是同一种运算;
(2)等式两边加减乘除的整式一定是同一个整式;
(3)除以的整式不能为0.
