18.1勾股定理 课件
图片预览




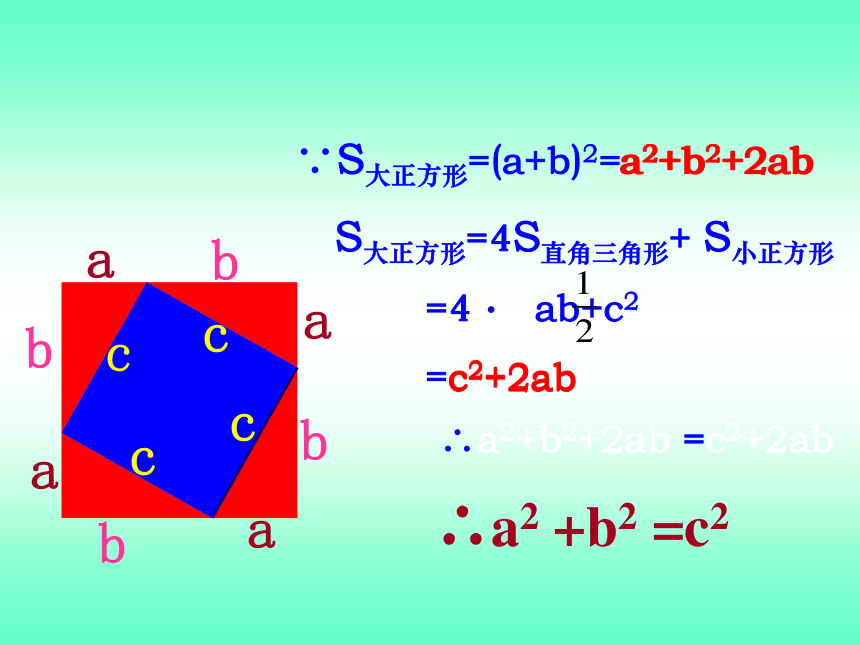
文档简介
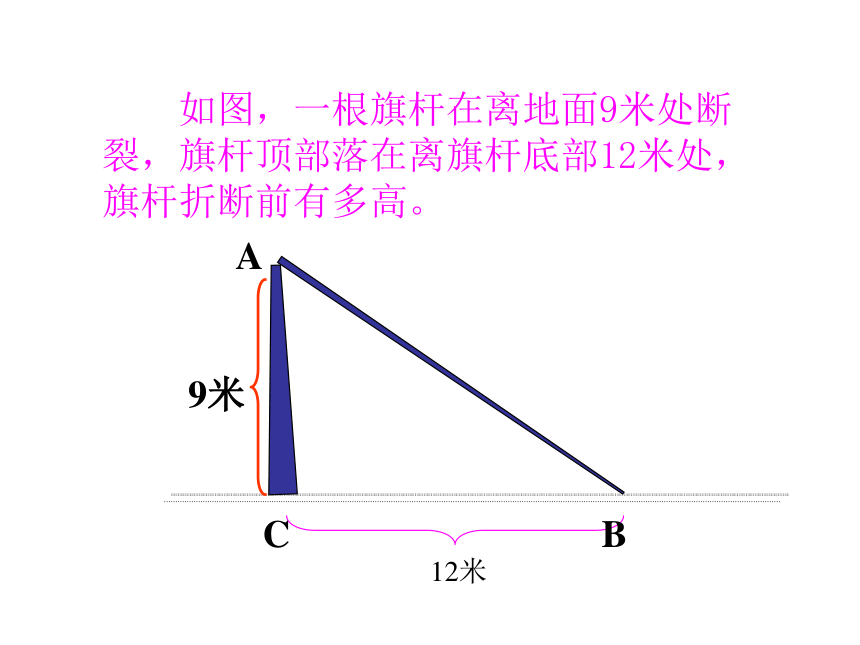
课件21张PPT。课堂因你而精彩 我的课堂我做主 如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
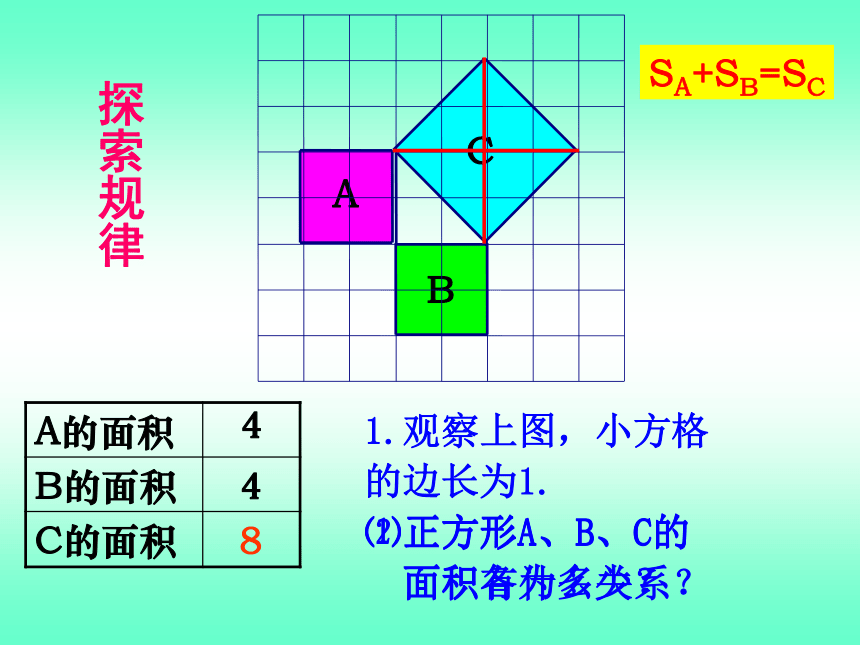
ACB2002年在北京召开的国际数学家大会的会徽勾股定理学习目标:1.经历探索勾股定理的过程,了解勾股定理的由来.2.理解并能用不同的方法证明勾股定理,并能简单的运用.3.提高推理意识与探究习惯,感受我国古代数学的伟大成就.448SA+SB=SC1.观察上图,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
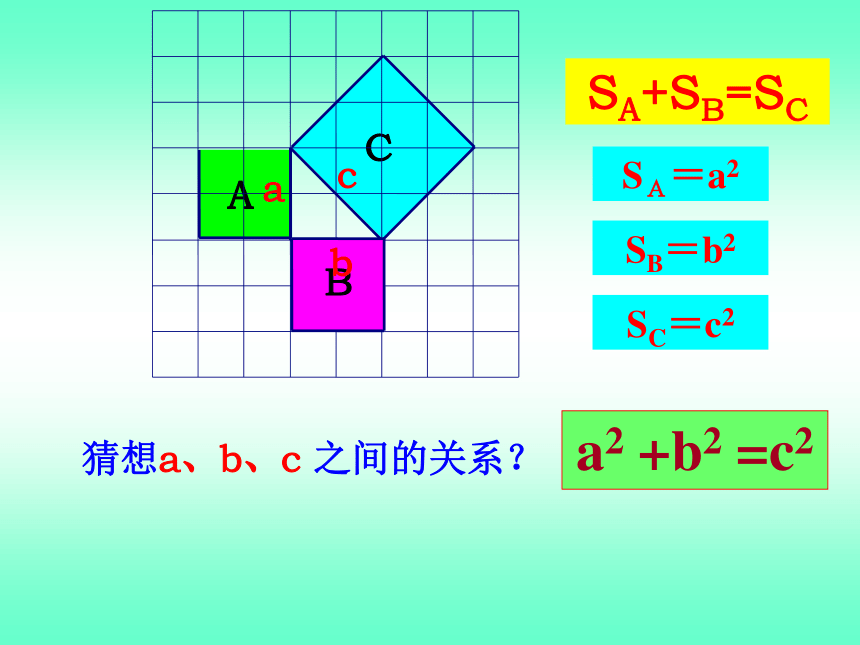
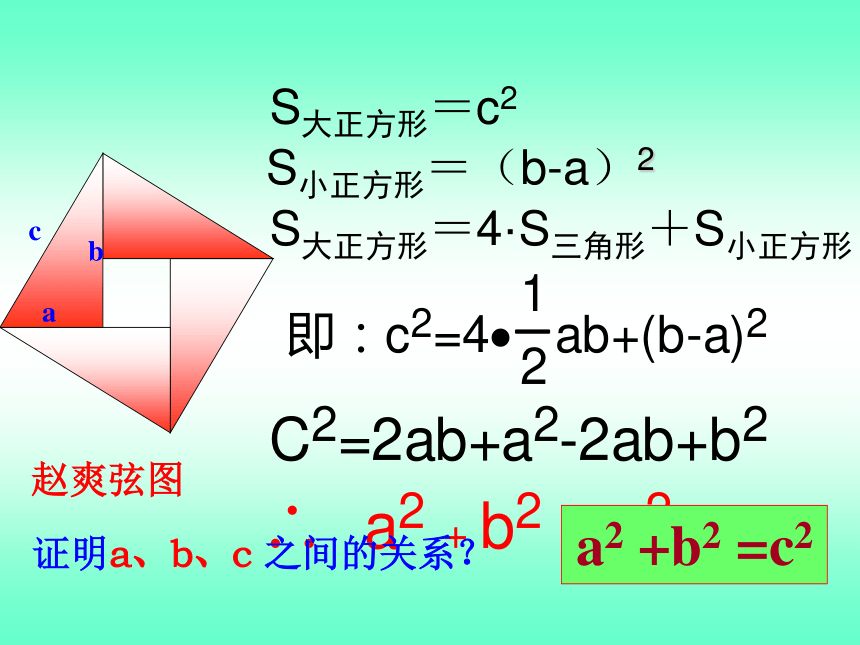
面积有什么关系?探索规律SA+SB=SCabc猜想a、b、c 之间的关系?a2 +b2 =c2SA=a2SB=b2SC=c2abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形赵爽弦图拼图活动一:用四个形状和大小完全相同的直角三角形与一个以直角三角形斜边为边长的正方形拼成一个更大的正方形,然后探究这个正方形的面积。∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab =c2+2ab∴a2 +b2 =c2a2+b2+2abc2+2abaaaabbbbcccc拼图活动二:用两个边长分别为a,b的正方形与四个形状和大小完全相同的直角三角形(与拼图活动一中的四个三角形完全相同)拼成一个大的正方形,并与一中大正方形的面积作比较。aaabbabbac2a2b2a2+b2=c2勾股定理(毕达哥拉斯定理) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股数 学 史 料 在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” ,传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” . 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理” 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2 + b2 =c2a2=c2-b2b2 =c2-a2c2=a2 + b2 例1 在Rt△ABC中,∠C=90°
(1) 已知:a=6,b=8,求c;
(2) 已知:c=13,b=5,求a;
(3) 已知: a:b=3:4,c=15,求a、b.例题分析解:由勾股定理得: c2=a2+b2
=62+82
=100
∴c=10
解:由勾股定理得:
a2=c2-b2
=132-52
=144
∴a=12
解:设a=3k b=4k
由勾股定理得: c2=a2+b2
=9k2+16k2
=25k2
∴c=5k
又∵c=15 ∴k=3
∴a=9 b=12解:根据勾股定理得:
AB2 = AC2 + BC2
= 92 + 122
=81+144
=225
即:AB=15
∴AC+AB=9+15=24(米)
答:旗杆折断前有24米。例2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
ABC5 或 1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .试一试:(合作探究)DA2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形1、本节课我们经历了怎样的学习过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。4、学了本节课后你还有什么困惑?课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。敬请指导再 见
ACB2002年在北京召开的国际数学家大会的会徽勾股定理学习目标:1.经历探索勾股定理的过程,了解勾股定理的由来.2.理解并能用不同的方法证明勾股定理,并能简单的运用.3.提高推理意识与探究习惯,感受我国古代数学的伟大成就.448SA+SB=SC1.观察上图,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
面积有什么关系?探索规律SA+SB=SCabc猜想a、b、c 之间的关系?a2 +b2 =c2SA=a2SB=b2SC=c2abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形赵爽弦图拼图活动一:用四个形状和大小完全相同的直角三角形与一个以直角三角形斜边为边长的正方形拼成一个更大的正方形,然后探究这个正方形的面积。∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab =c2+2ab∴a2 +b2 =c2a2+b2+2abc2+2abaaaabbbbcccc拼图活动二:用两个边长分别为a,b的正方形与四个形状和大小完全相同的直角三角形(与拼图活动一中的四个三角形完全相同)拼成一个大的正方形,并与一中大正方形的面积作比较。aaabbabbac2a2b2a2+b2=c2勾股定理(毕达哥拉斯定理) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股数 学 史 料 在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” ,传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” . 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理” 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2 + b2 =c2a2=c2-b2b2 =c2-a2c2=a2 + b2 例1 在Rt△ABC中,∠C=90°
(1) 已知:a=6,b=8,求c;
(2) 已知:c=13,b=5,求a;
(3) 已知: a:b=3:4,c=15,求a、b.例题分析解:由勾股定理得: c2=a2+b2
=62+82
=100
∴c=10
解:由勾股定理得:
a2=c2-b2
=132-52
=144
∴a=12
解:设a=3k b=4k
由勾股定理得: c2=a2+b2
=9k2+16k2
=25k2
∴c=5k
又∵c=15 ∴k=3
∴a=9 b=12解:根据勾股定理得:
AB2 = AC2 + BC2
= 92 + 122
=81+144
=225
即:AB=15
∴AC+AB=9+15=24(米)
答:旗杆折断前有24米。例2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
ABC5 或 1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .试一试:(合作探究)DA2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形1、本节课我们经历了怎样的学习过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。4、学了本节课后你还有什么困惑?课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。敬请指导再 见
