23.1图形的旋转 课件
文档属性
| 名称 | 23.1图形的旋转 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 406.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-26 11:11:12 | ||
图片预览




文档简介
课件23张PPT。复习回顾1、前面学习过哪些图形的变换?平移变换中对应点所连线段平行(或共线)且相等3、这些图形的变换有什么共同特征?都是全等变换2、这些图形的变换中对应点所连线段有什么
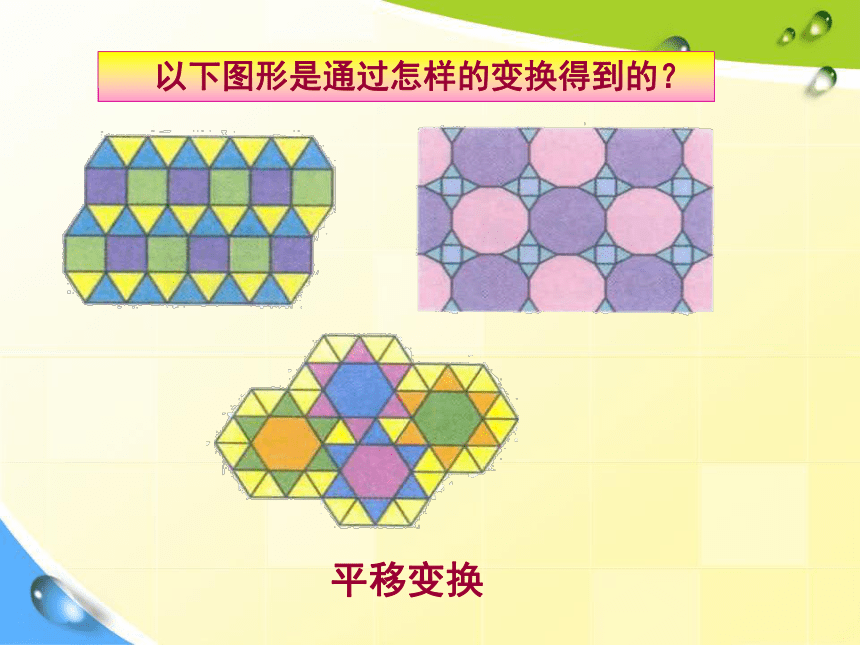
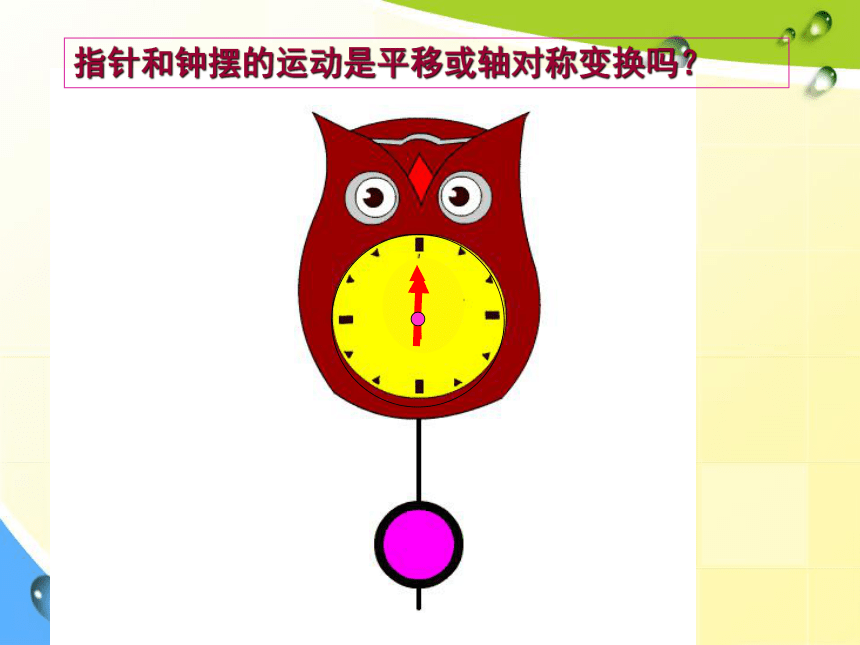
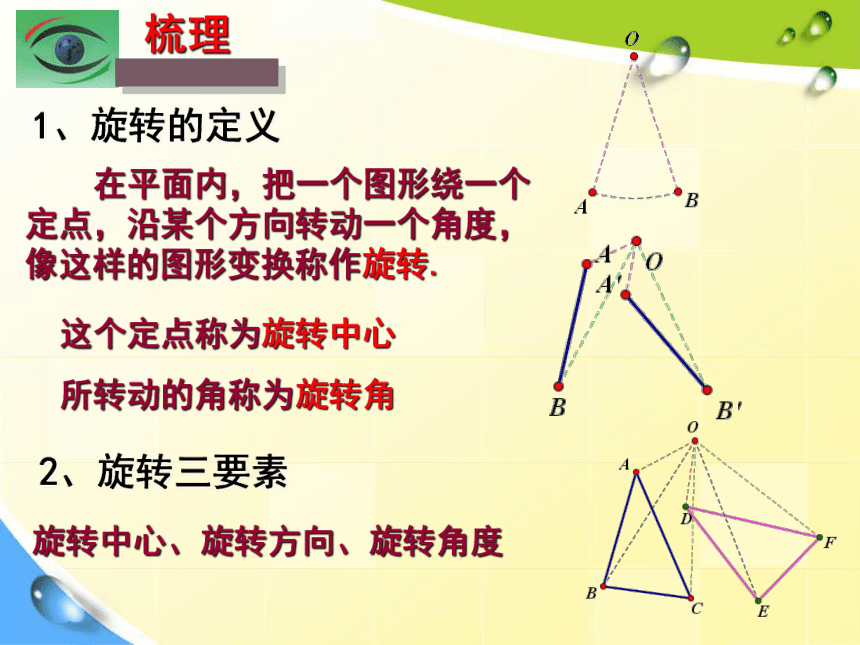
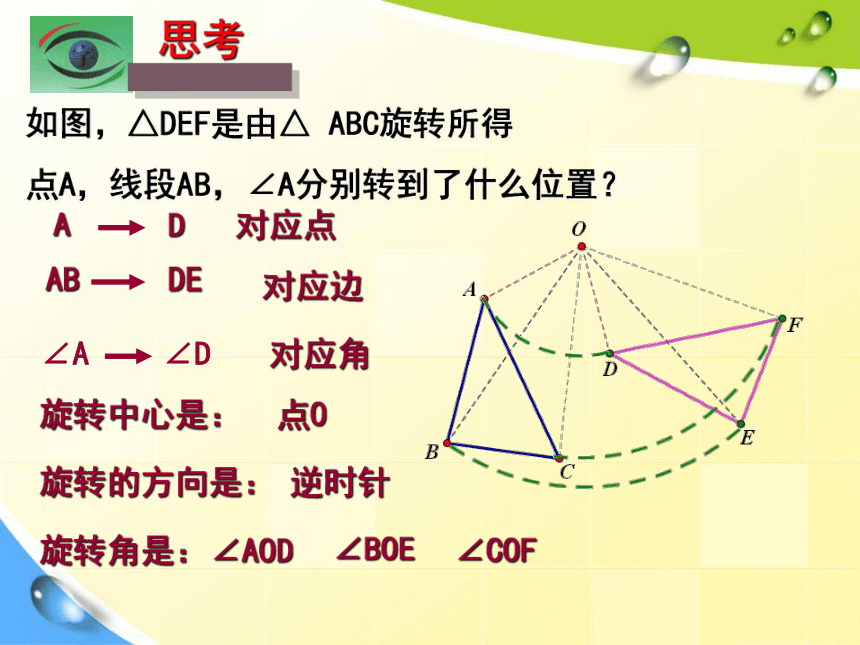
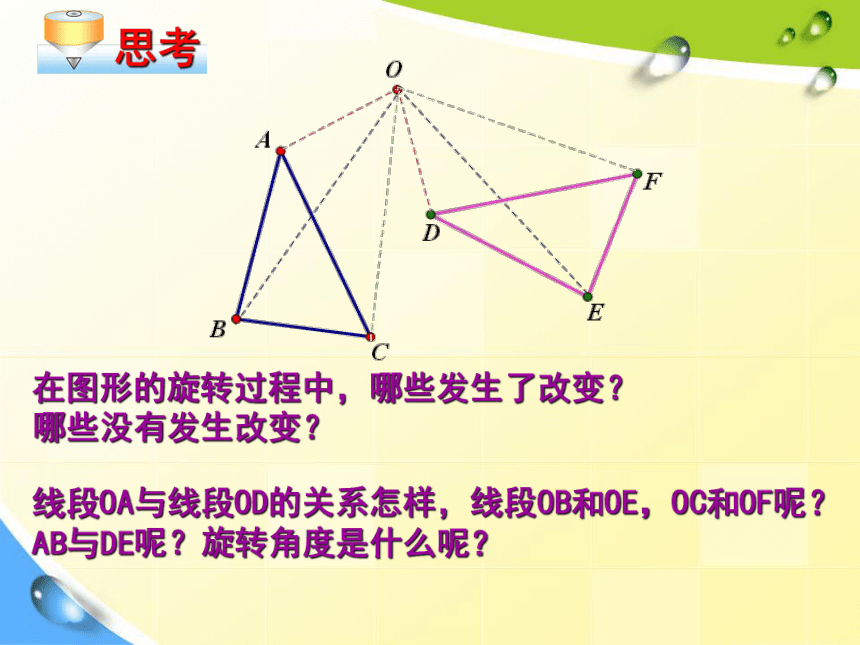
特征?平移变换、轴对称变换轴对称变换中对应点所连线段平行(或共线),且被对称轴垂直平分 以下图形是通过怎样的变换得到的?轴对称变换平移变换 以下图形是通过怎样的变换得到的?指针和钟摆的运动是平移或轴对称变换吗? 这些运动是平移或轴对称变换吗?以上运动有什么共同特征?风车扇叶车轮第二十三章 旋转23.1图形的旋转 在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.这个定点称为旋转中心所转动的角称为旋转角1、旋转的定义2、旋转三要素旋转中心、旋转方向、旋转角度如图,△DEF是由△ ABC旋转所得点A,线段AB,∠A分别转到了什么位置?DDE∠D对应点对应边对应角旋转中心是:旋转的方向是:旋转角是:点O逆时针在图形的旋转过程中,哪些发生了改变?
哪些没有发生改变? 线段OA与线段OD的关系怎样,线段OB和OE,OC和OF呢?
AB与DE呢?旋转角度是什么呢?思考①旋转前后的图形全等 ②对应点到旋转中心的距离相等 ③对应点与旋转中心所连线段的夹角
等于旋转角 3、旋转的基本性质四边形ABCD是边长为1的正方形,且DE= ,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?点A (2)∵ △ABF是由△ADE旋转而得的,
∴ B是D的对应点。
∴ ∠DAB是旋转角,而∠DAB = 90°,即旋转了90°。例题讲解(3)∵AD=1,DE=
∴
∵ AF 是AE 的对应边
∴ AF = AE =? (3)AF的长度是多少? (4)如果连结EF,那么△AEF是怎样的三角形?(1)地下水位下降;(2)传送带的移动;
(3)方向盘的转动;(4)水龙头开关的转动;
(5)钟摆的运动; (6)荡秋千运动;
(7)摩托车在急刹车时向前滑动;
(8)飞机起飞后冲向空中的过程;
(9)转盘的转动;
(10)笔直的铁轨上飞驰而过的火车。1、下列现象中属于旋转的有( )个 A、4 B、5 C、6 D、7B练习2、△A′OB′是由△AOB绕点O逆时针旋转
得到的,已知∠AOB=20°,∠A′OB=30°,
AB=3,OB=7,则A′B′= ,
OB′= ,∠A′OB′= °,
旋转角= °。372050练习3、如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及∠CAE、∠E、∠BAE的度数。4、如图,将矩形ABCD绕点A顺时针旋转90゜后,得到矩形AB′C ′D′,如果CD=2DA=2,那么CC′=_________. 简单的旋转作图AO例1 将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限特殊角)作出∠AOB,与圆周交于B点;
3.B点即为所求作.B点的旋转作法 简单的旋转作图AO例2 将线段AB绕O点沿顺时针方向旋转60?.作法:
1、将点A绕点O顺时针旋转
60?,得点C;
2、将点B绕点O顺时针旋转
60 ?,得点D ;
3、连接CD, 则线段CD即为
所求作.CBD线段的旋转作法简单的旋转作图例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得
∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE图形的旋转作法ABCDEF如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心。 旋转中心在对应点所连
线段的垂直平分线上。O如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O经典习题解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.回 顾本节课你学到了什么?你还有什么困惑?旋转的定义旋转三要素旋转的性质
特征?平移变换、轴对称变换轴对称变换中对应点所连线段平行(或共线),且被对称轴垂直平分 以下图形是通过怎样的变换得到的?轴对称变换平移变换 以下图形是通过怎样的变换得到的?指针和钟摆的运动是平移或轴对称变换吗? 这些运动是平移或轴对称变换吗?以上运动有什么共同特征?风车扇叶车轮第二十三章 旋转23.1图形的旋转 在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.这个定点称为旋转中心所转动的角称为旋转角1、旋转的定义2、旋转三要素旋转中心、旋转方向、旋转角度如图,△DEF是由△ ABC旋转所得点A,线段AB,∠A分别转到了什么位置?DDE∠D对应点对应边对应角旋转中心是:旋转的方向是:旋转角是:点O逆时针在图形的旋转过程中,哪些发生了改变?
哪些没有发生改变? 线段OA与线段OD的关系怎样,线段OB和OE,OC和OF呢?
AB与DE呢?旋转角度是什么呢?思考①旋转前后的图形全等 ②对应点到旋转中心的距离相等 ③对应点与旋转中心所连线段的夹角
等于旋转角 3、旋转的基本性质四边形ABCD是边长为1的正方形,且DE= ,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?点A (2)∵ △ABF是由△ADE旋转而得的,
∴ B是D的对应点。
∴ ∠DAB是旋转角,而∠DAB = 90°,即旋转了90°。例题讲解(3)∵AD=1,DE=
∴
∵ AF 是AE 的对应边
∴ AF = AE =? (3)AF的长度是多少? (4)如果连结EF,那么△AEF是怎样的三角形?(1)地下水位下降;(2)传送带的移动;
(3)方向盘的转动;(4)水龙头开关的转动;
(5)钟摆的运动; (6)荡秋千运动;
(7)摩托车在急刹车时向前滑动;
(8)飞机起飞后冲向空中的过程;
(9)转盘的转动;
(10)笔直的铁轨上飞驰而过的火车。1、下列现象中属于旋转的有( )个 A、4 B、5 C、6 D、7B练习2、△A′OB′是由△AOB绕点O逆时针旋转
得到的,已知∠AOB=20°,∠A′OB=30°,
AB=3,OB=7,则A′B′= ,
OB′= ,∠A′OB′= °,
旋转角= °。372050练习3、如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及∠CAE、∠E、∠BAE的度数。4、如图,将矩形ABCD绕点A顺时针旋转90゜后,得到矩形AB′C ′D′,如果CD=2DA=2,那么CC′=_________. 简单的旋转作图AO例1 将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限特殊角)作出∠AOB,与圆周交于B点;
3.B点即为所求作.B点的旋转作法 简单的旋转作图AO例2 将线段AB绕O点沿顺时针方向旋转60?.作法:
1、将点A绕点O顺时针旋转
60?,得点C;
2、将点B绕点O顺时针旋转
60 ?,得点D ;
3、连接CD, 则线段CD即为
所求作.CBD线段的旋转作法简单的旋转作图例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得
∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE图形的旋转作法ABCDEF如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心。 旋转中心在对应点所连
线段的垂直平分线上。O如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O经典习题解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.回 顾本节课你学到了什么?你还有什么困惑?旋转的定义旋转三要素旋转的性质
同课章节目录
