湘教版八年级数学下册 2.5.2矩形的判定 教学设计
文档属性
| 名称 | 湘教版八年级数学下册 2.5.2矩形的判定 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览

文档简介
矩形的判定
一、教学目标及重难点
教学目标:
1、知识与技能:探索并证明矩形的判定定理,会运用矩形的判定定理判定一个四边形是矩形。
2、过程与方法:
本节课以平行四边形定义为基础,通过问题的提出,运用剪一剪、议一议、判一判及师生共同探索启发等方式得出矩形的三个判定方法并在运用中巩固所学知识。
3、情感态度与价值观:
在学习过程中,培养学生自主探索的能力,培养学生数学的学习兴趣,体会数学的思考方法。
4、教学重点:矩形判定定理的探索证明与运用
5、教学难点:矩形判定方法的理解与选择运用
二、教学过程:
(一)复习旧知、导入新课
1、矩形的定义是怎样的?
矩形的定义:有一个角是直角的平行四边形叫作矩形。
(课件展示定义的实质)
(二)、创设问题、酝酿新知
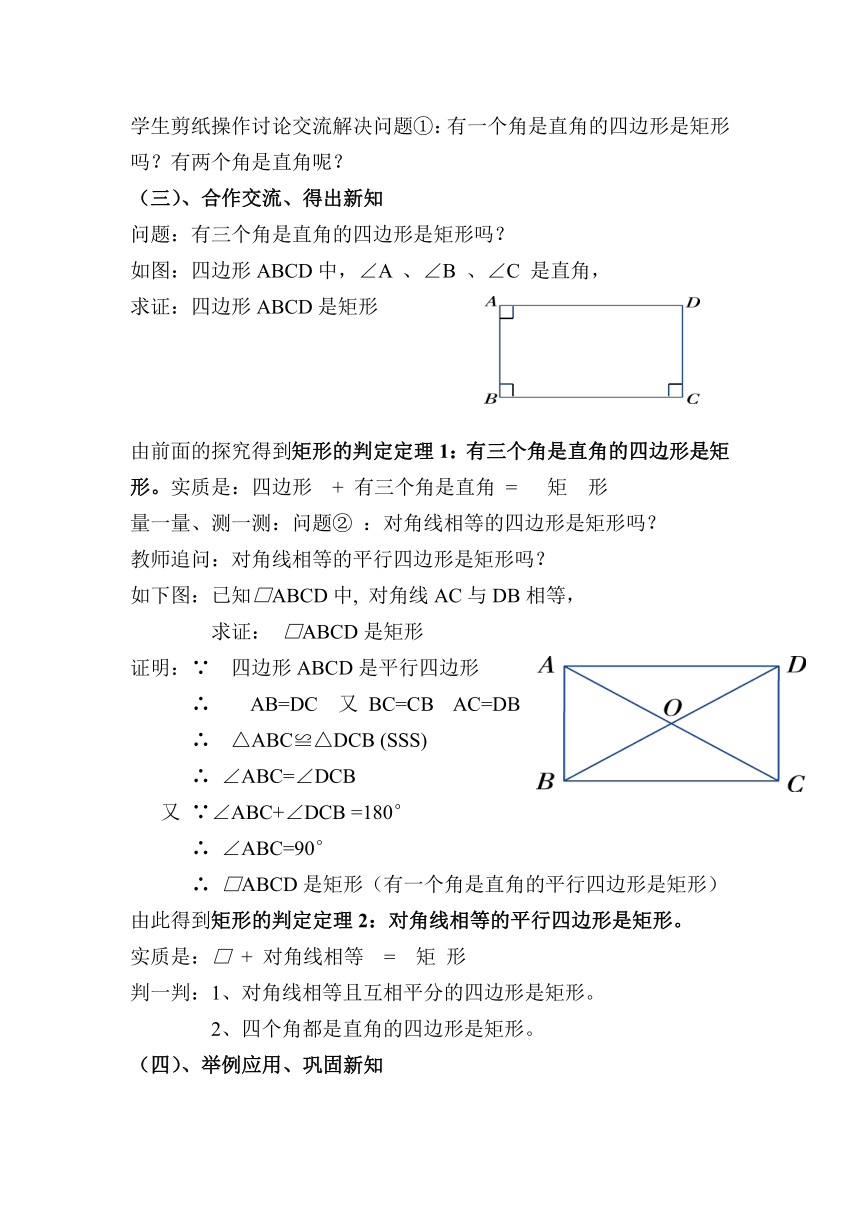
正在上八年级的小聪,是个爱学习的孩子!他喜欢思考问题。学完矩形的性质一课后,数学老师布置以下三个问题要求同学们课外思考:①有一个角是直角的四边形是矩形吗?有两个角是直角呢?有三个角是直角的四边形呢?四个角都是直角的四边形呢?②对角线相等的四边形是矩形吗?
③对角线相等的平行四边形是矩形吗?
学生剪纸操作讨论交流解决问题①:有一个角是直角的四边形是矩形吗?有两个角是直角呢?
(三)、合作交流、得出新知
问题:有三个角是直角的四边形是矩形吗?
如图:四边形ABCD中,∠A 、∠B 、∠C 是直角,
求证:四边形ABCD是矩形
由前面的探究得到矩形的判定定理1:有三个角是直角的四边形是矩形。实质是:四边形 + 有三个角是直角 = 矩 形
量一量、测一测:问题② :对角线相等的四边形是矩形吗?
教师追问:对角线相等的平行四边形是矩形吗?
如下图:已知□ABCD中, 对角线AC与DB相等,
求证: □ABCD是矩形
证明:∵ 四边形ABCD是平行四边形
∴ AB=DC 又 BC=CB AC=DB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
又 ∵∠ABC+∠DCB =180°
∴ ∠ABC=90°
∴ □ABCD是矩形(有一个角是直角的平行四边形是矩形)
由此得到矩形的判定定理2:对角线相等的平行四边形是矩形。
实质是:□ + 对角线相等 = 矩 形
判一判:1、对角线相等且互相平分的四边形是矩形。
2、四个角都是直角的四边形是矩形。
(四)、举例应用、巩固新知
例题1:(2015湖南中考)如图,在□ABCD中,DE⊥AB , BF⊥CD, 垂足分别为E、F,求证:四边形BFDE是矩形。
例题2:如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,连接EF、FG、GH、HE,求证:四边形EFGH是矩形
(五)、巩固练习、升华新知
练习题: 如图,在□ABCD中,对角线AC,BD相交于点O,
∠AOB = 60°,AB= 2,AC= 4,求证:□ABCD是矩形
(六)、课堂小结、收获新知
1、矩形的判定方法有哪些?
①矩形的定义:有一个角是直角的平行四边形叫作矩形。
②矩形的判定定理1:对角线相等的平行四边形是矩形。
③矩形的判定定理2:有三个角是直角的四边形是矩形
2、运用矩形的三个判定方法时要注意什么问题?
(1)注意三个判定方法的应用基础条件:
①②是要求以平行四边形为基础,③是以四边形为基础,直接证明四边形是矩形。
(2)根据已知条件,选择恰当的判定方法
(七)、布置作业、深化新知:
1、数学课本:64页6、7两题。
2、学习寄语:
——学习没有捷径,唯有刻苦与努力,并长期坚持!
——所谓的天才,就是99﹪汗水+ 1 ﹪的灵感。
三、板书设计:
矩形的判定
矩形的判定方法:
1、矩形的定义:有一个角是直角的平行四边形是矩形
2、矩形的判定定理1:有三个角是直角的四边形是矩形。
3、矩形的判定定理2:对角线相等的平行四边形是矩形
(或对角线相等且互相平分的四边形是矩形)
例题1:教师点拨、学生上台板演证明过程
例题2:师生共析,学生思考后口述,教师在多媒体上展示
习题: 自主完成,学生代表口述,教师在多媒体订正
E
F
O
E
F
G
H
一、教学目标及重难点
教学目标:
1、知识与技能:探索并证明矩形的判定定理,会运用矩形的判定定理判定一个四边形是矩形。
2、过程与方法:
本节课以平行四边形定义为基础,通过问题的提出,运用剪一剪、议一议、判一判及师生共同探索启发等方式得出矩形的三个判定方法并在运用中巩固所学知识。
3、情感态度与价值观:
在学习过程中,培养学生自主探索的能力,培养学生数学的学习兴趣,体会数学的思考方法。
4、教学重点:矩形判定定理的探索证明与运用
5、教学难点:矩形判定方法的理解与选择运用
二、教学过程:
(一)复习旧知、导入新课
1、矩形的定义是怎样的?
矩形的定义:有一个角是直角的平行四边形叫作矩形。
(课件展示定义的实质)
(二)、创设问题、酝酿新知
正在上八年级的小聪,是个爱学习的孩子!他喜欢思考问题。学完矩形的性质一课后,数学老师布置以下三个问题要求同学们课外思考:①有一个角是直角的四边形是矩形吗?有两个角是直角呢?有三个角是直角的四边形呢?四个角都是直角的四边形呢?②对角线相等的四边形是矩形吗?
③对角线相等的平行四边形是矩形吗?
学生剪纸操作讨论交流解决问题①:有一个角是直角的四边形是矩形吗?有两个角是直角呢?
(三)、合作交流、得出新知
问题:有三个角是直角的四边形是矩形吗?
如图:四边形ABCD中,∠A 、∠B 、∠C 是直角,
求证:四边形ABCD是矩形
由前面的探究得到矩形的判定定理1:有三个角是直角的四边形是矩形。实质是:四边形 + 有三个角是直角 = 矩 形
量一量、测一测:问题② :对角线相等的四边形是矩形吗?
教师追问:对角线相等的平行四边形是矩形吗?
如下图:已知□ABCD中, 对角线AC与DB相等,
求证: □ABCD是矩形
证明:∵ 四边形ABCD是平行四边形
∴ AB=DC 又 BC=CB AC=DB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
又 ∵∠ABC+∠DCB =180°
∴ ∠ABC=90°
∴ □ABCD是矩形(有一个角是直角的平行四边形是矩形)
由此得到矩形的判定定理2:对角线相等的平行四边形是矩形。
实质是:□ + 对角线相等 = 矩 形
判一判:1、对角线相等且互相平分的四边形是矩形。
2、四个角都是直角的四边形是矩形。
(四)、举例应用、巩固新知
例题1:(2015湖南中考)如图,在□ABCD中,DE⊥AB , BF⊥CD, 垂足分别为E、F,求证:四边形BFDE是矩形。
例题2:如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,连接EF、FG、GH、HE,求证:四边形EFGH是矩形
(五)、巩固练习、升华新知
练习题: 如图,在□ABCD中,对角线AC,BD相交于点O,
∠AOB = 60°,AB= 2,AC= 4,求证:□ABCD是矩形
(六)、课堂小结、收获新知
1、矩形的判定方法有哪些?
①矩形的定义:有一个角是直角的平行四边形叫作矩形。
②矩形的判定定理1:对角线相等的平行四边形是矩形。
③矩形的判定定理2:有三个角是直角的四边形是矩形
2、运用矩形的三个判定方法时要注意什么问题?
(1)注意三个判定方法的应用基础条件:
①②是要求以平行四边形为基础,③是以四边形为基础,直接证明四边形是矩形。
(2)根据已知条件,选择恰当的判定方法
(七)、布置作业、深化新知:
1、数学课本:64页6、7两题。
2、学习寄语:
——学习没有捷径,唯有刻苦与努力,并长期坚持!
——所谓的天才,就是99﹪汗水+ 1 ﹪的灵感。
三、板书设计:
矩形的判定
矩形的判定方法:
1、矩形的定义:有一个角是直角的平行四边形是矩形
2、矩形的判定定理1:有三个角是直角的四边形是矩形。
3、矩形的判定定理2:对角线相等的平行四边形是矩形
(或对角线相等且互相平分的四边形是矩形)
例题1:教师点拨、学生上台板演证明过程
例题2:师生共析,学生思考后口述,教师在多媒体上展示
习题: 自主完成,学生代表口述,教师在多媒体订正
E
F
O
E
F
G
H
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
