湘教版八年级数学下册 2.5.1矩形的性质 教学设计
文档属性
| 名称 | 湘教版八年级数学下册 2.5.1矩形的性质 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 434.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览

文档简介
2.5.1矩形的性质
教学目标
1、掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系;
2、会初步运用矩形的概念和性质来解决有关问题。
3、经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思维方法。并 渗透运动联系、从量变到质变的观点。
4、培养严谨的推理能力,以及自主合的精神,体会逻辑推理的思维价值。
重点:矩形的性质
难点:矩形的性质的灵活应用
教学过程:
一、
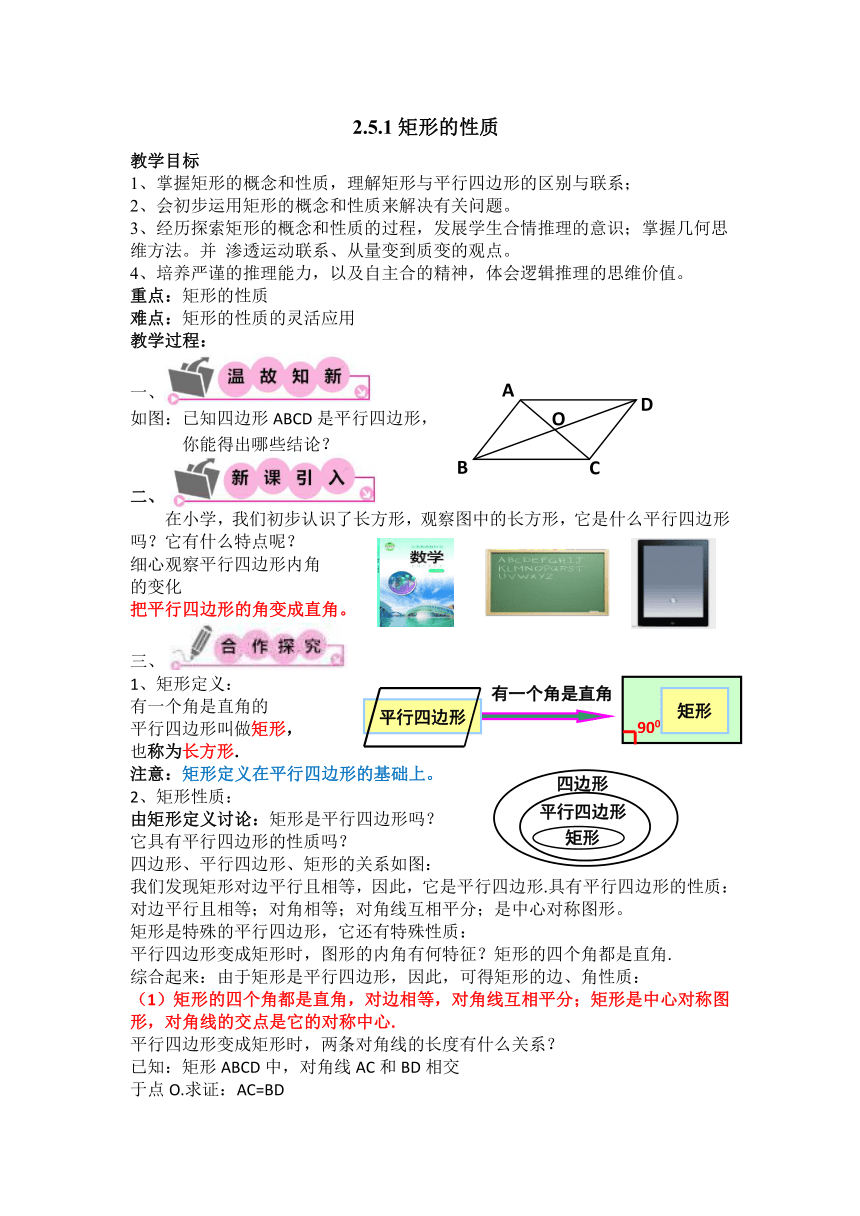
如图:已知四边形ABCD是平行四边形,
你能得出哪些结论?
二、
在小学,我们初步认识了长方形,观察图中的长方形,它是什么平行四边形吗?它有什么特点呢?
细心观察平行四边形内角
的变化
把平行四边形的角变成直角。
1、矩形定义:
有一个角是直角的
平行四边形叫做矩形,
也称为长方形.
注意:矩形定义在平行四边形的基础上。
2、矩形性质:
由矩形定义讨论:矩形是平行四边形吗?
它具有平行四边形的性质吗?
四边形、平行四边形、矩形的关系如图:
我们发现矩形对边平行且相等,因此,它是平行四边形.具有平行四边形的性质:
对边平行且相等;对角相等;对角线互相平分;是中心对称图形。
矩形是特殊的平行四边形,它还有特殊性质:
平行四边形变成矩形时,图形的内角有何特征?矩形的四个角都是直角.
综合起来:由于矩形是平行四边形,因此,可得矩形的边、角性质:
(1)矩形的四个角都是直角,对边相等,对角线互相平分;矩形是中心对称图形,对角线的交点是它的对称中心.
平行四边形变成矩形时,两条对角线的长度有什么关系?
已知:矩形ABCD中,对角线AC和BD相交
于点O.求证:AC=BD
证明一:∵四边形ABCD是矩形,∴AB=CD,
∠ABC=∠DCB,∴△ABC≌△DCB ,∴AC=BD
证明二:∵四边形ABCD是矩形,
∴ ∠ABC=∠DCB=90°, AB=CD
∴ AC2=BC2+AB2 BD2=BC2+CD2
∴AC=BD
(2)由此得到矩形对角线的性质:矩形的对角线相等.
(3)如图,矩形的对称性:
拿出一张矩形纸,怎样折叠能使
矩形在折痕两旁的部分互相重合?
满足这个要求的折叠方法有几种?
矩形又是轴对称图形,过每一组对
边中点的直线都是矩形的对称轴.
四、
例 如图,矩形ABCD的两条对角线AC ,BD相交于点O,
AC = 4 cm, ∠AOB = 60°. 求BC的长.
解:∵ □ABCD是矩形,
∴OA=OB=AC=2cm,又∠AOB = 60°,
∴ △AOB是等边三角形. ∴ AB=OA=2cm.
∵ ∠ABC = 90°,∴ 在Rt△ABC中,
五、
通过这节课的学习,你有什么收获?
有一个角是直角的平行四边形叫做矩形,也称为长方形.
注意:矩形定义在平行四边形的基础上
矩形的性质:四个角都是直角,对边平行且相等,对角线互相平分
矩形的对角线相等
课 堂 测 评
1.矩形具有而一般平行四边形不具有的性质是( )
A、对角线相等 B、对边相等 C、对角相等 D、对角线互相平分
2.已知: 如图,矩形ABCD的两条对角线交于点O, AB= 4cm ,
∠AOB=60°。则矩形对角线的长为 。
3.如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,则矩形ABCD的周长为 。
教学目标
1、掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系;
2、会初步运用矩形的概念和性质来解决有关问题。
3、经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思维方法。并 渗透运动联系、从量变到质变的观点。
4、培养严谨的推理能力,以及自主合的精神,体会逻辑推理的思维价值。
重点:矩形的性质
难点:矩形的性质的灵活应用
教学过程:
一、
如图:已知四边形ABCD是平行四边形,
你能得出哪些结论?
二、
在小学,我们初步认识了长方形,观察图中的长方形,它是什么平行四边形吗?它有什么特点呢?
细心观察平行四边形内角
的变化
把平行四边形的角变成直角。
1、矩形定义:
有一个角是直角的
平行四边形叫做矩形,
也称为长方形.
注意:矩形定义在平行四边形的基础上。
2、矩形性质:
由矩形定义讨论:矩形是平行四边形吗?
它具有平行四边形的性质吗?
四边形、平行四边形、矩形的关系如图:
我们发现矩形对边平行且相等,因此,它是平行四边形.具有平行四边形的性质:
对边平行且相等;对角相等;对角线互相平分;是中心对称图形。
矩形是特殊的平行四边形,它还有特殊性质:
平行四边形变成矩形时,图形的内角有何特征?矩形的四个角都是直角.
综合起来:由于矩形是平行四边形,因此,可得矩形的边、角性质:
(1)矩形的四个角都是直角,对边相等,对角线互相平分;矩形是中心对称图形,对角线的交点是它的对称中心.
平行四边形变成矩形时,两条对角线的长度有什么关系?
已知:矩形ABCD中,对角线AC和BD相交
于点O.求证:AC=BD
证明一:∵四边形ABCD是矩形,∴AB=CD,
∠ABC=∠DCB,∴△ABC≌△DCB ,∴AC=BD
证明二:∵四边形ABCD是矩形,
∴ ∠ABC=∠DCB=90°, AB=CD
∴ AC2=BC2+AB2 BD2=BC2+CD2
∴AC=BD
(2)由此得到矩形对角线的性质:矩形的对角线相等.
(3)如图,矩形的对称性:
拿出一张矩形纸,怎样折叠能使
矩形在折痕两旁的部分互相重合?
满足这个要求的折叠方法有几种?
矩形又是轴对称图形,过每一组对
边中点的直线都是矩形的对称轴.
四、
例 如图,矩形ABCD的两条对角线AC ,BD相交于点O,
AC = 4 cm, ∠AOB = 60°. 求BC的长.
解:∵ □ABCD是矩形,
∴OA=OB=AC=2cm,又∠AOB = 60°,
∴ △AOB是等边三角形. ∴ AB=OA=2cm.
∵ ∠ABC = 90°,∴ 在Rt△ABC中,
五、
通过这节课的学习,你有什么收获?
有一个角是直角的平行四边形叫做矩形,也称为长方形.
注意:矩形定义在平行四边形的基础上
矩形的性质:四个角都是直角,对边平行且相等,对角线互相平分
矩形的对角线相等
课 堂 测 评
1.矩形具有而一般平行四边形不具有的性质是( )
A、对角线相等 B、对边相等 C、对角相等 D、对角线互相平分
2.已知: 如图,矩形ABCD的两条对角线交于点O, AB= 4cm ,
∠AOB=60°。则矩形对角线的长为 。
3.如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,则矩形ABCD的周长为 。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
