苏科版七年级数学下册《7.2 探索平行线的性质——判定、性质的综合运用》教学设计
文档属性
| 名称 | 苏科版七年级数学下册《7.2 探索平行线的性质——判定、性质的综合运用》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 106.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-20 00:00:00 | ||
图片预览

文档简介
7.2 探索平行线的性质(2)
——判定、性质的综合运用
【教学目标】
1、会证明直线平行的条件和平行线的性质,认识平行作为两条直线的位置关系与角的大小存在着内在联系。
2、掌握相关图形语言、文字语言、符号语言及其互换。
3、在观察——实验——猜想——证明的过程中体验探索的方法,逐步形成严谨的思维品质。
【教学重点】
直线平行的条件和平行线性质的运用。
【教学难点】
平行线的性质与判定的区别与联系。
【教学过程】
一、复习提问:
(1)判定两直线平行的方法有哪些?怎样用符号语言表述?
(2)若两直线平行,那么同位角有什么关系呢?内错角和同旁内角呢?
【设计目的】引导学生明确判定与性质最大的区别在于条件和结论互逆.这里是学生升入初中以来第一次接触判定和性质,要让学生明确它们之间的区别,防止在应用时发生混淆.为后面学习其他图形的判定和性质作好铺垫.
牛刀小试:
1、填空。
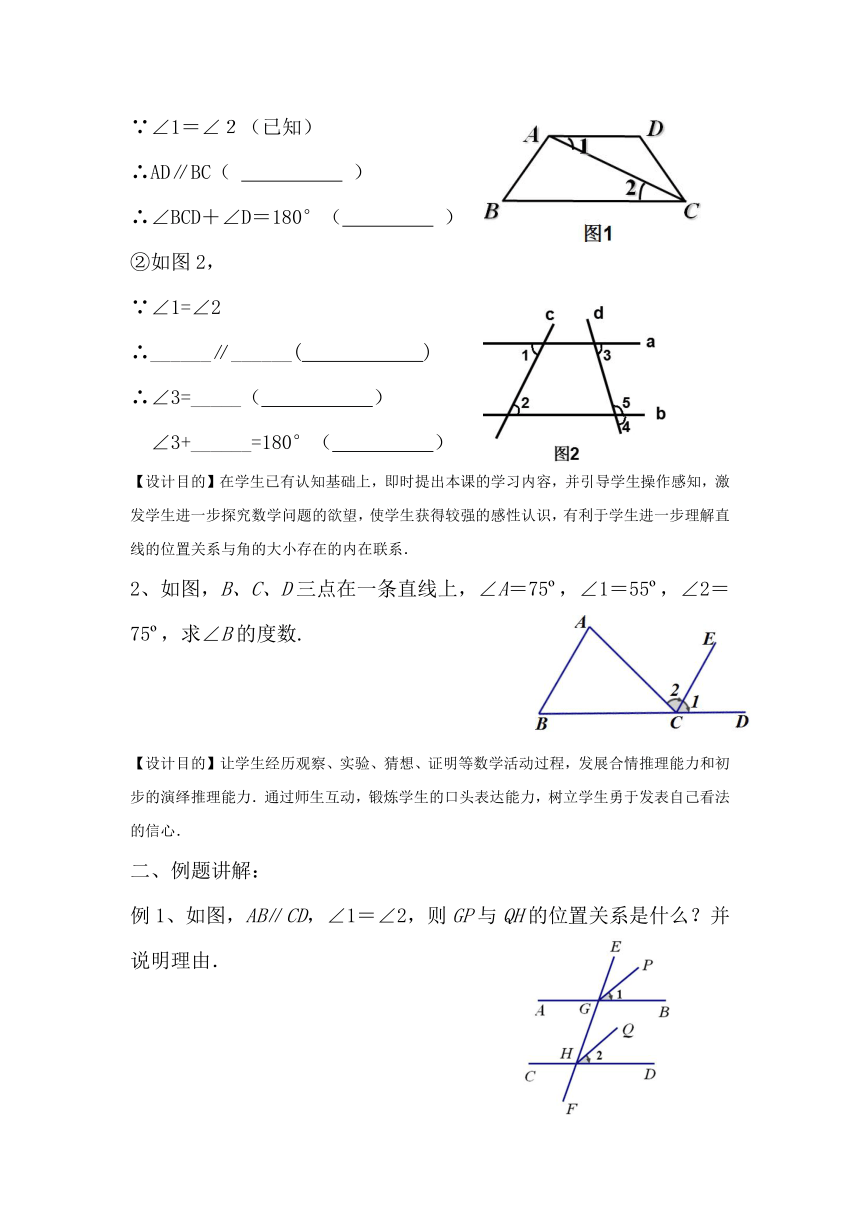
①如图1:
∵∠1=∠2(已知)
∴AD∥BC( )
∴∠BCD+∠D=180°( )
②如图2,
∵∠1=∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=180°( )
【设计目的】在学生已有认知基础上,即时提出本课的学习内容,并引导学生操作感知,激发学生进一步探究数学问题的欲望,使学生获得较强的感性认识,有利于学生进一步理解直线的位置关系与角的大小存在的内在联系.
2、如图,B、C、D三点在一条直线上,∠A=75 ,∠1=55 ,∠2=75 ,求∠B的度数.
【设计目的】让学生经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力.通过师生互动,锻炼学生的口头表达能力,树立学生勇于发表自己看法的信心.
二、例题讲解:
例1、如图,AB∥CD,∠1=∠2,则GP与QH的位置关系是什么?并说明理由.
【设计目的】引导学生认识平行作为两条直线的位置关系,与角的大小存在着内在联系:由角的数量关系判定直线的位置关系;由直线的位置关系决定角的数量关系。
例2、如图,AD∥BC,∠A=∠C.试说明AB∥CD.
【设计目的】在解题过程中辨析判定和性质,进一步明确判定和性质的区别.从简单图形到复杂图形、从单一知识到几个知识的综合运用,进一步提高学生的识图能力,逐步提高推理能力和解决问题的能力.
例3、潜望镜中的两个镜子MN和PQ是相互平行的,光线AB经镜面反射时,∠1=∠2,∠3=∠4。进入的光线AB与反射出的光线CD平行吗?为什么?
【设计目的】让学生经历观察、实验、猜想、证明等数学活动过程,发展合情推理和演绎推理能力,能有条理地、清楚地阐明自己的观点。
三、课堂小结:
通过对平行线知识的运用,你有哪些收获和体会?
【设计目的】引导学生从知识和技能两方面进行归纳.帮助学生梳理知识脉络,引导学生说明白性质和判定的联系和区别,提升学生的认识.
条件:角的关系→平行关系.
特征:平行关系→角的关系.
四、作业布置
1、课后作业:
2、拓展提高
例 如图,AB∥CD.试说明∠A+∠E+∠C =360°.
变式:如图,AB∥CD.试说明∠A+∠C=∠E
【设计目的】实现《课程标准》中所要求的“让不同层次的学生得到不同的发展”.
——判定、性质的综合运用
【教学目标】
1、会证明直线平行的条件和平行线的性质,认识平行作为两条直线的位置关系与角的大小存在着内在联系。
2、掌握相关图形语言、文字语言、符号语言及其互换。
3、在观察——实验——猜想——证明的过程中体验探索的方法,逐步形成严谨的思维品质。
【教学重点】
直线平行的条件和平行线性质的运用。
【教学难点】
平行线的性质与判定的区别与联系。
【教学过程】
一、复习提问:
(1)判定两直线平行的方法有哪些?怎样用符号语言表述?
(2)若两直线平行,那么同位角有什么关系呢?内错角和同旁内角呢?
【设计目的】引导学生明确判定与性质最大的区别在于条件和结论互逆.这里是学生升入初中以来第一次接触判定和性质,要让学生明确它们之间的区别,防止在应用时发生混淆.为后面学习其他图形的判定和性质作好铺垫.
牛刀小试:
1、填空。
①如图1:
∵∠1=∠2(已知)
∴AD∥BC( )
∴∠BCD+∠D=180°( )
②如图2,
∵∠1=∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=180°( )
【设计目的】在学生已有认知基础上,即时提出本课的学习内容,并引导学生操作感知,激发学生进一步探究数学问题的欲望,使学生获得较强的感性认识,有利于学生进一步理解直线的位置关系与角的大小存在的内在联系.
2、如图,B、C、D三点在一条直线上,∠A=75 ,∠1=55 ,∠2=75 ,求∠B的度数.
【设计目的】让学生经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力.通过师生互动,锻炼学生的口头表达能力,树立学生勇于发表自己看法的信心.
二、例题讲解:
例1、如图,AB∥CD,∠1=∠2,则GP与QH的位置关系是什么?并说明理由.
【设计目的】引导学生认识平行作为两条直线的位置关系,与角的大小存在着内在联系:由角的数量关系判定直线的位置关系;由直线的位置关系决定角的数量关系。
例2、如图,AD∥BC,∠A=∠C.试说明AB∥CD.
【设计目的】在解题过程中辨析判定和性质,进一步明确判定和性质的区别.从简单图形到复杂图形、从单一知识到几个知识的综合运用,进一步提高学生的识图能力,逐步提高推理能力和解决问题的能力.
例3、潜望镜中的两个镜子MN和PQ是相互平行的,光线AB经镜面反射时,∠1=∠2,∠3=∠4。进入的光线AB与反射出的光线CD平行吗?为什么?
【设计目的】让学生经历观察、实验、猜想、证明等数学活动过程,发展合情推理和演绎推理能力,能有条理地、清楚地阐明自己的观点。
三、课堂小结:
通过对平行线知识的运用,你有哪些收获和体会?
【设计目的】引导学生从知识和技能两方面进行归纳.帮助学生梳理知识脉络,引导学生说明白性质和判定的联系和区别,提升学生的认识.
条件:角的关系→平行关系.
特征:平行关系→角的关系.
四、作业布置
1、课后作业:
2、拓展提高
例 如图,AB∥CD.试说明∠A+∠E+∠C =360°.
变式:如图,AB∥CD.试说明∠A+∠C=∠E
【设计目的】实现《课程标准》中所要求的“让不同层次的学生得到不同的发展”.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
