人教版数学三年级下册 第2单元第2节第5课时《解决问题》教案
文档属性
| 名称 | 人教版数学三年级下册 第2单元第2节第5课时《解决问题》教案 |  | |
| 格式 | docx | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 07:32:59 | ||
图片预览



文档简介
第5课时 解决问题
备教材内容
1.本课时学习的是教材29、30页的内容。
2.例8呈现了一家人住宿宾馆结账的情境,引导学生用估算解决“每天的住宿费的问题”,感受数学与日常生活的密切联系。例9创设了“用18个纸箱装菠萝够不够”的问题情境,并给出不同的解决问题的策略,使学生明确解决同一个问题可以有不同的方法,只要合理就可以采用。
3.本课时是在学生学习了加、减法的估算及其中一个因数是一位数的乘法估算的基础上进行教学的,本课时的学习将进一步提高学生分析问题和解决问题的能力。
备已学知识
1.用2~9的乘法口诀求商。
2.有余数的除法。
3.除数是一位数的除法。
备教学目标
知识与技能
1.掌握除数是一位数的除法的估算方法,体验估算方法的多样化。
2.能用除法估算解决简单的实际问题。
过程与方法
1.结合具体情境,找出解决问题的方法,从而培养学生解决问题的能力。
2.通过小组合作学习、主动探究等活动,培养学生的估算能力,以及与他人交流思考过程和结果的能力。
情感、态度与价值观
1.通过探究估算方法的多样化,激发学生的学习兴趣,培养学生主动探究的意识。
2.培养初步的应用意识和热爱数学的良好情感。
备重点难点
重点:掌握除数是一位数的除法的估算方法。
难点:根据具体情境合理地进行估算。
备知识讲解
知识点一 用除数是一位数的除法估算解决问题
问题导入 每天的住宿费大约是多少钱?(教材29页例8)
过程讲解
1.观图、读题,获取数学信息
(1)已知条件:一家三口在宾馆住了3天,住宿费一共是267元。
(2)所求问题:每天的住宿费大约是多少钱?
2.理解题意并列式
(1)理解关键词语:“每天的住宿费大约是多少钱”,“大约”表示所求的结果不用算出准确的钱数,只需估算出与准确结果比较接近的大致结果即可。
(2)理解题意并列式:已知3天的住宿费一共是267元,求每天的住宿费,用总钱数除以住的天数,列式为267÷3。
3.探究267÷3的估算方法
方法一 把被除数看作整百数。
267元接近300元,把267÷3看作300÷3,300÷3=100,所以267÷3≈100。
方法二 把被除数看作几百几十数。
267元接近270元,把267÷3看作270÷3,270÷3=90,所以267÷3≈90。
4.解决问题
解法一 267÷3≈100(元)
答:每天的住宿费大约是100元。
解法二 267÷3≈90(元)
答:每天的住宿费大约是90元。
[方法提示:两种估算方法虽然结果有差异,但都接近准确值,不影响对问题的合理解决。]
5.回顾反思,体会估算方法的合理性
取与267接近的数估算 结论
方法一 267≈300 300÷3= 100(元) 267<300每天的住宿费大约是100元,且比100元少。
方法二 267≈270 270÷3= 90(元) 267<270每天的住宿费大约是90元,且比90元少。
得出:解决某一个问题可以有多种估算方法,在这些估算方法中,会有一种估算方法对解决这个问题更具合理性,更接近准确结果。
[重点提示:此题精确答案比90元少,但一定比80元多。因为若每天的住宿费是80元,则3天就是240元,240<267,与题意不符,所以解决用钱问题时应估大不估小。因为结果是近似值,所以用“≈”连接。]
归纳总结
一位数除三位数的估算方法:除数不变,把被除数看作与它接近的整百数或几百几十数(能被整除),然后按整百数或几百几十数除以一位数的方法口算出结果。
知识点二 用不同的估算策略解决实际问题
问题导入 装菠萝。(教材30页例9)
过程讲解
1.观图、读题,获取数学信息
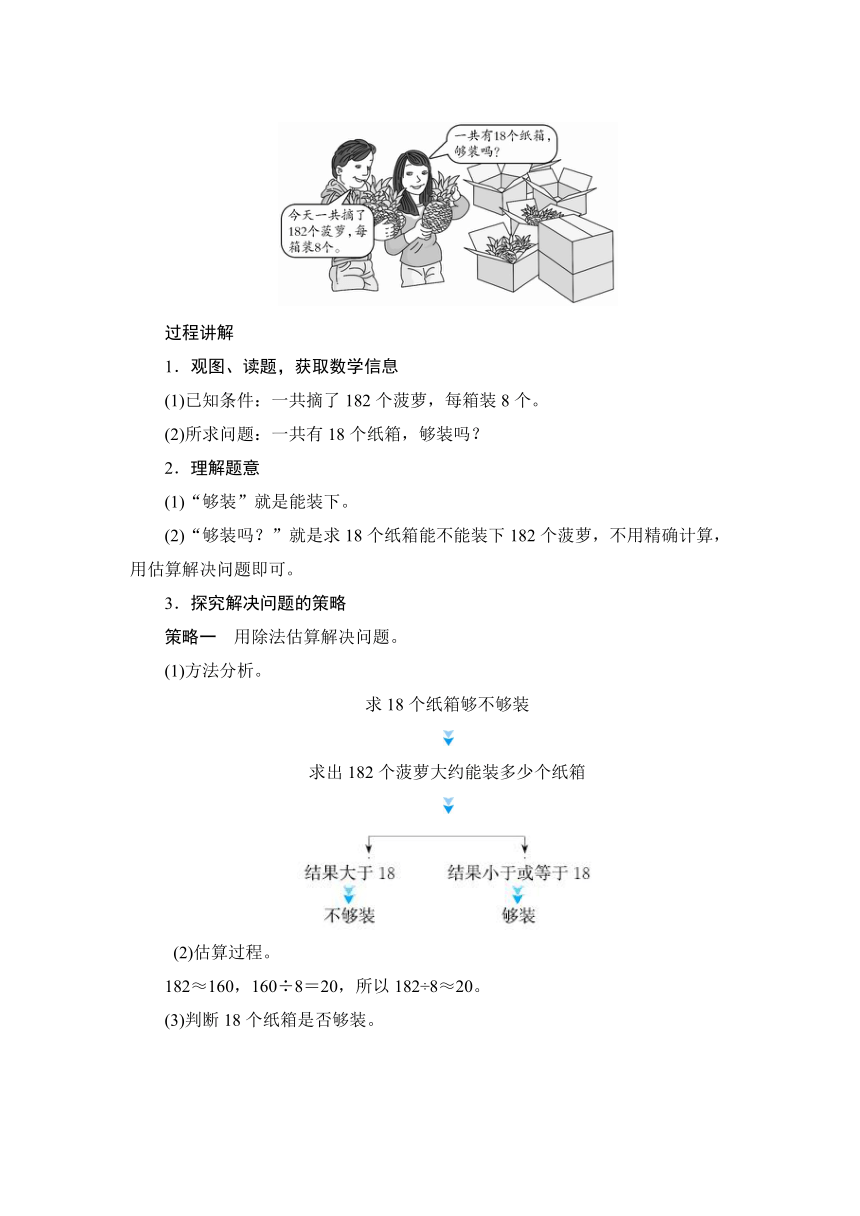
(1)已知条件:一共摘了182个菠萝,每箱装8个。
(2)所求问题:一共有18个纸箱,够装吗?
2.理解题意
(1)“够装”就是能装下。
(2)“够装吗?”就是求18个纸箱能不能装下182个菠萝,不用精确计算,用估算解决问题即可。
3.探究解决问题的策略
策略一 用除法估算解决问题。
(1)方法分析。
求18个纸箱够不够装
求出182个菠萝大约能装多少个纸箱
(2)估算过程。
182≈160,160÷8=20,所以182÷8≈20。
(3)判断18个纸箱是否够装。
182÷8>20
即装182个菠萝需要的纸箱多于20个。因此18个纸箱不够装。
策略二 用乘法估算解决问题。
(1)方法分析。
求18个纸箱够不够装
求出18个纸箱大约能装多少个菠萝
(2)估算过程。
18接近20,20×8=160,所以18×8≈160。
(3)判断18个纸箱是否够装。
小结:估算的结果有差异,但都接近准确值,不影响问题的合理解决。
4.检验估算结论的正确性
(1)检验方法:计算出准确结果,检验估算方法是否合理。
(2)检验过程:182÷8=22(个)……6(个),通过计算可以知道182个菠萝能装22个纸箱,还剩6个,这6个菠萝还要再装1个纸箱,所以装下这些菠萝至少需要23个纸箱,18个纸箱不够装。由此说明上面两种估算方法都是合理的。
归纳总结
用不同的估算策略解决实际问题时,要根据具体的问题情境灵活选择估算的方法,可以通过精确计算验证估算策略,从而得出结论的正确性。
备易错易混
误区 每瓶饮料3元,58元最多能买多少瓶饮料?
58≈60 60÷3=20(瓶)
答:58元最多能买20瓶饮料。
错解分析 此题错在没有根据生活实际合理地估算。60÷3=20(瓶),因为60元正好能买20瓶饮料,而58元比60元少2元,2元不够买1瓶饮料,所以58元最多能买19瓶饮料。
错解改正 58÷3≈19(瓶)
答:58元最多能买19瓶饮料。
温馨提示
估算是为解决生活中的实际问题而服务的,所以要联系生活实际进行估算。
备综合能力
方法运用 运用画线段图法解决差倍问题
典型例题 陈叔叔和李叔叔都是集邮爱好者,陈叔叔收集的邮票数是李叔叔的3倍,如果陈叔叔卖掉180张邮票,李叔叔卖掉30张邮票,则两人余下的邮票数就一样多。陈叔叔原来有多少张邮票?
思路分析 把李叔叔原来的邮票数看作1份数,则陈叔叔原来的邮票数就是这样的3份数。如下图所示:
陈叔叔卖掉180张,李叔叔卖掉30张:
150张对应2份,由此可先求出李叔叔原来的邮票数,即1份数,再求陈叔叔原来的邮票数,即3份数。
正确解答 (180-30)÷(3-1)=75(张)
75×3=225(张)
答:陈叔叔原来有225张邮票。
方法总结 较复杂的差倍问题数量关系比较隐蔽,可以先用画线段图法找出两个数的差以及差所对应的份数,再进行计算。
综合运用 运用列表法和消元法解决实际问题
典型例题 买1张桌子和1把椅子各需多少钱?
思路分析 由图可列表如下:
桌子(张) 椅子(把) 价钱(元)
1 2 336
1 5 540
由上表可知,①1张桌子+2把椅子=336元;②1张桌子+5把椅子=540元,用②-①可以消去一个未知量,进而可以求出1把椅子的价钱,再根据1把椅子的价钱可以求出1张桌子的价钱。
正确解答 5-2=3(把)
540-336=204(元)
1把椅子的价钱:204÷3=68(元)
1张桌子的价钱:336-68×2=200(元)
答:买1张桌子需200元,买1把椅子需68元。
方法总结 当题中有两个或两个以上的未知量时,可以先运用消元法消去一些未知量,使未知量减少到一个,求出这个未知量后,再将所求结果代入原题,逐步求出其他未知量。
备教学资料
估算的策略
1.“分部分”估计。
2. “四舍五入”法。
3. 中间数法。(32+37+30+39可以估成35×4)
4. 一个估大,一个估小。
5. 根据实际问题选择合理的估算策略。
(43×4,带200元钱够不够?把43估成50)
备教材内容
1.本课时学习的是教材29、30页的内容。
2.例8呈现了一家人住宿宾馆结账的情境,引导学生用估算解决“每天的住宿费的问题”,感受数学与日常生活的密切联系。例9创设了“用18个纸箱装菠萝够不够”的问题情境,并给出不同的解决问题的策略,使学生明确解决同一个问题可以有不同的方法,只要合理就可以采用。
3.本课时是在学生学习了加、减法的估算及其中一个因数是一位数的乘法估算的基础上进行教学的,本课时的学习将进一步提高学生分析问题和解决问题的能力。
备已学知识
1.用2~9的乘法口诀求商。
2.有余数的除法。
3.除数是一位数的除法。
备教学目标
知识与技能
1.掌握除数是一位数的除法的估算方法,体验估算方法的多样化。
2.能用除法估算解决简单的实际问题。
过程与方法
1.结合具体情境,找出解决问题的方法,从而培养学生解决问题的能力。
2.通过小组合作学习、主动探究等活动,培养学生的估算能力,以及与他人交流思考过程和结果的能力。
情感、态度与价值观
1.通过探究估算方法的多样化,激发学生的学习兴趣,培养学生主动探究的意识。
2.培养初步的应用意识和热爱数学的良好情感。
备重点难点
重点:掌握除数是一位数的除法的估算方法。
难点:根据具体情境合理地进行估算。
备知识讲解
知识点一 用除数是一位数的除法估算解决问题
问题导入 每天的住宿费大约是多少钱?(教材29页例8)
过程讲解
1.观图、读题,获取数学信息
(1)已知条件:一家三口在宾馆住了3天,住宿费一共是267元。
(2)所求问题:每天的住宿费大约是多少钱?
2.理解题意并列式
(1)理解关键词语:“每天的住宿费大约是多少钱”,“大约”表示所求的结果不用算出准确的钱数,只需估算出与准确结果比较接近的大致结果即可。
(2)理解题意并列式:已知3天的住宿费一共是267元,求每天的住宿费,用总钱数除以住的天数,列式为267÷3。
3.探究267÷3的估算方法
方法一 把被除数看作整百数。
267元接近300元,把267÷3看作300÷3,300÷3=100,所以267÷3≈100。
方法二 把被除数看作几百几十数。
267元接近270元,把267÷3看作270÷3,270÷3=90,所以267÷3≈90。
4.解决问题
解法一 267÷3≈100(元)
答:每天的住宿费大约是100元。
解法二 267÷3≈90(元)
答:每天的住宿费大约是90元。
[方法提示:两种估算方法虽然结果有差异,但都接近准确值,不影响对问题的合理解决。]
5.回顾反思,体会估算方法的合理性
取与267接近的数估算 结论
方法一 267≈300 300÷3= 100(元) 267<300每天的住宿费大约是100元,且比100元少。
方法二 267≈270 270÷3= 90(元) 267<270每天的住宿费大约是90元,且比90元少。
得出:解决某一个问题可以有多种估算方法,在这些估算方法中,会有一种估算方法对解决这个问题更具合理性,更接近准确结果。
[重点提示:此题精确答案比90元少,但一定比80元多。因为若每天的住宿费是80元,则3天就是240元,240<267,与题意不符,所以解决用钱问题时应估大不估小。因为结果是近似值,所以用“≈”连接。]
归纳总结
一位数除三位数的估算方法:除数不变,把被除数看作与它接近的整百数或几百几十数(能被整除),然后按整百数或几百几十数除以一位数的方法口算出结果。
知识点二 用不同的估算策略解决实际问题
问题导入 装菠萝。(教材30页例9)
过程讲解
1.观图、读题,获取数学信息
(1)已知条件:一共摘了182个菠萝,每箱装8个。
(2)所求问题:一共有18个纸箱,够装吗?
2.理解题意
(1)“够装”就是能装下。
(2)“够装吗?”就是求18个纸箱能不能装下182个菠萝,不用精确计算,用估算解决问题即可。
3.探究解决问题的策略
策略一 用除法估算解决问题。
(1)方法分析。
求18个纸箱够不够装
求出182个菠萝大约能装多少个纸箱
(2)估算过程。
182≈160,160÷8=20,所以182÷8≈20。
(3)判断18个纸箱是否够装。
182÷8>20
即装182个菠萝需要的纸箱多于20个。因此18个纸箱不够装。
策略二 用乘法估算解决问题。
(1)方法分析。
求18个纸箱够不够装
求出18个纸箱大约能装多少个菠萝
(2)估算过程。
18接近20,20×8=160,所以18×8≈160。
(3)判断18个纸箱是否够装。
小结:估算的结果有差异,但都接近准确值,不影响问题的合理解决。
4.检验估算结论的正确性
(1)检验方法:计算出准确结果,检验估算方法是否合理。
(2)检验过程:182÷8=22(个)……6(个),通过计算可以知道182个菠萝能装22个纸箱,还剩6个,这6个菠萝还要再装1个纸箱,所以装下这些菠萝至少需要23个纸箱,18个纸箱不够装。由此说明上面两种估算方法都是合理的。
归纳总结
用不同的估算策略解决实际问题时,要根据具体的问题情境灵活选择估算的方法,可以通过精确计算验证估算策略,从而得出结论的正确性。
备易错易混
误区 每瓶饮料3元,58元最多能买多少瓶饮料?
58≈60 60÷3=20(瓶)
答:58元最多能买20瓶饮料。
错解分析 此题错在没有根据生活实际合理地估算。60÷3=20(瓶),因为60元正好能买20瓶饮料,而58元比60元少2元,2元不够买1瓶饮料,所以58元最多能买19瓶饮料。
错解改正 58÷3≈19(瓶)
答:58元最多能买19瓶饮料。
温馨提示
估算是为解决生活中的实际问题而服务的,所以要联系生活实际进行估算。
备综合能力
方法运用 运用画线段图法解决差倍问题
典型例题 陈叔叔和李叔叔都是集邮爱好者,陈叔叔收集的邮票数是李叔叔的3倍,如果陈叔叔卖掉180张邮票,李叔叔卖掉30张邮票,则两人余下的邮票数就一样多。陈叔叔原来有多少张邮票?
思路分析 把李叔叔原来的邮票数看作1份数,则陈叔叔原来的邮票数就是这样的3份数。如下图所示:
陈叔叔卖掉180张,李叔叔卖掉30张:
150张对应2份,由此可先求出李叔叔原来的邮票数,即1份数,再求陈叔叔原来的邮票数,即3份数。
正确解答 (180-30)÷(3-1)=75(张)
75×3=225(张)
答:陈叔叔原来有225张邮票。
方法总结 较复杂的差倍问题数量关系比较隐蔽,可以先用画线段图法找出两个数的差以及差所对应的份数,再进行计算。
综合运用 运用列表法和消元法解决实际问题
典型例题 买1张桌子和1把椅子各需多少钱?
思路分析 由图可列表如下:
桌子(张) 椅子(把) 价钱(元)
1 2 336
1 5 540
由上表可知,①1张桌子+2把椅子=336元;②1张桌子+5把椅子=540元,用②-①可以消去一个未知量,进而可以求出1把椅子的价钱,再根据1把椅子的价钱可以求出1张桌子的价钱。
正确解答 5-2=3(把)
540-336=204(元)
1把椅子的价钱:204÷3=68(元)
1张桌子的价钱:336-68×2=200(元)
答:买1张桌子需200元,买1把椅子需68元。
方法总结 当题中有两个或两个以上的未知量时,可以先运用消元法消去一些未知量,使未知量减少到一个,求出这个未知量后,再将所求结果代入原题,逐步求出其他未知量。
备教学资料
估算的策略
1.“分部分”估计。
2. “四舍五入”法。
3. 中间数法。(32+37+30+39可以估成35×4)
4. 一个估大,一个估小。
5. 根据实际问题选择合理的估算策略。
(43×4,带200元钱够不够?把43估成50)
