人教版数学二年级下册 第5单元第3课时《解决问题》教案
文档属性
| 名称 | 人教版数学二年级下册 第5单元第3课时《解决问题》教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 597.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 08:51:54 | ||
图片预览

文档简介
第3课时 解决问题
备教材内容
1.本课时学习的是教材53、54页的内容及相关习题。
2.例4教学需要用两步计算解决简单实际问题,教材用烤面包的情境提供了现实素材。目的是使学生在理解图意的基础上,发现问题、提出问题,同时结合已知条件分析问题,为后面列式解决问题奠定基础。
备已学知识
连续两问应用题的解题方法:解答第二个问题时需要将第一个问题的解答结果作为第二个问题的一个已知条件。
备教学目标
知识与技能
1.学会用色条图(线段图的雏形)分析数量关系,渗透数形结合思想,丰富解决问题的策略。
2.在分步列式解决问题的基础上,逐步学会列综合算式解决问题,会合理运用小括号改变运算顺序。
过程与方法
经历从生活中发现问题、提出问题和解决问题的过程,学会用找中间问题的方法解决两步计算应用题,丰富学生解决问题的策略。
情感、态度与价值观
在解决实际问题的过程中,体会数学在日常生活中的应用,培养学生认真观察、独立思考、合作交流等良好的学习习惯,激发学习数学的兴趣。
备重点难点
重点:利用色条图分析数量关系,掌握解决两步计算应用题的方法。
难点:能找出隐藏的中间问题,合理利用小括号列综合算式解决问题。
备知识讲解
知识点 用两步计算解决问题(掌握运用)
问题导入 剩下的还要烤几次?(教材53页例4)
过程讲解
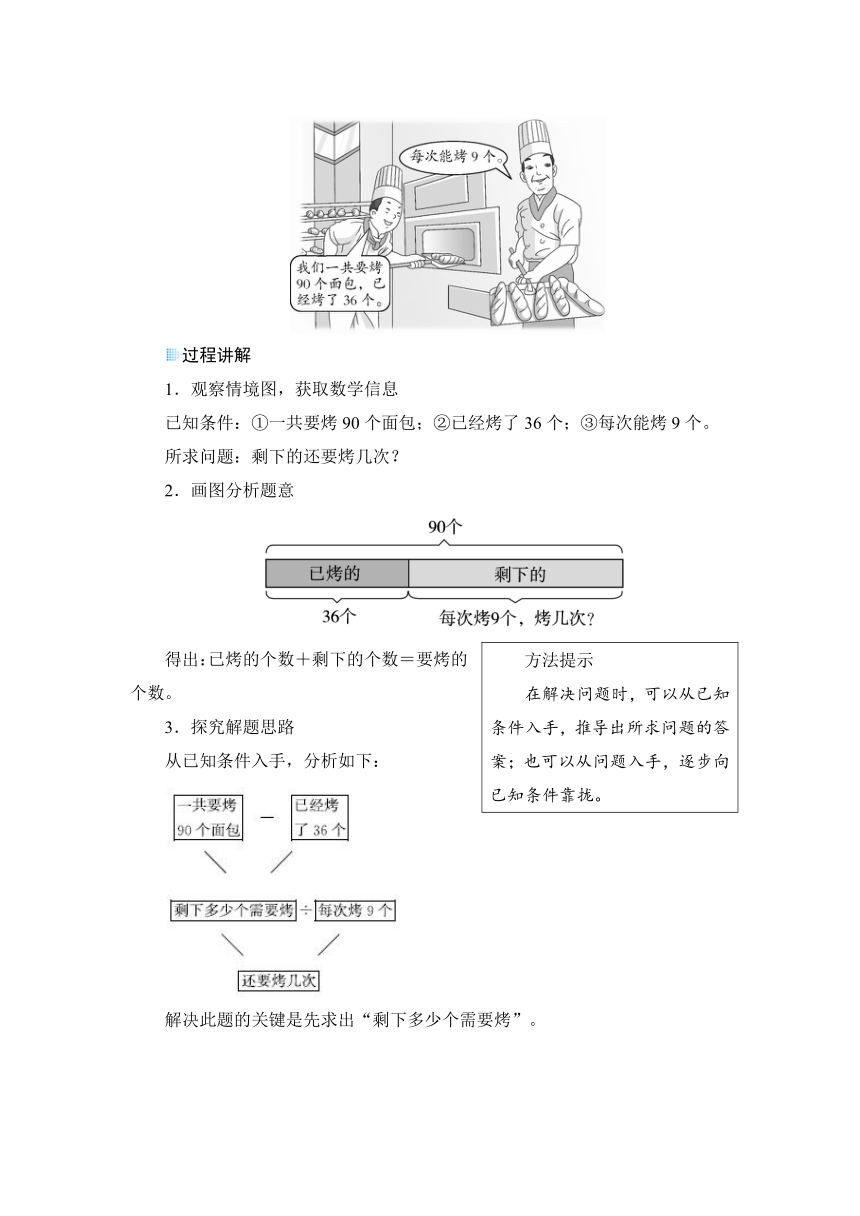
1.观察情境图,获取数学信息
已知条件:①一共要烤90个面包;②已经烤了36个;③每次能烤9个。
所求问题:剩下的还要烤几次?
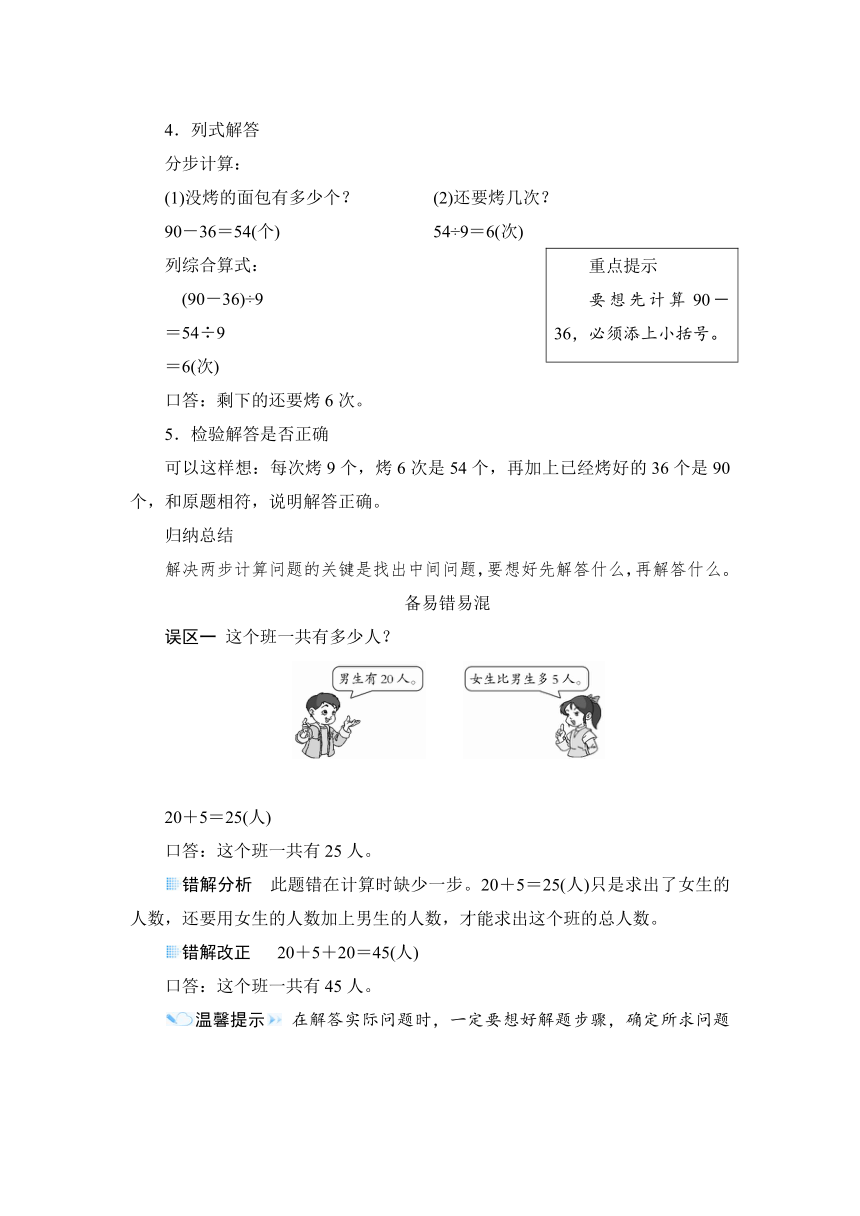
2.画图分析题意
方法提示 在解决问题时,可以从已知条件入手,推导出所求问题的答案;也可以从问题入手,逐步向已知条件靠拢。
得出:已烤的个数+剩下的个数=要烤的个数。
3.探究解题思路
从已知条件入手,分析如下:
解决此题的关键是先求出“剩下多少个需要烤”。
4.列式解答
分步计算:
(1)没烤的面包有多少个? (2)还要烤几次?
90-36=54(个) 54÷9=6(次)
重点提示 要想先计算90-36,必须添上小括号。
列综合算式:
(90-36)÷9
=54÷9
=6(次)
口答:剩下的还要烤6次。
5.检验解答是否正确
可以这样想:每次烤9个,烤6次是54个,再加上已经烤好的36个是90个,和原题相符,说明解答正确。
归纳总结
解决两步计算问题的关键是找出中间问题,要想好先解答什么,再解答什么。
备易错易混
误区一 这个班一共有多少人?
20+5=25(人)
口答:这个班一共有25人。
错解分析 此题错在计算时缺少一步。20+5=25(人)只是求出了女生的人数,还要用女生的人数加上男生的人数,才能求出这个班的总人数。
错解改正 20+5+20=45(人)
口答:这个班一共有45人。
温馨提示 在解答实际问题时,一定要想好解题步骤,确定所求问题需要几步来完成。
误区二 张奶奶家养了4只黑兔,8只白兔,把这些兔子平均放在4个笼子里,每个笼子放几只?
4+8÷4
=4+2
=6(只)
口答:每个笼子放6只。
错解分析 此题错在列综合算式时没有使用小括号。这道题应先用加法求出黑兔和白兔一共有多少只,再用除法求出每个笼子放几只。所以在列综合算式时,要把4+8用小括号括起来,才能保证第一步算加法。
错解改正 (4+8)÷4
=12÷4
=3(只)
口答:每个笼子放3只。
温馨提示 在列综合算式解答实际问题时,一定要注意小括号的使用。
备综合能力
能力点一 运用画直观图法解决和倍问题
典型例题 龙龙今年8岁,妈妈的年龄比龙龙年龄的4倍还多2岁。妈妈比龙龙大多少岁?
思路分析 龙龙和妈妈的年龄关系如下图所示:
思路一 要求妈妈比龙龙大多少岁,可以先求出妈妈的年龄。根据图意,能用“乘加”求出妈妈的年龄,再用减法求出妈妈比龙龙大多少岁。
思路二 妈妈的年龄比龙龙年龄的4倍还多2岁,如果把龙龙的年龄看作1份,那么妈妈的年龄就是4份加2岁,比龙龙大4-1=3(份)零2岁。
正确解答 方法一 8×4+2=34(岁)
34-8=26(岁)
方法二 4-1=3 8×3+2=26(岁)
口答:妈妈比龙龙大26岁。
方法提示 解决此类问题时,可以利用直观图帮助分析数量关系,理清思路。
能力点二 运用抓不变量法解决复杂的乘减问题
典型例题 二(1)班的同学排队做操,如果每行排6人,排成5行还缺2人。如果每行排5人,排成5行,还余下多少人?
思路分析 不管怎样排队,总人数是不变的。根据“每行排6人,排成5行还缺2人”可以求出二(1)班共有多少人,再根据“每行排5人,排成5行”可以求出重新排队时这5行的人数,最后从总人数中去掉重新排队时这5行的人数,就是余下的人数。
正确解答 6×5-2=28(人)
28-5×5=3(人)
口答:还余下3人。
方法提示 解决此类问题时,找出题中的不变量是解题关键。
备教学资料
小学应用题教学的演变
从建国到1965年。当时的算术课程十分重视应用题,1956年《小学算术教学大纲(修订草案)》中规定:应当用算术课和算术课以外作业总时间的一半左右来解答应用题。同时把应用题按苏联的经验分为“简单”“复合”和“典型”三大类,每一大类又细分为很多类型。1963年《全日制小学算术教学大纲(草案)》将简单应用题分为12种,复合应用题学到2~5步,典型应用题多达十余种。
1978年制定了《全日制十年制学校小学数学教学大纲(试行草案)》。《大纲》明确指出:使学生能够运用所学的知识解决日常生产、生活中的简单的实际问题。并将“小学算术”易名为“小学数学”,在小学数学中正式引入方程,大大缩短了人们的认识历程。在以后的二十年中,一步应用题不再人为分类,复合应用题也只学到4步,典型应用题也大幅度地简化。应用题的老大难问题得到一定程度地缓解,小学生解决问题的能力也有了提高。
备教材内容
1.本课时学习的是教材53、54页的内容及相关习题。
2.例4教学需要用两步计算解决简单实际问题,教材用烤面包的情境提供了现实素材。目的是使学生在理解图意的基础上,发现问题、提出问题,同时结合已知条件分析问题,为后面列式解决问题奠定基础。
备已学知识
连续两问应用题的解题方法:解答第二个问题时需要将第一个问题的解答结果作为第二个问题的一个已知条件。
备教学目标
知识与技能
1.学会用色条图(线段图的雏形)分析数量关系,渗透数形结合思想,丰富解决问题的策略。
2.在分步列式解决问题的基础上,逐步学会列综合算式解决问题,会合理运用小括号改变运算顺序。
过程与方法
经历从生活中发现问题、提出问题和解决问题的过程,学会用找中间问题的方法解决两步计算应用题,丰富学生解决问题的策略。
情感、态度与价值观
在解决实际问题的过程中,体会数学在日常生活中的应用,培养学生认真观察、独立思考、合作交流等良好的学习习惯,激发学习数学的兴趣。
备重点难点
重点:利用色条图分析数量关系,掌握解决两步计算应用题的方法。
难点:能找出隐藏的中间问题,合理利用小括号列综合算式解决问题。
备知识讲解
知识点 用两步计算解决问题(掌握运用)
问题导入 剩下的还要烤几次?(教材53页例4)
过程讲解
1.观察情境图,获取数学信息
已知条件:①一共要烤90个面包;②已经烤了36个;③每次能烤9个。
所求问题:剩下的还要烤几次?
2.画图分析题意
方法提示 在解决问题时,可以从已知条件入手,推导出所求问题的答案;也可以从问题入手,逐步向已知条件靠拢。
得出:已烤的个数+剩下的个数=要烤的个数。
3.探究解题思路
从已知条件入手,分析如下:
解决此题的关键是先求出“剩下多少个需要烤”。
4.列式解答
分步计算:
(1)没烤的面包有多少个? (2)还要烤几次?
90-36=54(个) 54÷9=6(次)
重点提示 要想先计算90-36,必须添上小括号。
列综合算式:
(90-36)÷9
=54÷9
=6(次)
口答:剩下的还要烤6次。
5.检验解答是否正确
可以这样想:每次烤9个,烤6次是54个,再加上已经烤好的36个是90个,和原题相符,说明解答正确。
归纳总结
解决两步计算问题的关键是找出中间问题,要想好先解答什么,再解答什么。
备易错易混
误区一 这个班一共有多少人?
20+5=25(人)
口答:这个班一共有25人。
错解分析 此题错在计算时缺少一步。20+5=25(人)只是求出了女生的人数,还要用女生的人数加上男生的人数,才能求出这个班的总人数。
错解改正 20+5+20=45(人)
口答:这个班一共有45人。
温馨提示 在解答实际问题时,一定要想好解题步骤,确定所求问题需要几步来完成。
误区二 张奶奶家养了4只黑兔,8只白兔,把这些兔子平均放在4个笼子里,每个笼子放几只?
4+8÷4
=4+2
=6(只)
口答:每个笼子放6只。
错解分析 此题错在列综合算式时没有使用小括号。这道题应先用加法求出黑兔和白兔一共有多少只,再用除法求出每个笼子放几只。所以在列综合算式时,要把4+8用小括号括起来,才能保证第一步算加法。
错解改正 (4+8)÷4
=12÷4
=3(只)
口答:每个笼子放3只。
温馨提示 在列综合算式解答实际问题时,一定要注意小括号的使用。
备综合能力
能力点一 运用画直观图法解决和倍问题
典型例题 龙龙今年8岁,妈妈的年龄比龙龙年龄的4倍还多2岁。妈妈比龙龙大多少岁?
思路分析 龙龙和妈妈的年龄关系如下图所示:
思路一 要求妈妈比龙龙大多少岁,可以先求出妈妈的年龄。根据图意,能用“乘加”求出妈妈的年龄,再用减法求出妈妈比龙龙大多少岁。
思路二 妈妈的年龄比龙龙年龄的4倍还多2岁,如果把龙龙的年龄看作1份,那么妈妈的年龄就是4份加2岁,比龙龙大4-1=3(份)零2岁。
正确解答 方法一 8×4+2=34(岁)
34-8=26(岁)
方法二 4-1=3 8×3+2=26(岁)
口答:妈妈比龙龙大26岁。
方法提示 解决此类问题时,可以利用直观图帮助分析数量关系,理清思路。
能力点二 运用抓不变量法解决复杂的乘减问题
典型例题 二(1)班的同学排队做操,如果每行排6人,排成5行还缺2人。如果每行排5人,排成5行,还余下多少人?
思路分析 不管怎样排队,总人数是不变的。根据“每行排6人,排成5行还缺2人”可以求出二(1)班共有多少人,再根据“每行排5人,排成5行”可以求出重新排队时这5行的人数,最后从总人数中去掉重新排队时这5行的人数,就是余下的人数。
正确解答 6×5-2=28(人)
28-5×5=3(人)
口答:还余下3人。
方法提示 解决此类问题时,找出题中的不变量是解题关键。
备教学资料
小学应用题教学的演变
从建国到1965年。当时的算术课程十分重视应用题,1956年《小学算术教学大纲(修订草案)》中规定:应当用算术课和算术课以外作业总时间的一半左右来解答应用题。同时把应用题按苏联的经验分为“简单”“复合”和“典型”三大类,每一大类又细分为很多类型。1963年《全日制小学算术教学大纲(草案)》将简单应用题分为12种,复合应用题学到2~5步,典型应用题多达十余种。
1978年制定了《全日制十年制学校小学数学教学大纲(试行草案)》。《大纲》明确指出:使学生能够运用所学的知识解决日常生产、生活中的简单的实际问题。并将“小学算术”易名为“小学数学”,在小学数学中正式引入方程,大大缩短了人们的认识历程。在以后的二十年中,一步应用题不再人为分类,复合应用题也只学到4步,典型应用题也大幅度地简化。应用题的老大难问题得到一定程度地缓解,小学生解决问题的能力也有了提高。
