华师大版八年级上册13.5.3角平分线 课件(共21张PPT)
文档属性
| 名称 | 华师大版八年级上册13.5.3角平分线 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1014.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 09:34:01 | ||
图片预览




文档简介
(共22张PPT)
13.5.3
“严格性之于数学家,
犹如道德之于人”
-----韦伊
要在一个三角形居住区内修一个幼儿园M,使得M到AB、BC、CA这三条公路的距离都相等,请在三角形居住区内标出幼儿园M的位置,M在何处?
A
B
C
情境导入
1、探索并证明角平分线性质定理及其逆定理,并能简单运用;
2、经历观察、猜想、验证的探究过程,进一步发展归纳和推理能力。
3、感受类比的学习方法,提高分析问题和解决问题的能力.
问题一:
1、画图:①在图中作出∠AOB的平分线OC
②在OC上任意取一点P,过点P作 PD⊥OA,PE⊥OB,垂足分别为D、E.
2、度量:量一量PD、PE的长,你能发现什么?
改变点P的位置,重复上述操作.
刚才的发现还成立吗?
3、猜想:通过上述操作,你发现了什么结论?
请用一句话概括你的发现
O
A
B
学习探究
E
D
P
A
O
B
C
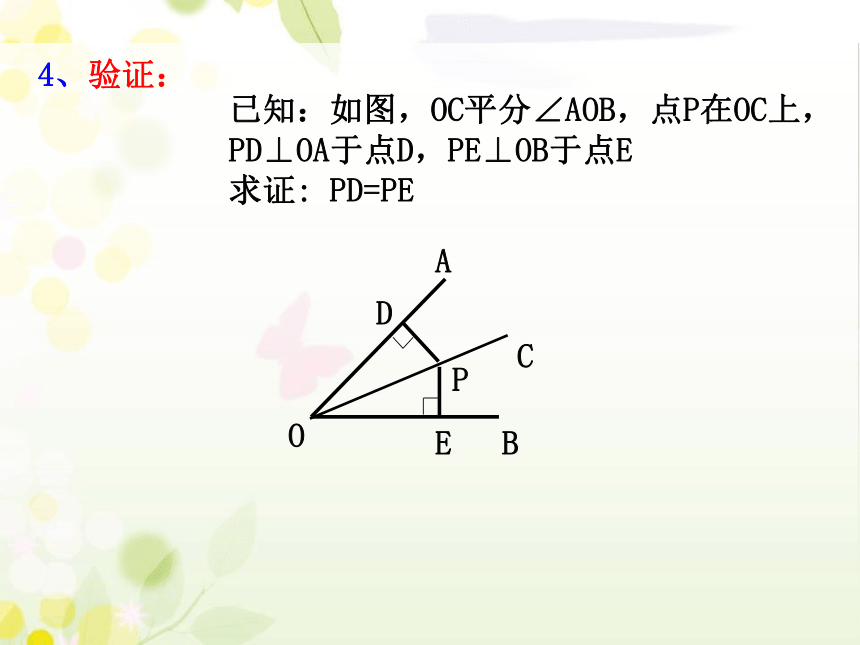
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
4、验证:
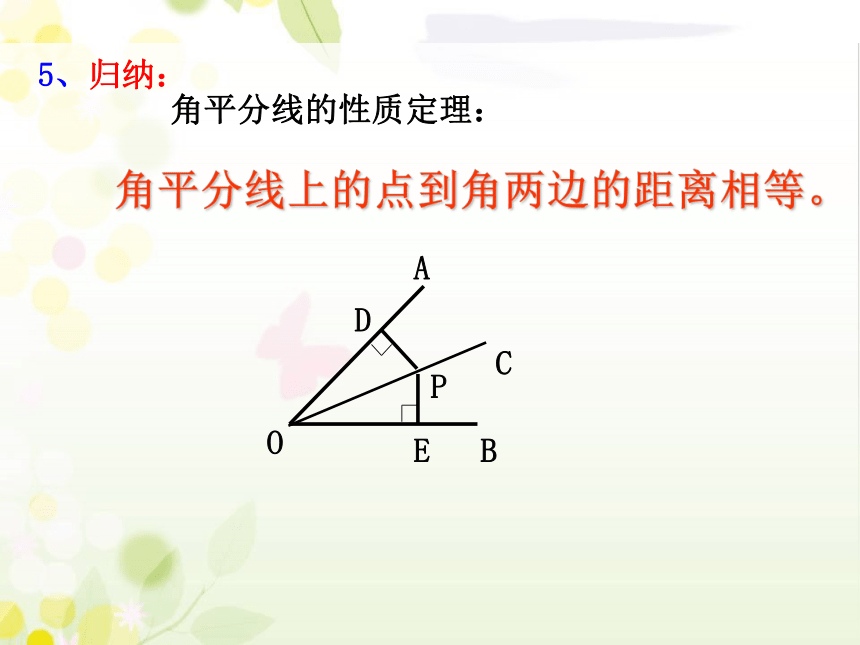
角平分线的性质定理:
角平分线上的点到角两边的距离相等。
5、归纳:
E
D
P
A
O
B
C
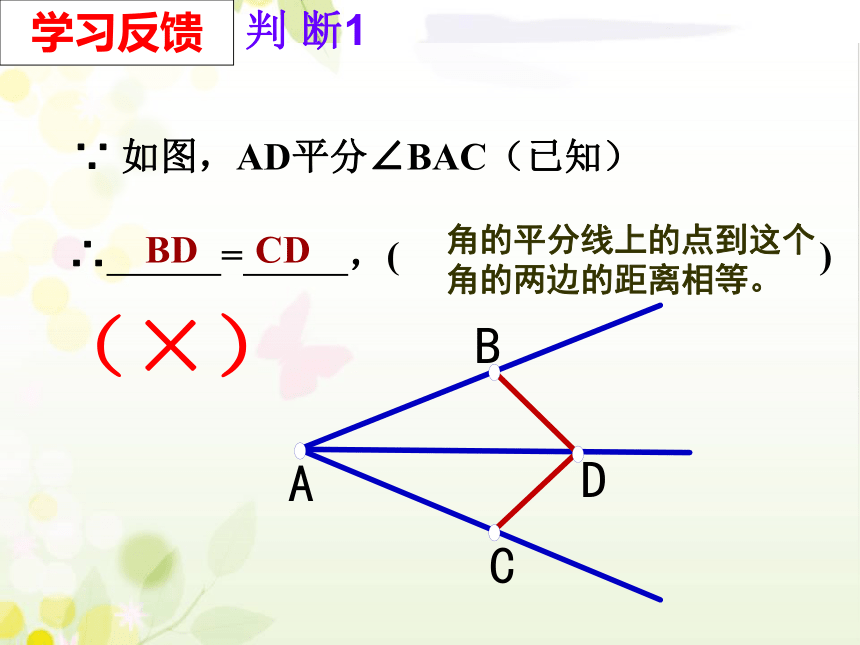
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
学习反馈
判 断1
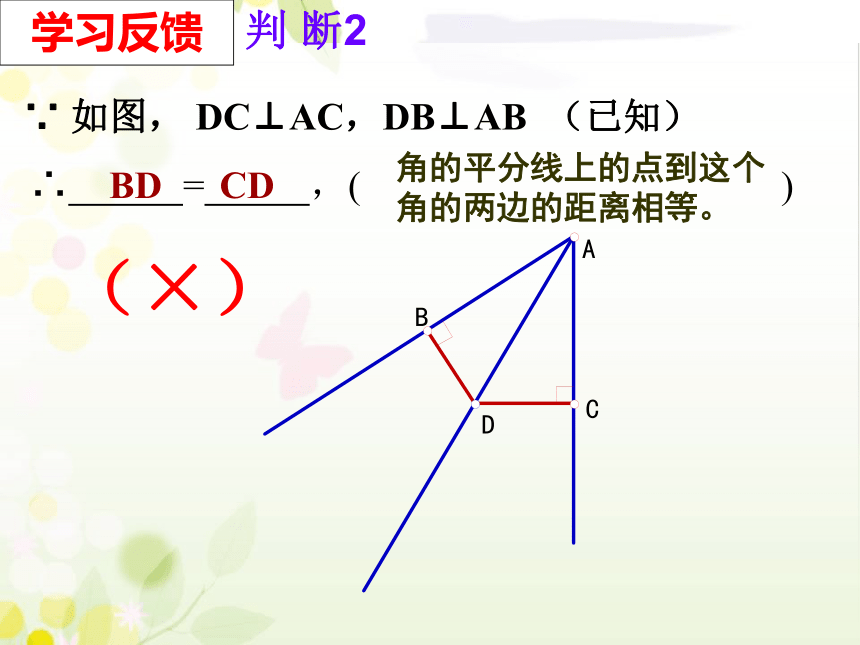
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
判 断2
学习反馈
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角的平分线上的点到这个角的两边的距离相等。
√
两个条件,
缺一不可。
判 断3
学习反馈
已知:如图,点E是∠AOB的平分线上一点, EC⊥OA,ED⊥OB,垂足分别为C、D。
求证:∠ECD=∠EDC
学习反馈
不必再证全等
条件
结论
性质定理
逆命题
一个点在角的
平分线上
这个点到角
两条边的距离
相等
角内某一点到
这个角两边的
距离相等
这个点在这个角
的平分线上
问题二:分析角平分线性质定理的条件和结论,思考它的逆命题的条件和结论,完成下表。
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,且PD=PE.
求证:点P在∠AOB 的平分线上.
证明: 过点O、P作射线OP
∵PD⊥OA,PE⊥OB,
在Rt △PDO 与Rt △PEO中
∴∠PDO= ∠PEO=900
∴Rt△PDO≌ Rt △PDO(H.L.)
∴∠1=∠2 即点P在∠AOB的平分线上
角平分线上的点到角两边的距离相等。
逆命题
角的内部到角两边的距离相等的点在角的平分线上.
A
O
B
P
D
E
PD=PE(已知)
OP=OP(公共边)
逆定理
角的内部到角两边距离相等的点在角的平分线上。
A
O
B
P
D
E
C
2、已知:在△ABC中,AD平分∠BAC,
BE平分∠ABC,AD和BE相交于点O 。
求证:点O在∠ACB的平分线上。
学习反馈
F
G
H
I
在一个三角形居住区内修有一个幼儿园M,M到AB、BC、CA三边的距离都相等,请在三角形居住区内标出M的位置,M在何处?
A
B
C
解决问题
M
∴ M点位于△ABC三条角平分线的交点处
三角形内到三边距离相等的点是三条角平分线的交点。
感悟与收获
2.通过本节课的学习,你有什么收获?
1.本节课我们学习了哪些知识?
如图,已知点C是射线OP上的一点,点D、E分别在OA、OB上,且CD⊥OA,CE ⊥ OB,______________(添加一个条件)。
使得CD=CE。
A
O
B
C
D
E
P
请运用今天所学的知识,在此题中完成条件添加,考考你的同桌。
∠AOP= ∠BOP
练习巩固
如图,在△ABC中,∠A=90°,BD是∠ABC的平分线,BC=10,AD=3,则△DBC的面积是_______
练习巩固
拓展与延伸
2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
P1
P2
P3
P4
l1
l2
l3
13.5.3
“严格性之于数学家,
犹如道德之于人”
-----韦伊
要在一个三角形居住区内修一个幼儿园M,使得M到AB、BC、CA这三条公路的距离都相等,请在三角形居住区内标出幼儿园M的位置,M在何处?
A
B
C
情境导入
1、探索并证明角平分线性质定理及其逆定理,并能简单运用;
2、经历观察、猜想、验证的探究过程,进一步发展归纳和推理能力。
3、感受类比的学习方法,提高分析问题和解决问题的能力.
问题一:
1、画图:①在图中作出∠AOB的平分线OC
②在OC上任意取一点P,过点P作 PD⊥OA,PE⊥OB,垂足分别为D、E.
2、度量:量一量PD、PE的长,你能发现什么?
改变点P的位置,重复上述操作.
刚才的发现还成立吗?
3、猜想:通过上述操作,你发现了什么结论?
请用一句话概括你的发现
O
A
B
学习探究
E
D
P
A
O
B
C
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
4、验证:
角平分线的性质定理:
角平分线上的点到角两边的距离相等。
5、归纳:
E
D
P
A
O
B
C
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
学习反馈
判 断1
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
判 断2
学习反馈
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角的平分线上的点到这个角的两边的距离相等。
√
两个条件,
缺一不可。
判 断3
学习反馈
已知:如图,点E是∠AOB的平分线上一点, EC⊥OA,ED⊥OB,垂足分别为C、D。
求证:∠ECD=∠EDC
学习反馈
不必再证全等
条件
结论
性质定理
逆命题
一个点在角的
平分线上
这个点到角
两条边的距离
相等
角内某一点到
这个角两边的
距离相等
这个点在这个角
的平分线上
问题二:分析角平分线性质定理的条件和结论,思考它的逆命题的条件和结论,完成下表。
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,且PD=PE.
求证:点P在∠AOB 的平分线上.
证明: 过点O、P作射线OP
∵PD⊥OA,PE⊥OB,
在Rt △PDO 与Rt △PEO中
∴∠PDO= ∠PEO=900
∴Rt△PDO≌ Rt △PDO(H.L.)
∴∠1=∠2 即点P在∠AOB的平分线上
角平分线上的点到角两边的距离相等。
逆命题
角的内部到角两边的距离相等的点在角的平分线上.
A
O
B
P
D
E
PD=PE(已知)
OP=OP(公共边)
逆定理
角的内部到角两边距离相等的点在角的平分线上。
A
O
B
P
D
E
C
2、已知:在△ABC中,AD平分∠BAC,
BE平分∠ABC,AD和BE相交于点O 。
求证:点O在∠ACB的平分线上。
学习反馈
F
G
H
I
在一个三角形居住区内修有一个幼儿园M,M到AB、BC、CA三边的距离都相等,请在三角形居住区内标出M的位置,M在何处?
A
B
C
解决问题
M
∴ M点位于△ABC三条角平分线的交点处
三角形内到三边距离相等的点是三条角平分线的交点。
感悟与收获
2.通过本节课的学习,你有什么收获?
1.本节课我们学习了哪些知识?
如图,已知点C是射线OP上的一点,点D、E分别在OA、OB上,且CD⊥OA,CE ⊥ OB,______________(添加一个条件)。
使得CD=CE。
A
O
B
C
D
E
P
请运用今天所学的知识,在此题中完成条件添加,考考你的同桌。
∠AOP= ∠BOP
练习巩固
如图,在△ABC中,∠A=90°,BD是∠ABC的平分线,BC=10,AD=3,则△DBC的面积是_______
练习巩固
拓展与延伸
2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
P1
P2
P3
P4
l1
l2
l3
